Angular Momentum Compared to Linear Momentum: Difference between revisions
Clindbeck3 (talk | contribs) m (→Connectedness: changed to bullet point) |
|||
| (46 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Claimed by clindbeck3 (Christopher Lindbeck) for Spring 2018 | |||
Is currently a work in progress, in heavy flux April 18th 2018. | |||
I believe there may be a solid argument for moving the contents of this page onto another page as a top level section. When it comes down to it we usually talk about angular momentum in relation to linear momentum anyway so it is difficult for this page to not just redefine angular momentum. | |||
==The Main Idea== | ==The Main Idea== | ||
Linear momentum | Linear momentum tends to behave fairly intuitively, but angular momentum has some more obtuse properties that can make it behave in less immediately intuitive ways. While many of the equations describing angular momentum look almost identical to those describing linear momentum, variables that were fixed in linear momentum can change based on multiple factors, this can lead to less intuitive behavior. In addition, angular momentum has two separate components, one of which is relative to a point of reference. | ||
Linear momentum is relatively simple, it depends upon the mass and velocity of an object, and to an extent the equation for angular momentum mimics the equation for linear momentum, but angular momentum draws a relationship between mass, velocity, AND the radius from the axis to the mass about which it is rotating. Now that your motion is relative to an axis, all of a sudden WHERE your mass is in relation to that axis MATTERS, and so the radius wriggles its way into the equations for linear motion, which makes these new equations have similar form but function in a completely different way. | Linear momentum is relatively simple, it depends upon the mass and velocity of an object, and to an extent the equation for angular momentum mimics the equation for linear momentum, but angular momentum draws a relationship between mass, velocity, AND the radius from the axis to the mass about which it is rotating. Now that your motion is relative to an axis, all of a sudden WHERE your mass is in relation to that axis MATTERS, and so the radius wriggles its way into the equations for linear motion, which makes these new equations have similar form but function in a completely different way. | ||
==A Mathematical Model== | |||
Just like there are simple equations to describe linear momentum there are equally simple equations for describing angular momentum, many of which are extremely similar. What we will come to find however is that some of the variables and factors that we take for granted with linear motion become more complex in angular motion. | |||
For example in a linearly moving system, there is only one type of movement (translational motion), and so it is relatively simple to calculate the momentum of single objects or the momentum of a system which would just be the addition of the momentum for each part. | |||
===Linear Momentum vs Angular Momentum Equations=== | |||
We can see that a number of equations look very similar with variables swapping out for one another one-for-one in equations. | |||
{| class="wikitable" | |||
! Linear Motion !! Angular (Rotational) Motion | |||
|- | |||
| Linear Position: <math>x</math> (m) | |||
| Angular Position: <math>θ</math> (rad) | |||
|- | |||
|Linear Velocity: <math>v</math> (m/s) | |||
|Angular Velocity: <math>ω</math> (rad/s) | |||
|- | |||
|Linear Motion: <math>x=\vec{v}t</math> | |||
|Angular Rotation: <math>θ=ωt</math> | |||
|- | |||
|Mass: <math>m</math> (kg) | |||
|Moment of Inertia: <math>I</math> (kg m^2) | |||
|- | |||
|Momentum: <math>p=m\vec{v}</math> | |||
|Angular Momentum: <math>\vec{L}_{rot}=I\vec{ω}</math> | |||
|- | |||
|Linear Kinetic Energy: <math>\frac{1}{2} m v^2</math> | |||
|Rotational Kinetic Energy: <math>\frac{1}{2} I ω^2</math> | |||
|} | |||
Keeping in mind that we are primarily looking at rotational angular momentum right now, lets take a look at some of the differences between the two. | |||
ω is fairly similar to linear velocity in most respects. The faster something is spinning the more radians it covers per second and the higher the ω value will be. <math>I</math> is another matter though, unlike its linear cousin <math>m</math> it is not a simple unit; Its formula is kg m^2. Moment of Inertia is different from mass in that it depends on weight distribution and axis of rotation, meaning that not only is it different for different in different motions of the same object, it can actually change during motion. These factors are what gives angular momentum its less intuitive properties. | |||
When looking at linear momentum a lot of things are simplified in the fact that mass is constant and easily measurable, but Moment of Inertia is neither of those things and this can mess with our calculations and our mental model of motion. The in-class demonstrations regarding the spinning chair and the rolling cylinders demonstrate this property. Since moment of Inertia can change, objects can change behavior without any external force acting on them by changing shape. The classic example of this is the ice skater tucking in their limbs to achieve high rotational speeds seemingly by magic. They can also seemingly float in the air defying gravity in the case of a gyroscope, or have bizarre behavior without external interaction like the [https://www.youtube.com/watch?v=1n-HMSCDYtM T-handle in space rotating back and forth]. | |||
Another major difference between linear and angular momentum is that it has two components, Rotational and Transnational. Transnational angular momentum is different from linear momentum primarily in that it differs based on a point of reference. This can be seen in the fact that it exists as the cross product of two vectors, a position vector relative to a point of reference, and the linear momentum vector. | |||
One of the other elements that we don't typically have to worry about when dealing with linear momentum that comes up in angular momentum is the direction of the momentum vector. With linear momentum it is almost always obvious which direction the momentum is heading, as it is the same direction that the object is heading. With angular momentum we need to use the right hand rule or the cross product to figure out the direction of the momentum vector. | |||
<math>L = r x p</math> | |||
This cross product is what determines the direction that the angular momentum vector faces, it is also what relates the linear momentum vector to the angular momentum vector. The two vectors form a plane and you know that the angular momentum vector will be orthogonal to that plane due to the nature of the cross product. You can use the right hand rule to figure out which direction that will be in and in many situations will not need to work out the entire cross product. | |||
Like linear momentum angular momentum has a conservation rule. Where linear momentum will not change unless an external force is applied, angular momentum will not change unless an external torque is applied. Torque is essentially the force analog for angular momentum, it causes changes to angular momentum where force causes changes in linear momentum. Torque has the unit N m because that is what it is, a force applied over a radius. Torque is not to be confused with work, for which the formula is also N m. | |||
===Direction And the Right Hand Rule=== | |||
While the direction of linear momentum is rarely difficult to deduce, the direction of angular momentum can often be less intuitive than simply the direction of motion. We use the right hand rule and the cross product with the position vector to figure out what direction our angular momentum vectors should be pointing. | |||
However in a rotational system, we have two different subcategories for angular momentum: translational and rotational. Translational angular momentum depends upon a part's component of momentum that is orthogonal to the radius from a point of reference. Rotational angular momentum depends upon the moment of inertia of each part and how fast it rotates around its own axis, so the point of reference does not play a part in rotational angular momentum (unless the object you are calculating for is | However in a rotational system, we have two different subcategories for angular momentum: translational and rotational. Translational angular momentum depends upon a part's component of momentum that is orthogonal to the radius from a point of reference. Rotational angular momentum depends upon the moment of inertia of each part and how fast it rotates around its own axis, so the point of reference does not play a part in rotational angular momentum (unless the object you are calculating for is coincidentally spinning around that exact point). | ||
# Rotational angular momentum: <math> \vec{L}_{rot} = I\vec{ω} </math> | # Rotational angular momentum: <math> \vec{L}_{rot} = I\vec{ω} </math> | ||
| Line 24: | Line 73: | ||
Glowscript Link: https://trinket.io/glowscript/239aa4fac7 | Glowscript Link: https://trinket.io/glowscript/239aa4fac7 | ||
In this model | In this model there is a very simple orbit of a spacecraft around Earth while the Moon also rotates around Earth. Trails have been left out for efficiency. From this model you can observe both linear and angular momentum. When the spacecraft comes near to the Earth, its velocity increases, and you can see this in the vectors represented by arrows. This is because <math> \vec{v} = \vec{ω}*r </math>, therefore <math> \vec{ω} </math> has increased by this formula. All of the forces on the spacecraft are from within the system and so momentum must be conserved. Now, what is the only way to increase your <math> \vec{ω} </math> in a system where momentum is conserved and there are no outside forces? Looking at the previous equations, the only way to do this is to decrease <math> \vec{I} </math>. This can be verified by observing that the spacecraft has indeed moved closer to Earth! | ||
==Examples== | ==Examples== | ||
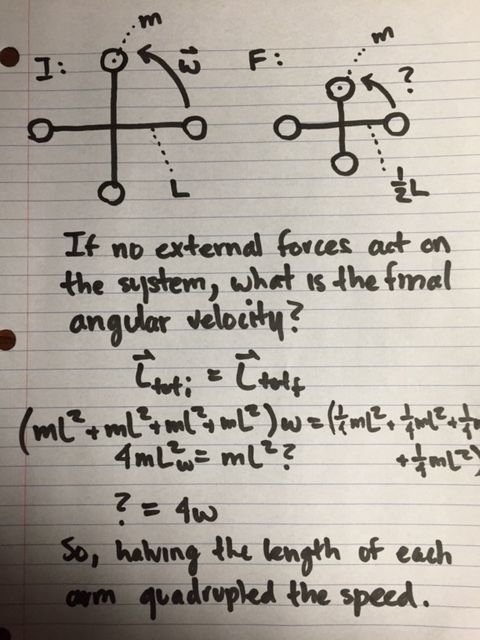
===Simple=== | |||
[[File:IMG_0800.JPG]] | |||
===Middling=== | ===Middling=== | ||
[[File:IMG_0801.JPG]] | |||
===Difficult=== | ===Difficult=== | ||
[[File:hardQuestion.jpg]] | |||
==Connectedness== | ==Connectedness== | ||
* Connection with Mathematics Curriculum | |||
** In multivariable calculus, there is an operation called the cross product, which can be easily derived from the dot product, that can give you some strange things. If you take the magnitude you get the area of a paralellogram, but more relevant to this section if you do not take the magnitude you get a vector orthogonal to the vectors you used in the cross product. There are two vectors that can be orthogonal to two other vectors if those two other vectors span a plane, both have the same magnitude but opposite directions. Which vector you use first in the cross product determines which of these two vectors is your answer, and thus the right hand rule was formed as a shortcut for an easy answer. The operation that you do in determining the cross product actually comes from determinants of matrices from linear algebra which help in determining properties of a matrix or the area of a paralellopipid created by the vectors that make the columns of that matrix. So, this operation was originally utilized for matrices and has now intertwined with physics for angular momentum and torque. | |||
*Interesting Applications | |||
** One of the most interesting things about angular momentum is that you can change <math> \vec{I} </math> and <math> \vec{ω} </math> without adding an external force which you cannot do with linear momentum (because <math> m </math> can never change internally, but <math> I </math> can). Angular momentum is used heavily in engineering and especially in dynamics. Anytime there are objects interacting with one another in the real world there will be angular momentum involved. If you want to model the motion of an holonomic robotic platform for example, the torque that each wheel exhibits on the chassis as well as the current angular momentum are very important to getting good motion. | |||
**In many applications using angular momentum instead of linear momentum makes more sense and streamlines calculations. Since you can always convert linear momentum into angular momentum by taking the cross product with the position vector you can get rid of all linear momentum vectors and deal exclusively with angular momentum, which may suit systems with lots of rotating components or an central point of reference better than working with linear momentum. | |||
==History== | ==History== | ||
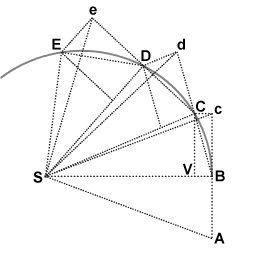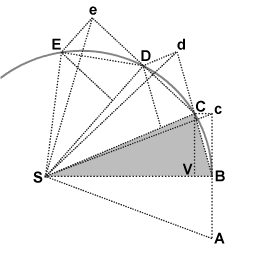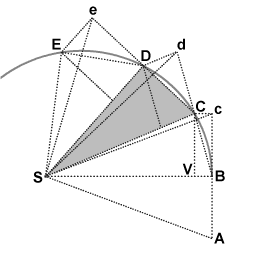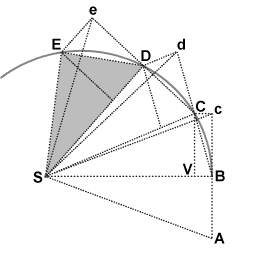
Kepler created the laws of planetary motion, but Newton was the one who used this information to come up with angular momentum. He used a combination of triangles to geometrically prove that the area swept out by an object is equal in all places given that the change in time is the same. The height of these triangles is the tangential velocity and the base of these triangles is the radius of orbit. So, if the area swept out by an object must stay constant with a constant change in time, and velocity or radius changes in magnitude, the other variable must counteract this change! | |||
[[File:File-Newton area law derivation.gif]] | |||
== See also == | == See also == | ||
===Further reading=== | ===Further reading=== | ||
===External links=== | ===External links=== | ||
| Line 66: | Line 118: | ||
==References== | ==References== | ||
Print Sources: | |||
* Chabay, Sherwood. ''Matter and Interactions''. 3rd Ed. Hoboken: Wiley, 2011. | |||
Online Sources: | |||
* http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html | |||
Latest revision as of 23:16, 18 April 2018
Claimed by clindbeck3 (Christopher Lindbeck) for Spring 2018 Is currently a work in progress, in heavy flux April 18th 2018.
I believe there may be a solid argument for moving the contents of this page onto another page as a top level section. When it comes down to it we usually talk about angular momentum in relation to linear momentum anyway so it is difficult for this page to not just redefine angular momentum.
The Main Idea
Linear momentum tends to behave fairly intuitively, but angular momentum has some more obtuse properties that can make it behave in less immediately intuitive ways. While many of the equations describing angular momentum look almost identical to those describing linear momentum, variables that were fixed in linear momentum can change based on multiple factors, this can lead to less intuitive behavior. In addition, angular momentum has two separate components, one of which is relative to a point of reference.
Linear momentum is relatively simple, it depends upon the mass and velocity of an object, and to an extent the equation for angular momentum mimics the equation for linear momentum, but angular momentum draws a relationship between mass, velocity, AND the radius from the axis to the mass about which it is rotating. Now that your motion is relative to an axis, all of a sudden WHERE your mass is in relation to that axis MATTERS, and so the radius wriggles its way into the equations for linear motion, which makes these new equations have similar form but function in a completely different way.
A Mathematical Model
Just like there are simple equations to describe linear momentum there are equally simple equations for describing angular momentum, many of which are extremely similar. What we will come to find however is that some of the variables and factors that we take for granted with linear motion become more complex in angular motion.
For example in a linearly moving system, there is only one type of movement (translational motion), and so it is relatively simple to calculate the momentum of single objects or the momentum of a system which would just be the addition of the momentum for each part.
Linear Momentum vs Angular Momentum Equations
We can see that a number of equations look very similar with variables swapping out for one another one-for-one in equations.
| Linear Motion | Angular (Rotational) Motion |
|---|---|
| Linear Position: [math]\displaystyle{ x }[/math] (m) | Angular Position: [math]\displaystyle{ θ }[/math] (rad) |
| Linear Velocity: [math]\displaystyle{ v }[/math] (m/s) | Angular Velocity: [math]\displaystyle{ ω }[/math] (rad/s) |
| Linear Motion: [math]\displaystyle{ x=\vec{v}t }[/math] | Angular Rotation: [math]\displaystyle{ θ=ωt }[/math] |
| Mass: [math]\displaystyle{ m }[/math] (kg) | Moment of Inertia: [math]\displaystyle{ I }[/math] (kg m^2) |
| Momentum: [math]\displaystyle{ p=m\vec{v} }[/math] | Angular Momentum: [math]\displaystyle{ \vec{L}_{rot}=I\vec{ω} }[/math] |
| Linear Kinetic Energy: [math]\displaystyle{ \frac{1}{2} m v^2 }[/math] | Rotational Kinetic Energy: [math]\displaystyle{ \frac{1}{2} I ω^2 }[/math] |
Keeping in mind that we are primarily looking at rotational angular momentum right now, lets take a look at some of the differences between the two.
ω is fairly similar to linear velocity in most respects. The faster something is spinning the more radians it covers per second and the higher the ω value will be. [math]\displaystyle{ I }[/math] is another matter though, unlike its linear cousin [math]\displaystyle{ m }[/math] it is not a simple unit; Its formula is kg m^2. Moment of Inertia is different from mass in that it depends on weight distribution and axis of rotation, meaning that not only is it different for different in different motions of the same object, it can actually change during motion. These factors are what gives angular momentum its less intuitive properties.
When looking at linear momentum a lot of things are simplified in the fact that mass is constant and easily measurable, but Moment of Inertia is neither of those things and this can mess with our calculations and our mental model of motion. The in-class demonstrations regarding the spinning chair and the rolling cylinders demonstrate this property. Since moment of Inertia can change, objects can change behavior without any external force acting on them by changing shape. The classic example of this is the ice skater tucking in their limbs to achieve high rotational speeds seemingly by magic. They can also seemingly float in the air defying gravity in the case of a gyroscope, or have bizarre behavior without external interaction like the T-handle in space rotating back and forth.
Another major difference between linear and angular momentum is that it has two components, Rotational and Transnational. Transnational angular momentum is different from linear momentum primarily in that it differs based on a point of reference. This can be seen in the fact that it exists as the cross product of two vectors, a position vector relative to a point of reference, and the linear momentum vector.
One of the other elements that we don't typically have to worry about when dealing with linear momentum that comes up in angular momentum is the direction of the momentum vector. With linear momentum it is almost always obvious which direction the momentum is heading, as it is the same direction that the object is heading. With angular momentum we need to use the right hand rule or the cross product to figure out the direction of the momentum vector.
[math]\displaystyle{ L = r x p }[/math]
This cross product is what determines the direction that the angular momentum vector faces, it is also what relates the linear momentum vector to the angular momentum vector. The two vectors form a plane and you know that the angular momentum vector will be orthogonal to that plane due to the nature of the cross product. You can use the right hand rule to figure out which direction that will be in and in many situations will not need to work out the entire cross product.
Like linear momentum angular momentum has a conservation rule. Where linear momentum will not change unless an external force is applied, angular momentum will not change unless an external torque is applied. Torque is essentially the force analog for angular momentum, it causes changes to angular momentum where force causes changes in linear momentum. Torque has the unit N m because that is what it is, a force applied over a radius. Torque is not to be confused with work, for which the formula is also N m.
Direction And the Right Hand Rule
While the direction of linear momentum is rarely difficult to deduce, the direction of angular momentum can often be less intuitive than simply the direction of motion. We use the right hand rule and the cross product with the position vector to figure out what direction our angular momentum vectors should be pointing.
However in a rotational system, we have two different subcategories for angular momentum: translational and rotational. Translational angular momentum depends upon a part's component of momentum that is orthogonal to the radius from a point of reference. Rotational angular momentum depends upon the moment of inertia of each part and how fast it rotates around its own axis, so the point of reference does not play a part in rotational angular momentum (unless the object you are calculating for is coincidentally spinning around that exact point).
- Rotational angular momentum: [math]\displaystyle{ \vec{L}_{rot} = I\vec{ω} }[/math]
- Translational angular momentum: [math]\displaystyle{ \vec{L}_{trans} = |\vec{r}||\vec{p}|sin{θ} }[/math]
- for the direction you can use the right hand rule.
- Total angular momentum: [math]\displaystyle{ \vec{L}_{tot} = \vec{L}_{rot} + \vec{L}_{trans} }[/math]
A Computational Model
Glowscript Link: https://trinket.io/glowscript/239aa4fac7
In this model there is a very simple orbit of a spacecraft around Earth while the Moon also rotates around Earth. Trails have been left out for efficiency. From this model you can observe both linear and angular momentum. When the spacecraft comes near to the Earth, its velocity increases, and you can see this in the vectors represented by arrows. This is because [math]\displaystyle{ \vec{v} = \vec{ω}*r }[/math], therefore [math]\displaystyle{ \vec{ω} }[/math] has increased by this formula. All of the forces on the spacecraft are from within the system and so momentum must be conserved. Now, what is the only way to increase your [math]\displaystyle{ \vec{ω} }[/math] in a system where momentum is conserved and there are no outside forces? Looking at the previous equations, the only way to do this is to decrease [math]\displaystyle{ \vec{I} }[/math]. This can be verified by observing that the spacecraft has indeed moved closer to Earth!
Examples
Simple
Middling
Difficult
Connectedness
- Connection with Mathematics Curriculum
- In multivariable calculus, there is an operation called the cross product, which can be easily derived from the dot product, that can give you some strange things. If you take the magnitude you get the area of a paralellogram, but more relevant to this section if you do not take the magnitude you get a vector orthogonal to the vectors you used in the cross product. There are two vectors that can be orthogonal to two other vectors if those two other vectors span a plane, both have the same magnitude but opposite directions. Which vector you use first in the cross product determines which of these two vectors is your answer, and thus the right hand rule was formed as a shortcut for an easy answer. The operation that you do in determining the cross product actually comes from determinants of matrices from linear algebra which help in determining properties of a matrix or the area of a paralellopipid created by the vectors that make the columns of that matrix. So, this operation was originally utilized for matrices and has now intertwined with physics for angular momentum and torque.
- Interesting Applications
- One of the most interesting things about angular momentum is that you can change [math]\displaystyle{ \vec{I} }[/math] and [math]\displaystyle{ \vec{ω} }[/math] without adding an external force which you cannot do with linear momentum (because [math]\displaystyle{ m }[/math] can never change internally, but [math]\displaystyle{ I }[/math] can). Angular momentum is used heavily in engineering and especially in dynamics. Anytime there are objects interacting with one another in the real world there will be angular momentum involved. If you want to model the motion of an holonomic robotic platform for example, the torque that each wheel exhibits on the chassis as well as the current angular momentum are very important to getting good motion.
- In many applications using angular momentum instead of linear momentum makes more sense and streamlines calculations. Since you can always convert linear momentum into angular momentum by taking the cross product with the position vector you can get rid of all linear momentum vectors and deal exclusively with angular momentum, which may suit systems with lots of rotating components or an central point of reference better than working with linear momentum.
History
Kepler created the laws of planetary motion, but Newton was the one who used this information to come up with angular momentum. He used a combination of triangles to geometrically prove that the area swept out by an object is equal in all places given that the change in time is the same. The height of these triangles is the tangential velocity and the base of these triangles is the radius of orbit. So, if the area swept out by an object must stay constant with a constant change in time, and velocity or radius changes in magnitude, the other variable must counteract this change!
See also
Further reading
External links
- example in space
- example with wheel
- merry go round fun
References
Print Sources:
- Chabay, Sherwood. Matter and Interactions. 3rd Ed. Hoboken: Wiley, 2011.
Online Sources: