Potential Energy of a Pair of Neutral Atoms

by Charlotte Bunch

Potential Energy of a Pair of Neutral Atoms

At first glance it seems silly to think that there would be any kind of interaction between two neutral atoms because they are in fact neutral. This means that there are equal amounts of positive and negative charges in the atom therefore resulting in a zero net charge on each. However, this is not the case due to the way the election cloud around each nucleus behaves at certain distances.

A Mathematical Model

We know that interactions between atoms are similar to the behavior of a spring. And we can approximate the formula for interatomic potential energy as[math]\displaystyle{ U = (1/2)ks^2 - E_M }[/math]

When graphed, this equation gives us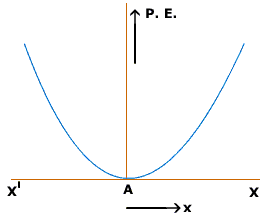

However the potential energy approaches zero as the two atoms get further apart. The Morse approximation accounts for this.

Morse approximation

[math]\displaystyle{ U_M = E_M*[1-e^{-α(r-r_{eq})}]^2 - E_M }[/math]

The new graph looks like this

We can determine a number of properties from this graph. The bottom of the graph represents the point where the potential energy is at a minimum and the change in potential energy with respect to time is 0. This is the distance where no force acts on either of the atoms from the other, and known as the the equilibrium distance, [math]\displaystyle{ r_{eq} }[/math]. If the two atoms are at a distance apart less than [math]\displaystyle{ r_{eq} }[/math] the two will travel in the positive [math]\displaystyle{ r }[/math] direction, or get further apart to reach the minimum potential energy. The opposite is also true. If the two atoms are at a distance apart greater than [math]\displaystyle{ r_{eq} }[/math] the two will travel in the [math]\displaystyle{ -r }[/math] direction, or get closer together.

A Computational Model

This simulations shows the spring like behavior of one neutral atom reacting to another. However, in reality both atoms would be reacting to each other and would stop moving when an equilibrium distance was reached.

Simple Example

There are three cases that describe the potential energy between two neutral atoms.

1. Far apart:
   There is relatively no force on each atom due to the other because the forces of attraction and repulsion of like and unlike charges pretty much cancel out. Because the force between the two atoms dies out at a rate [math]\displaystyle{ 1/r^2 }[/math] the potential energy will also grow closer and closer to zero at large distances.
2. Close together:
   Polarization distorts the electron cloud in such a way that the two atoms feel an attractive force towards each other. Solid objects are held together by this electric force of attraction. When the atoms are close together but at a distance greater than the equilibrium distance, they will be attracted to each other and the slope of the potential energy will be positive.
3. Much closer:
   As the two atoms are pushed closer and closer together they will begin to repel. This is because of the positions of the protons and electrons. When the atoms are at a distance smaller than the equilibrium distance they will repel and the slope of the potential energy graph will be positive.

Noble Gases

The well on the Morse approximation graph is small enough to say that these atoms do not form stable diatomic molecules. Seeing how this graph plots energy vs distance, the depth of the well represents the strength of the diatomic molecule. Because noble gases would have low energy in the diatomic form, a collision between two molecules would likely have enough energy to break the molecules apart.

Connections

1. How is this topic connected to something that you are interested in?
   This topic is connected to something that I am interested in because it amazes me how two atoms that seem should have no attractive or repulsive qualities do. Also, it is interesting to think about how the equilibrium distance is such a delicate balance between attraction and repulsion.
2. How is it connected to your major?
   My major is Nuclear Engineering. This topic is related to my major because it deals with the way atoms interact with each other and that is the basis of what runs a nuclear reactor.
3. Is there an interesting industrial application?
   The industrial application could be anything from creating solids to keeping things in a gaseous state. Finding the equilibrium distance of two atoms can tell you if the atoms will form a better solid, liquid, or gas. And you can use that information to manipulate a solution with those atoms and other elements to either harden or liquify the mixture. You can also develop different processes to make something harden or liquify.

History

Philip Morse

The Morse approximation is accredited to Philip Morse, who wrote a paper in the 1930s about interatomic interactions. He was an engineer and physicists who wanted to get physically applicable results to his findings. Because of this he went on to assist the United States in World War II. He discovered a way to use acoustics to aid the US in detonating German mines. Like many well known physicists, Morse accomplished a great deal because he wanted to use physics to improve the world as it currently was.

See also

Forces that hold atoms and molecules together. HyperPhysics

Further reading

More information on Philip Morse

External links

Internet resources on this topic

References

Matter and Interactions 4th Edition

https://www.aip.org/history/acap/biographies/bio.jsp?morsep

http://www.tutorvista.com/content/physics/physics-iii/work-energy-power/potential-energy-spring.php http://chemwiki.ucdavis.edu/Physical_Chemistry/Quantum_Mechanics/Quantum_States_of_Atoms_and_Molecules/10._Theories_of_Electronic_Molecular_Structure/10.01%3A_The_Born-Oppenheimer_Approximation

http://asa.aip.org/encomia/gold/philipmorse.html