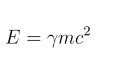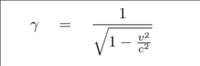Momentum at High Speeds: Difference between revisions
| Line 34: | Line 34: | ||
If you examine the formula for lambda, you will see that as the speed of the object approaches the speed of light, lambda becomes exponentially larger and larger. Thus as you approach light speed, a massive amount of Energy is needed and your momentum is huge. A good computer representation of this is: | If you examine the formula for lambda, you will see that as the speed of the object approaches the speed of light, lambda becomes exponentially larger and larger. Thus as you approach light speed, a massive amount of Energy is needed and your momentum is huge. A good computer representation of this is: | ||
Model: Lambda vs. Speed of Light Graph | |||
[[File:Lambda_vs_Speed_of_Light_Graph.png|200px|thumb alt text]] | |||
==Examples== | ==Examples== | ||
Revision as of 14:49, 3 December 2015
Momentum at High Speeds
By: Dalton Snyder
Short Description of Topic
The Main Idea
State, in your own words, the main idea for this topic Electric Field of Capacitor
A Mathematical Model
Momentum at High Speeds is an adaptation of Einstein's formula for Energy at rest
At Low velocities it is calculated using the formula
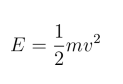
Einstein's Theory of Special Relativity
They found that when you approached the quantum level, the old formula for energy at rest did not apply so it was adapted to quantum mechanics.
This new adapted formula for momentum at high speeds is:
The formula for Lambda is
Lambda Alternate formulas are
A Computational Model
If you examine the formula for lambda, you will see that as the speed of the object approaches the speed of light, lambda becomes exponentially larger and larger. Thus as you approach light speed, a massive amount of Energy is needed and your momentum is huge. A good computer representation of this is:
Model: Lambda vs. Speed of Light Graph
Examples
Be sure to show all steps in your solution and include diagrams whenever possible