Net Force: Difference between revisions
| Line 25: | Line 25: | ||
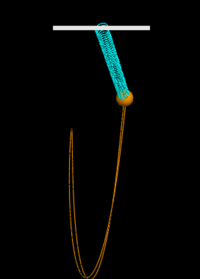
[[File:netforce.png|200px|thumb|left|Tracing the path of a ball/spring model in vpython using net force and the momentum principle.]] | [[File:netforce.png|200px|thumb|left|Tracing the path of a ball/spring model in vpython using net force and the momentum principle.]] | ||
<> | |||
<> | |||
<> | |||
=Simple Example= | =Simple Example= | ||
Revision as of 17:39, 3 December 2015
by Julia Logan
Definition
A Mathematical Model
In order to calculate net force, all EXTERNAL forces acting on a system are added together. The mathematical definition is [math]\displaystyle{ Fnet = F1 + F2 + F3... }[/math]
Additionally, [math]\displaystyle{ Fnet = ma }[/math] where m=mass of the object, and a = acceleration of the object. This is a result of Newton's Second Law of motion. If there is a nonzero net force acting on an object, that object is accelerating (not traveling at a constant velocity). Interestingly, there is zero net force acting on an object if its velocity is constant. This seems counter-intuitive (surely something is causing the object to move!) but makes sense in the context of Newton's Second Law. The forces are balanced (sum to zero) if there is no acceleration, despite any movement that may be happening.
A Computational Model
Net force is an essential component of the Momentum Principle! We can use the Momentum Principle in vpython to update the position of a moving object. But first, we have to find net force.
#1 Fspring = -k*s #2 Fgravmag = mball * g #3 Fgrav = Fgravmag * vector(0,-1,0) #4 Fnet = Fspring+Fgrav #5 pball = pball + Fnet * deltat #6 vball = pball / mball #7 ball.pos=ball.pos+vball*deltat
Here, the spring force and the gravitational force are found using formulas (lines 1-3). Then, they are added together to get the net force on the object (in this case a ball, line 4). The net force is then used in the update form of the momentum principle (line 5). In line 6 the velocity is updated, and line 7 the position is updated. Without net force calculations, tracing an object's path would be impossible.
<> <> <>
Simple Example
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].
Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]
Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.
The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].
The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].
Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page