Net Force: Difference between revisions
| Line 31: | Line 31: | ||
=Simple Example= | =Simple Example= | ||
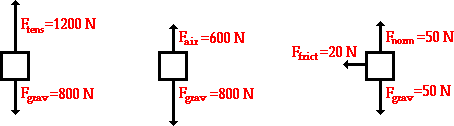
When calculating net force, it is most useful to construct a free body diagram. A free body diagram is a physical representation of the external forces applied to a system. Often, arrows are used to represent forces. In this example, forces are displayed acting on a box. | |||
[[File:forcediagram.gif]] | |||
The first two boxes' net force can be easily calculated by adding the two forces acting on them, respectively. With down being in the negative y direction, for the first box we have:<br> | |||
<math> Fnet = (0, 1200, 0) N + (0, -800, 0) N </math><br> | |||
<math> Fnet = (0, 400, 0) N </math><br> | |||
And the second box:<br> | |||
<math> Fnet = (0, 600, 0) N + (0, -800, 0) N </math><br> | |||
<math> Fnet = (0, -200, 0) N </math><br> | |||
The | The third box has both x-component forces and y-component forces. It is important to separate these in solving for the net force. <br> | ||
y-components:<br> | |||
<math> Fnet,y = (0, 50, 0) N + (0, -50, 0) N </math><br> | |||
<math> Fnet,y = (0, 0, 0) N </math><br> | |||
x-components:<br> | |||
<math> Fnet,x = (-20, 0, 0) N + (0, 0, 0) N </math><br> | |||
Put them together:<br> | |||
<math> Fnet = (-20, 0, 0) N </math><br> | |||
==Connectedness== | ==Connectedness== | ||
| Line 54: | Line 61: | ||
==History== | ==History== | ||
Initially it was believed that force was required to maintain a constant velocity, but this was later cleared up by Sir Isaac Newton's laws of motion and Einstein's theory of relativity in the early 20th century. | |||
== See also == | == See also == | ||
http://www.physicsbook.gatech.edu/Momentum_Principle | |||
http://www.physicsbook.gatech.edu/Conservation_of_Momentum | |||
http://www.physicsbook.gatech.edu/Newton's_Laws_and_Linear_Momentum | |||
===Further reading=== | ===Further reading=== | ||
| Line 70: | Line 79: | ||
==References== | ==References== | ||
http://study.com/academy/lesson/what-is-net-force-definition-magnitude-equations.html | |||
https://en.wikipedia.org/wiki/Net_force | |||
[[Category:Which Category did you place this in?]] | [[Category:Which Category did you place this in?]] | ||
Revision as of 17:06, 3 December 2015
by Julia Logan
Definition
A Mathematical Model
In order to calculate net force, all EXTERNAL forces acting on a system are added together. The mathematical definition is [math]\displaystyle{ Fnet = F1 + F2 + F3... }[/math]
Additionally, [math]\displaystyle{ Fnet = ma }[/math] where m=mass of the object, and a = acceleration of the object. This is a result of Newton's Second Law of motion. If there is a nonzero net force acting on an object, that object is accelerating (not traveling at a constant velocity). Interestingly, there is zero net force acting on an object if its velocity is constant. This seems counter-intuitive (surely something is causing the object to move!) but makes sense in the context of Newton's Second Law. The forces are balanced (sum to zero) if there is no acceleration, despite any movement that may be happening.
A Computational Model
Net force is an essential component of the Momentum Principle! We can use the Momentum Principle in vpython to update the position of a moving object. But first, we have to find net force.
#1 Fspring = -k*s #2 Fgravmag = mball * g #3 Fgrav = Fgravmag * vector(0,-1,0) #4 Fnet = Fspring+Fgrav #5 pball = pball + Fnet * deltat #6 vball = pball / mball #7 ball.pos=ball.pos+vball*deltat
Here, the spring force and the gravitational force are found using formulas (lines 1-3). Then, they are added together to get the net force on the object (in this case a ball, line 4). The net force is then used in the update form of the momentum principle (line 5). In line 6 the velocity is updated, and line 7 the position is updated. Without net force calculations, tracing an object's path would be impossible.
<> <> <>
Simple Example
When calculating net force, it is most useful to construct a free body diagram. A free body diagram is a physical representation of the external forces applied to a system. Often, arrows are used to represent forces. In this example, forces are displayed acting on a box.
The first two boxes' net force can be easily calculated by adding the two forces acting on them, respectively. With down being in the negative y direction, for the first box we have:
[math]\displaystyle{ Fnet = (0, 1200, 0) N + (0, -800, 0) N }[/math]
[math]\displaystyle{ Fnet = (0, 400, 0) N }[/math]
And the second box:
[math]\displaystyle{ Fnet = (0, 600, 0) N + (0, -800, 0) N }[/math]
[math]\displaystyle{ Fnet = (0, -200, 0) N }[/math]
The third box has both x-component forces and y-component forces. It is important to separate these in solving for the net force.
y-components:
[math]\displaystyle{ Fnet,y = (0, 50, 0) N + (0, -50, 0) N }[/math]
[math]\displaystyle{ Fnet,y = (0, 0, 0) N }[/math]
x-components:
[math]\displaystyle{ Fnet,x = (-20, 0, 0) N + (0, 0, 0) N }[/math]
Put them together:
[math]\displaystyle{ Fnet = (-20, 0, 0) N }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Initially it was believed that force was required to maintain a constant velocity, but this was later cleared up by Sir Isaac Newton's laws of motion and Einstein's theory of relativity in the early 20th century.
See also
http://www.physicsbook.gatech.edu/Momentum_Principle http://www.physicsbook.gatech.edu/Conservation_of_Momentum http://www.physicsbook.gatech.edu/Newton's_Laws_and_Linear_Momentum
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
http://study.com/academy/lesson/what-is-net-force-definition-magnitude-equations.html https://en.wikipedia.org/wiki/Net_force