Vectors: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
[[File:Addingvectors.jpg|275px|thumb|center|Adding vector A to B]] | [[File:Addingvectors.jpg|275px|thumb|center|Adding vector A to B]] | ||
<!--{{spaces|2}}--> | |||
To subtract two vectors reverse the direction of the one you want to subtract and continue to add them like shown before. | To subtract two vectors reverse the direction of the one you want to subtract and continue to add them like shown before. | ||
| Line 19: | Line 21: | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
Vectors are given by x, y, and z coordinates. They are written in the form A = <x, y, z> or xi + yj - zk. | |||
Magnitude: : <math> |A| = sqrt{x^2 + y^2 + z^2} </math> | |||
===A Computational Model=== | ===A Computational Model=== | ||
| Line 40: | Line 43: | ||
==History== | ==History== | ||
Giusto Bellavitis abstracted the basic idea of a vector in 1835 when he established the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent. He found a relationship and created the first set of vectors. | |||
The name vector was given to us by William Rowan Hamilton as part of his system of quaternions. The vectors he used were three dimensional. | |||
Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today. He thought of ideas similar to the cross product and vector differentiation. | |||
== See also == | == See also == | ||
Revision as of 02:31, 4 December 2015
Written by Elizabeth Robelo
The Main Idea
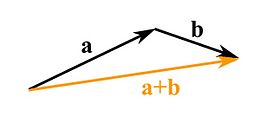
A vector is an object with a magnitude and a direction. It is represented by an arrow. The length of the arrow is the vector’s magnitude and the direction the arrow points is its direction. The start of the arrow is called the tail. The end where the arrow head is located is called the head.
Vectors can be added and subtracted to each other. To add two vectors you put them head to tail. The connecting arrow starting from the tail of one to the head of the other is the new vector.
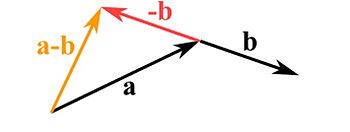
To subtract two vectors reverse the direction of the one you want to subtract and continue to add them like shown before.
A Mathematical Model
Vectors are given by x, y, and z coordinates. They are written in the form A = <x, y, z> or xi + yj - zk. Magnitude: : [math]\displaystyle{ |A| = sqrt{x^2 + y^2 + z^2} }[/math]
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Giusto Bellavitis abstracted the basic idea of a vector in 1835 when he established the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent. He found a relationship and created the first set of vectors.
The name vector was given to us by William Rowan Hamilton as part of his system of quaternions. The vectors he used were three dimensional.
Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today. He thought of ideas similar to the cross product and vector differentiation.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
This section contains the the references you used while writing this page