Pendulum Motion

--mbriatta3 (talk) 14:17, 3 December 2015 (EST)

The pendulum is a mass hanging from a string of negligible mass that is fixed to a point. The equilibrium position of the pendulum is the position when the string and mass hang vertically downward. When pulled back away from this equilibrium state, the string and mass will swing back and forth. If there is no friction or air resistance applied then the pendulum will swing forever.

The Main Idea

Properties of Pendulum Motion

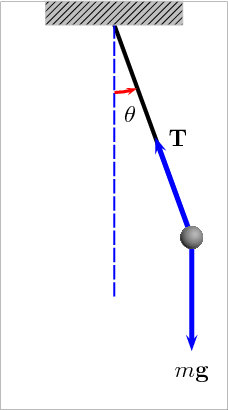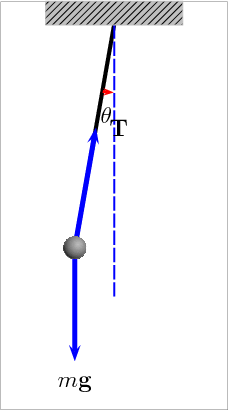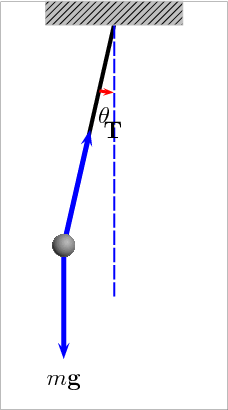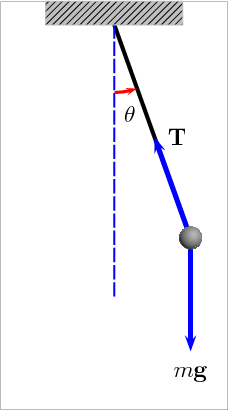
Animation of a pendulum showing forces acting on the mass: the tension T in the rod and the gravitational force mg. Link

A pendulum is just a mass hanging from a spring moving back and forth. In order to describe a pendulum, you need to understand its properties and parameters. There is a string with length L, a mass m hanging from the string, and it is pulled away from its equilibrium, there is an angle measured off the vertical. The two forces acting on the pendulum when it is pulled away from its equilibrium are the string tension, Ft and the gravity, F = mg.

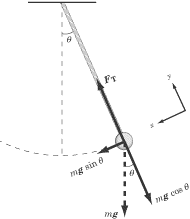
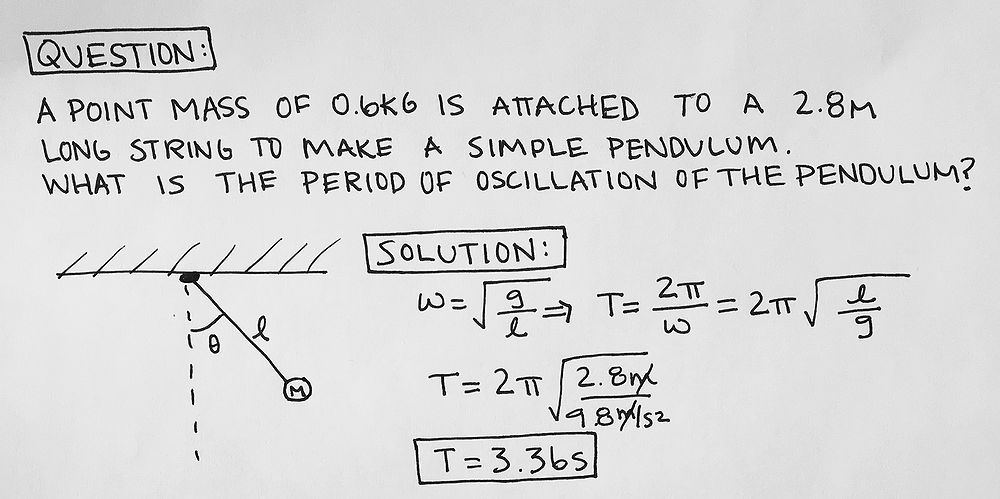
Period of Oscillation

The period of oscillation of the pendulum, T, is defined in terms of the acceleration due to gravity, g, and the length of the pendulum, L, and to a small extent on the maximum angle that the pendulum swings away from vertical, θ₀, called the amplitude

[math]\displaystyle{ T \approx 2\pi \sqrt\frac{L}{g} \qquad \qquad \qquad \theta_0 \ll 1 \, }[/math]

This is a pretty scary-looking equation, but there’s really only one thing you need to gather from it: the longer the pendulum rope, the longer it will take for the pendulum to oscillate back and forth. You should also note that the mass of the pendulum bob and the angle of displacement play no role in determining the period of oscillation.

Energy

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Energy Transformation for a Pendulum

As long as there is no friction applied, mechanical energy in a pendulum is conserved. Total mechanical energy is a combination of gravitational potential energy kinetic energy. As the pendulum swings back and forth, there is a constant exchange between kinetic energy and gravitational potential energy. The potential energy of a pendulum, mgh, increases with the height of the weight as it swings. The image below shows that the potential energy is minimized at the equilibrium and is maximized at θ = ±θ_max The kinetic energy and velocity of the pendulum are maximized at the equilibrium point and minimized when θ = ±θ_max

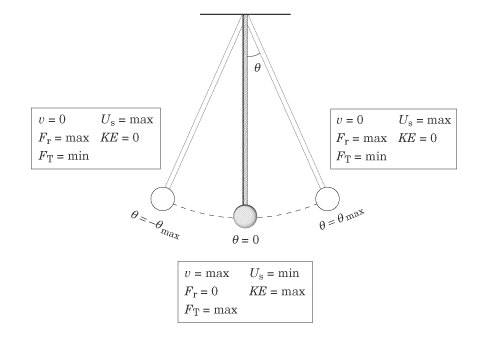
In the figure above, v is velocity, F_r is the restoring force, F_t is the tension in the pendulum string, U_s is potential energy, and KE is kinetic energy.

Velocity

Animation of a pendulum showing the velocity and acceleration vectors. Link

The velocity can be approximated from the gravity equation for a weight dropping from a height.

In order to calculate the the velocity of the pendulum mass at the equilibrium position, you have arrange the coordinate system so that the height of the mass at the equilibrium position is equal to zero. From this we can use the total mechanical energy which is equal to the kinetic energy at the equilibrium point where U = 0. This total mechanical energy also equals the total potential energy at where KE = 0. By putting these equations together we get:

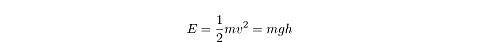
But what is height and how do we find it? The height is determined by the angle from the vertical that is the starting point of the pendulum's swing.

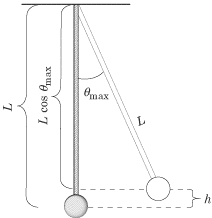
From the figure, we see that If we plug that value into the equation above, we can solve for v: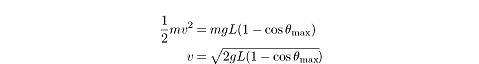

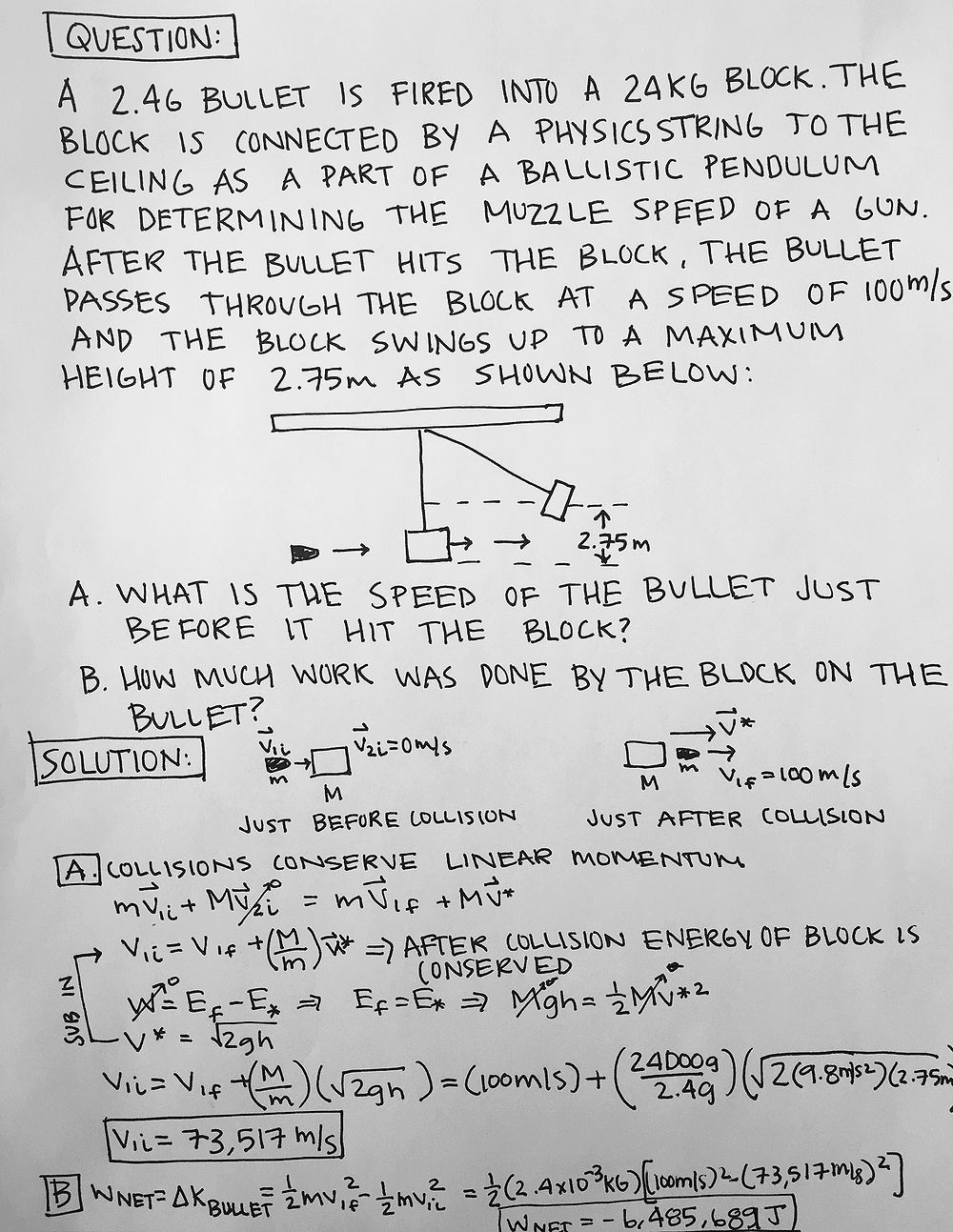
Examples

Simple

Middling

Difficult

Connectedness

In 1656 the Dutch scientist Christiaan Huygens built the first pendulum clock.[34] This was a great improvement over existing mechanical clocks; their best accuracy was increased from around 15 minutes deviation a day to around 15 seconds a day.[35] Pendulums spread over Europe as existing clocks were retrofitted with them.[36]

The English scientist Robert Hooke studied the conical pendulum around 1666, consisting of a pendulum that is free to swing in two dimensions, with the bob rotating in a circle or ellipse.[37] He used the motions of this device as a model to analyze the orbital motions of the planets.[38] Hooke suggested to Isaac Newton in 1679 that the components of orbital motion consisted of inertial motion along a tangent direction plus an attractive motion in the radial direction. This played a part in Newton's formulation of the law of universal gravitation.[39][40] Robert Hooke was also responsible for suggesting as early as 1666 that the pendulum could be used to measure the force of gravity.[37]

During his expedition to Cayenne, French Guiana in 1671, Jean Richer found that a pendulum clock was 2 1⁄2 minutes per day slower at Cayenne than at Paris. From this he deduced that the force of gravity was lower at Cayenne.[41][42] In 1687, Isaac Newton in Principia Mathematica showed that this was because the Earth was not a true sphere but slightly oblate (flattened at the poles) from the effect of centrifugal force due to its rotation, causing gravity to increase with latitude.[43] Portable pendulums began to be taken on voyages to distant lands, as precision gravimeters to measure the acceleration of gravity at different points on Earth, eventually resulting in accurate models of the shape of the Earth.[44]

As you see, the pendulum motion can be seen in our everyday life. As an architecture major, I have always been interested art and design. Different sculptures, installations, and art pieces can even be achieved throughout the application of a pendulum motion. Take a look here and here and here

History

Italian scientist Galileo Galilei was the first to study the properties of pendulums, beginning around 1602.[28] The earliest extant report of his research is contained in a letter to Guido Ubaldo dal Monte, from Padua, dated November 29, 1602.[29] His biographer and student, Vincenzo Viviani, claimed his interest had been sparked around 1582 by the swinging motion of a chandelier in the Pisa cathedral.[30][31] Galileo discovered the crucial property that makes pendulums useful as timekeepers, called isochronism; the period of the pendulum is approximately independent of the amplitude or width of the swing.[32] He also found that the period is independent of the mass of the bob, and proportional to the square root of the length of the pendulum. He first employed freeswinging pendulums in simple timing applications. His physician friend, Santorio Santorii, invented a device which measured a patient's pulse by the length of a pendulum; the pulsilogium.[28] In 1641 Galileo conceived and dictated to his son Vincenzo a design for a pendulum clock;[32] Vincenzo began construction, but had not completed it when he died in 1649.[33] The pendulum was the first harmonic oscillator used by man.[32]

See also

• Barton's Pendulums
• Double Pendulum
• Pendulum Clock
• Pendulum (mathematics)
• Spherical Pendulum
• Simple Harmonic Motion

Further reading

• G. L. Baker and J. A. Blackburn (2009). The Pendulum: A Case Study in Physics (Oxford University Press).
• M. Gitterman (2010). The Chaotic Pendulum (World Scientific).
• Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005)The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives, Springer
• Michael R. Matthews, Colin Gauld and Arthur Stinner (2005) The Pendulum: Its Place in Science, Culture and Pedagogy. Science & Education, 13, 261-277.
• Schlomo Silbermann,(2014) "Pendulum Fundamental; The Path Of Nowhere" (Book)
• Nelson, Robert; M. G. Olsson (February 1986). "The pendulum – Rich physics from a simple system". American Journal of Physics 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. doi:10.1119/1.14703.
• L. P. Pook (2011). Understanding Pendulums: A Brief Introduction (Springer).

External links

[1]

References

• Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
• "Pendulum Motion." Pendulum Motion. Physics Classroom, 1996. Web. 03 Dec. 2015.
• "Pendulum." Wikipedia. Wikimedia Foundation, n.d. Web. 03 Dec. 2015.