Inductance

Made by Mackenzie Rideout

Short Description of Topic

The Main Idea

Inductance is when a current from one coil causes current in a second, coil that is not connected to the original current or coil. A similar affect also happens within singular coils. A coil with current running through it will cause a current in the opposing direction to form. This opposing current actually works to slow down the original current. Because of these opposing currents the original current becomes almost sluggish. This quality is what makes it difficult to increase or decrease any current. Inductance is commonly found in circuits that contain a solenoid.

A Mathematical Model

To be able to successfully compute the inductance of a coil you will have to analyze the magnetic field that surrounds it. In the case of a solenoid, the magnetic field is B=μ0NI/d. For a solenoid this can give you information about the current running through one loop on the solenoid which you can then use to find the current that is running through the entire solenoid from beginning to end. You do this by taking the derivative of the magnetic field with respect to time and then multiplying this result by the number of loops in the solenoid.

A Computational Model

Here is a visual display of inductance in a solenoid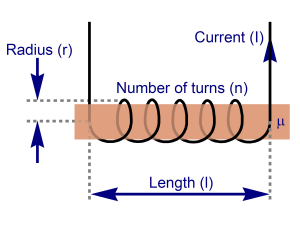

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Emf of an entire solenoid:

B=μ0NI/d emf = |d(mag flux)/dt| = d/dt|μ0NI/d(piR^2)| = μ0NI/d(piR^2)dI/dt emf = N(μ0N/d(piR^2)dI/dt)= (μ0N^2/d(piR^2)dI/dt)

Middling

What is the self inductance of a common solenoid?

-The self inductance is the constant in the inductance formula solved above. This means that the self inductance constant for a solenoid is (μ0N/d(piR^2)

Difficult

What is the self-inductance of a solenoid that has 100 loops, a radius of 5 cm, and is 1 meter long.

- the self inductance would be (μ0100/1(pi.01^2)= 3.95e-8 henries

Connectedness

1. This topic is interesting because solenoids are a very common placed tool. It is important to know how they operate in order to use them to the best of their capabilities.
2. This topic is personally connected to me because of my major. I am a mechanical engineer and am currently enrolled in ME2110, the "robot building class". In this class to assist with our designs, we often used solenoids as deployment mechanism. Being able to learn about this topic while working with the objects hands on in a non-physics environment helped me immensely in my design process and physics career.

History

The history of inductance goes back quite a long time ago and is pretty complicated. In the early 19th century there were actually two scientist discovering inductance in parallel with each other, one in America and one in England. These two scientist names are Joseph Henry and Michael Faraday. Because of this there is no one named founder of inductance, but both of them did receive credit. Inductance now finds itself as one of Faraday's Laws, giving Michael Faraday his due credit. While the units for inductance are "Henries" named after Joseph Henry.

See also

Further reading

Information for this page was found in Matter and Interactions Volume II. If you would like to know more about this topic or other topics like it, please reference this book.

External links

Images were found at http://www.calctool.org/CALC/phys/electromagnetism/solenoid

References

This section contains the the references you used while writing this page