Combining Electric and Magnetic Forces: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 36: | Line 36: | ||
:• To find the magnetic force, you can use the Right Hand Rule as follows (See '''Figure 3''': | :• To find the magnetic force, you can use the Right Hand Rule as follows (See '''Figure 3''': | ||
[[RightHandRule.jpg|thumb| '''Figure 3.''' Magnetic Force Right Hand Rule]] | [[File:RightHandRule.jpg|thumb| '''Figure 3.''' Magnetic Force Right Hand Rule]] | ||
:::1) Thumb in direction of the velocity | :::1) Thumb in direction of the velocity | ||
:::2)Fingers in the direction of the magnetic field | :::2)Fingers in the direction of the magnetic field | ||
Revision as of 12:11, 5 December 2015
Claimed by Alana Kaplan
When a charged particle is moving through a space with present electric and magnetic forces, if the forces are not balanced, the particles trajectory will change. It is important to remember that though the forces, observably, interact with a particle in different patterns, their effects can be quantitatively be compared.
We will first go over the qualitative differences of the two forces:
Electric Forces:
- • A particle being acted upon by an electric force will move in a straight line, in the path, or negative path depending on charge, of the the electric field line (See Figure 1 .
- • Electric fields point in a direction radially outward/ inward of a charged particle. There are four possible scenarios for the interaction of 2 charged particles:
- 1) A (-) charged Particle(1) is acting on a (-) charged particle(2)
- • Particle(2) feels force pointing radially outward from Particle(1)
- 2) A (+) charged Particle(1) is acting on a (-) charged particle(2)
- • Particle(2) feels force pointing radially inward toward Particle(1)
- 3) A (-) charged Particle(1) is acting on a (+) charged particle(2)
- • Particle(2) feels force pointing radially inward toward Particle(1)
- 4) A (+) charged Particle(1) is acting on a (+) charged particle(2)
- • Particle(2) feels force pointing radially outward from Particle(1)
- 1) A (-) charged Particle(1) is acting on a (-) charged particle(2)
Magnetic Forces:
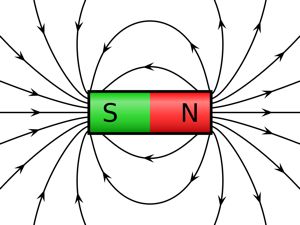
- • The magnetic force on a charged particle is orthogonal to the magnetic field.
- • The particle must be moving with some velocity for a magnetic force to be present.
- • Particles move perpendicular to the magnetic field lines in a helical manner (See Figure 2)
- • To find the magnetic force, you can use the Right Hand Rule as follows (See Figure 3:
- 1) Thumb in direction of the velocity
- 2)Fingers in the direction of the magnetic field
- 3) Your palm will face in the direction of the Magnetic Force
Magnetic and Electric Forces together: