Energy Density: Difference between revisions
Jwilliams436 (talk | contribs) No edit summary |
Jwilliams436 (talk | contribs) No edit summary |
||
| Line 3: | Line 3: | ||
Energy Density is the idea that different objects and fields store varying amounts of energy throughout their area. Energy Density can relate to many different concepts, including fuel sources such as food or oil, however the more physics relevant element of energy density is how it relates to energy stored in Electric and Magnetic fields. | Energy Density is the idea that different objects and fields store varying amounts of energy throughout their area. Energy Density can relate to many different concepts, including fuel sources such as food or oil, however the more physics relevant element of energy density is how it relates to energy stored in Electric and Magnetic fields. | ||
= | =As it Relates to Electric and Magnetic Fields= | ||
== | ==Electric Field== | ||
[[File:CapacitorMoving.png|right|A Moving Capcitor Plate Creating a more energy dense electric field]] | [[File:CapacitorMoving.png|right|A Moving Capcitor Plate Creating a more energy dense electric field]] | ||
| Line 14: | Line 14: | ||
The equation for the Energy Density of an electric field is: | The equation for the Energy Density of an electric field is: | ||
:<math> Energy Density = \frac{\Delta U}{\Delta V} = \frac{\mathbf{E}^2}{2 | :<math> Energy Density = \frac{\Delta U}{\Delta V} = \frac{\mathbf{E}^2 \varepsilon_0}{2} </math> | ||
| Line 21: | Line 21: | ||
As you can infer from the above equation, the Unit for Energy Density of an Electric Field is <math> \frac{J}{m^3} </math>. This comes from the fact that Energy is measured in Joules, and volume is measured in meters cubed. | As you can infer from the above equation, the Unit for Energy Density of an Electric Field is <math> \frac{J}{m^3} </math>. This comes from the fact that Energy is measured in Joules, and volume is measured in meters cubed. | ||
== | ==Magnetic Field== | ||
In a similar manner that Energy can be stored in an electric field, there is also an energy density associated with a magnetic field. Typically, Magnetic Energy density is associated with solenoids and inductance. We won't go through the full derivation, however this concept can be visualized by imagining a circuit that includes an inducting solenoid. Because the circuit has a power going into an inductor, there is work being done. This work is translated into increasing the strong magnetic field inside of the solenoid, essentially converting energy in to a Magnetic field. | |||
== | ===Equation and Units=== | ||
The equation for the Energy Density of a Magnetic Field looks similar to the equation for the Energy Density of an Electric Field. | |||
:<math> Energy Density = \frac{\Delta U}{\Delta V} = \frac{\mathbf{B}^2}{\varmu_0 2} </math> | |||
==Combination of Electric and Magnetic Energy Density== | |||
=Radiation= | |||
=High Energy Density Physics= | |||
Revision as of 15:59, 5 December 2015
by jwilliams436
Energy Density is the idea that different objects and fields store varying amounts of energy throughout their area. Energy Density can relate to many different concepts, including fuel sources such as food or oil, however the more physics relevant element of energy density is how it relates to energy stored in Electric and Magnetic fields.
As it Relates to Electric and Magnetic Fields
Electric Field
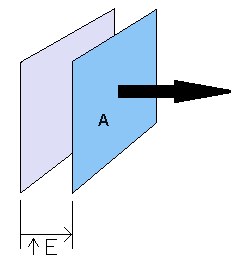
The typical consideration of Energy as it relates to electric fields is the field's interaction with a particle. However, the Energy Density perspective is much more fundamental. It says that energy is physically stored in electric fields. To wrap your head around this idea, imagine a system of two oppositely charged capacitor plates in which you slowly pull one plate away from the other. In this scenario, the space where there is a sizable electric field increased, due to the energy expended by you. In this sense, energy is stored in the electric field.
Equation and Units
The equation for the Energy Density of an electric field is:
- [math]\displaystyle{ Energy Density = \frac{\Delta U}{\Delta V} = \frac{\mathbf{E}^2 \varepsilon_0}{2} }[/math]
Where [math]\displaystyle{ \Delta U }[/math] is the Potential Energy, [math]\displaystyle{ \Delta V }[/math] represents the Volume, [math]\displaystyle{ \mathbf{E} }[/math] is the Electric Field, and [math]\displaystyle{ \varepsilon_0 }[/math] is the vacuum permittivity constant (8.85e-12).
As you can infer from the above equation, the Unit for Energy Density of an Electric Field is [math]\displaystyle{ \frac{J}{m^3} }[/math]. This comes from the fact that Energy is measured in Joules, and volume is measured in meters cubed.
Magnetic Field
In a similar manner that Energy can be stored in an electric field, there is also an energy density associated with a magnetic field. Typically, Magnetic Energy density is associated with solenoids and inductance. We won't go through the full derivation, however this concept can be visualized by imagining a circuit that includes an inducting solenoid. Because the circuit has a power going into an inductor, there is work being done. This work is translated into increasing the strong magnetic field inside of the solenoid, essentially converting energy in to a Magnetic field.
Equation and Units
The equation for the Energy Density of a Magnetic Field looks similar to the equation for the Energy Density of an Electric Field.
- [math]\displaystyle{ Energy Density = \frac{\Delta U}{\Delta V} = \frac{\mathbf{B}^2}{\varmu_0 2} }[/math]
Combination of Electric and Magnetic Energy Density
Radiation
High Energy Density Physics
Sustainable Energy
There is currently a significant Global Discussion relating to the future of our energy sources. At this point, we have identified that fossil fuels such as oil or coal are not only limited, but also have an extreme negative impact on the environment. For this reason, there is an effort to find energy sources that not only are unlimited and renewable, but also provide the same amount of efficiency (Energy per volume or weight) as current fossil fuels. The problem is that fossil fuels far and away have the highest energy density of almost any current energy source. The table below shows a comparison of Energy Densities of several different popular fuel sources.
| Fuel Source | Energy Density (Wh/Kg) | Energy Density (Wh/L) |
|---|---|---|
| Gasoline | 9,000 | 13,500 |
| Propane | 6,600 | 13,900 |
| Ethanol | 6,100 | 7,850 |
| Liquid Hydrogen | 2,600 | 39,000 |
| Lithium Ion Battery | 250 | 350 |
| Liquid Nitrogen | 65 | 55 |
| Compressed Air | 17 | 34 |
As you can see, the three fossil fuels have much higher energy densities than the more sustainable options near the bottom. The only exception here is Pressurized Hydrogen, which is exceedingly explosive and dangerous.
For us to truly solve the issue of non-sustainable fuel, the scientists will need to find ways to increase the energy densities of non-fossil fuels before any widespread adoption of them can take place.
Path Independence
The potential difference between two locations does not depend on the path taken between the locations chosen.
A Mathematical Model
In order to find the potential difference between two locations, we use this formula [math]\displaystyle{ dV = -\left(E_x*dx + E_y*dy + E_z*dz\right) }[/math], where E is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
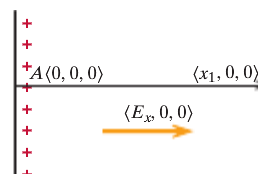
Simple Example
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].
Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]
Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.
The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].
The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].
Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.
As It Relates to Specific Energy
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page