Lorentz Force

Claimed by Firas Sheikh--Fsheikh6 (talk) 21:09, 1 November 2015 (EST)

The Main Idea

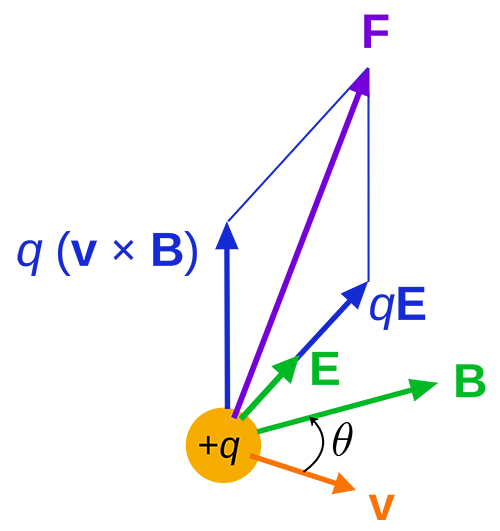
The Electric and Magnetic Forces can be combined into a single force called the "Lorentz Force." This combination of the two forces is useful in applications where a magnetic field and electric field act on a specific particle or series of particles.

A Mathematical Model

[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math] where qE is the electric force and qv x B is the magnetic force.

A Computational Model

The following link provides a good model of the Lorentz Force as well: [[1]]

Examples

Simple

If the Electric Force points in the +x direction and the Magnetic Force points in the –x direction, what direction the Lorentz Force point in? Solution: The Lorentz Force is 0 N.

Middling

The electric force on a certain particle is <500,-200,300> N and the magnetic force is <-200,700,400> N. Find the Lorentz Force. Solution: Lorentz Force = Electric Force + Magnetic Force Lorentz Force = <500,-200,300> + <-200,700,400> = <300,500,700> N

Difficult

The speed of the proton is 5e3 m/s. The magnitude of the Electric Field on the proton is 8e-6 N/C and the magnitude of the magnetic field at that same proton is 4e-9 T. Find the Lorentz Force on this proton. Force Electric = qE = (1.6e-19)*(8e-6) = 1.28e-24 N Force Magnetic = q*B*v = (1.6e-19)*(4e-9)*(5e3) = 3.2e-24 N Force Lorentz = Force Electric + Force Magnetic = 4.48e-24 N

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Early attempts to quantitatively describe the electromagnetic force were made in the mid-18th century. It was proposed that the force on magnetic poles, by Johann Tobias Mayer and others in 1760, and electrically charged objects, by Henry Cavendish in 1762, obeyed an inverse-square law. However, in both cases the experimental proof was neither complete nor conclusive. It was not until 1784 when Charles-Augustin de Coulomb, using a torsion balance, was able to definitively show through experiment that this was true. Soon after the discovery in 1820 by H. C. Ørsted that a magnetic needle is acted on by a voltaic current, André-Marie Ampère that same year was able to devise through experimentation the formula for the angular dependence of the force between two current elements. In all these descriptions, the force was always given in terms of the properties of the objects involved and the distances between them rather than in terms of electric and magnetic fields. The modern concept of electric and magnetic fields first arose in the theories of Michael Faraday, particularly his idea of lines of force, later to be given full mathematical description by Lord Kelvin and James Clerk Maxwell. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, in the time of Maxwell it was not evident how his equations related to the forces on moving charged objects. J. J. Thomson was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode rays, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as F = (q/2)*v X B.

See also

The Hall Effect explores this concept more in depth because it deals with the Electric Force and Magnetic Force being equal. Usually, these problems require you to set them equal to each other and solve for B,v, or E.

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page