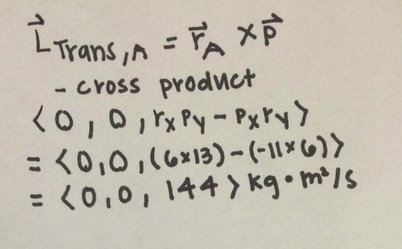Translational Angular Momentum

"Orbital" Angular Momentum Motion

Claimed by: Dhanusha Subramani

The Main Idea

Angular momentum describes the rotational motion of an object; it encompasses the translational and rotational angular momentum. The translational angular momentum deals with motion that can be described as orbital angular motion such as the orbits of the planets around the Sun in a bound system. When compared to the rotational angular momentum, we can see that the translational angular momentum doesn't take into account angular velocity or the inertia of the object(s); it simply deals with the distance(radius) and the momentum.

A Mathematical Model

The magnitude of Translational Angular Momentum is calculated using the magnitudes of the position and momentum vectors and the sin of the angle between the two vectors (θ). This is also technically equal to the cross product of the position and momentum vectors. (The position and momentum of the object are taken at a particular instant, so it is difficult to determine the object's future or past motion or path.)

The direction of the Translational Angular Momentum can be determined using the right-hand rule. The positive z axis (+z) indicates that the object is moving counterclockwise in an xy plane while the negative z axis (-z) indicates that the object is moving counterclockwise.

In order to use the right hand rule, do the following: 1. Curl your fingers in the direction of the object's rotational motion (clockwise or counterclockwise). 2. Stick your thumb out while keeping your hand in the same position. The direction that your thumb is now pointing in is the direction of the angular momentum.

The thumb points out of the plane indicating that the direction is in the +z axis.

The thumb points into the plane indicating that the direction is in the -z axis.

The direction can also be determined using the position and momentum vectors. In order to do this via the right hand rules, point your hand in the direction of the r vector (fingers should be pointing in its direction/path). Next, curl or fold your hand to point through the angle theta, so the palm of your hand should be facing the momentum vector. Stick your thumb out, and this unit vector represents the direction of the angular momentum vector.

The perpendicular component of the r vector represents the product of the position times the sine of the angle. This distance can be determined by drawing a line perpendicular to the momentum vector. The perpendicular distance is then the line that goes from the tail of the r vector to the line that the momentum vector points to.

It is useful to think of the translational angular momentum as relative to a certain location, A, because this will help determine the momentum as specific to the location and instant, making the calculations more accurate and useful for application.

A Computational Model

https://youtu.be/EyHxp10497s

Here is some VPython coding that I screen captured that allows us to visual angular momentum in its two components (translational and rotational). When we run the code in VIDLE, we can see that there are two separate rods: the barbell which consists of the rod and two small masses and another rod which connects to the barbell. Only the barbell exhibits translational angular momentum because of the change in its displacement as it rotates; the barbell has no rotational angular momentum because it doesn't have its own axis about which it rotates (the second rod does have rotational angular momentum however).

Examples

Simple

Here is also a very simple, straightforward example from the book.

This example uses the main magnitude formula for calculating the translational angular momentum. The velocity is calculated by dividing the circumference of the circular orbit by the time (seconds) then is multiplied by the Earth's mad to determine the momentum vector. The magnitudes of the position and momentum vectors are multiplied by the sin of 90 degrees because that's the angle between the position and momentum vectors. Since the angle, and magnitudes of the position and momentum vectors are the same at position A and B, the magnitude of the translational angular momentum remains the same, as well.

Middling

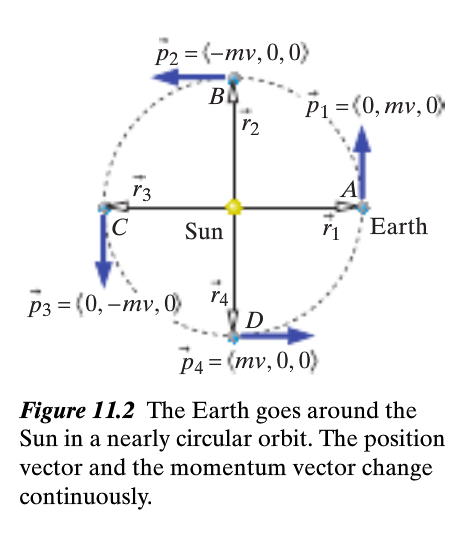
Using the figure below, calculate the z component of the the translational angular momentum for each of the particle as defined by the plane below.

Particles 1,2,3, and 4 all have negative values for the z component via the right hand rule comparing the position and momentum vector directions which shows that the thumb extends into the page (-z direction). Particle 5 has a value of 0 because the r vector magnitude would be 0. Particle 6 has a value of 0 because even though it has a position magnitude, the position vector and momentum vector point in the same direction, meaning that the angle in between the two is 0.

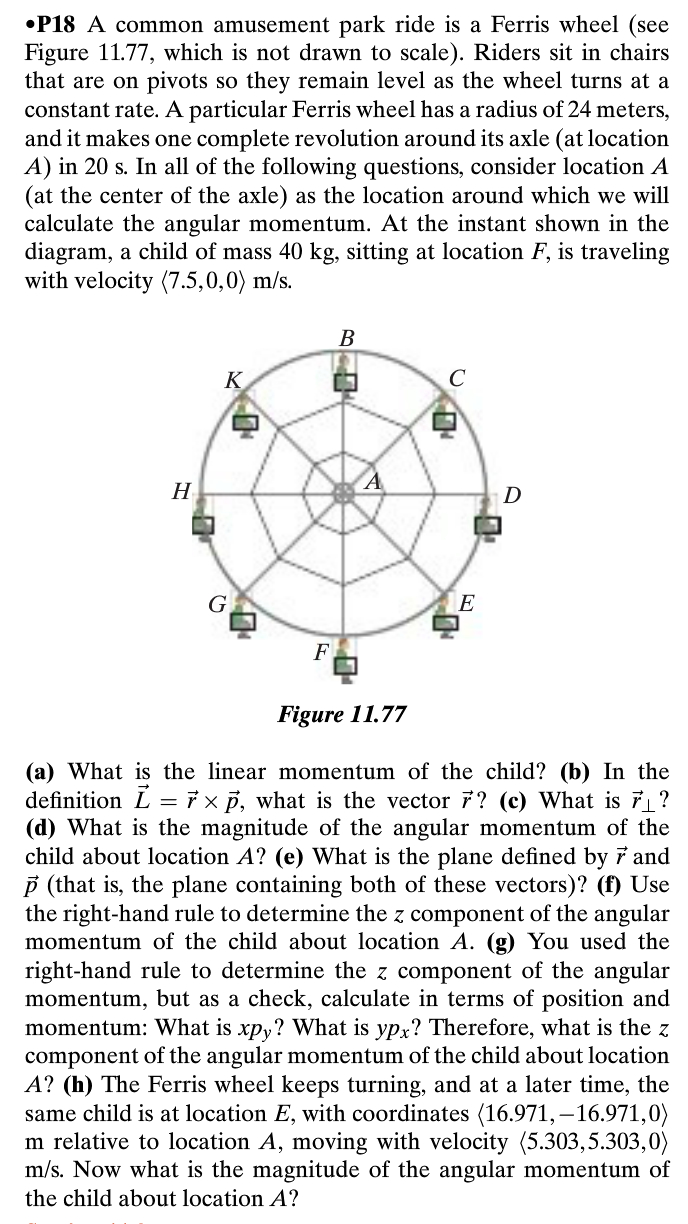
Here is also a similar example from Exam 4 following the same methodology and approach:

Difficult

Solution:

Connectedness

Connected to something I'm interested in: Connected to major: Interesting industrial application:

History

We can contribute the idea of orbits to Kepler. The idea of angular momentum itself, however, is credited to none other than Einstein.

See also

This topic relates to the entirety of the angular momentum section as a whole since it's the basis on which to build upon.

Total Angular Momentum

Further reading

Books, Articles or other print media on this topic

External links

http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/qangm.html

https://en.wikipedia.org/wiki/Angular_momentum

http://www.newworldencyclopedia.org/entry/Angular_momentum

References

Georgia Tech Physics 2211 Exam 4 Fall 2015

Matter and Interactions by Ruth Chabay and Bruce Sherwood (4th Edition)