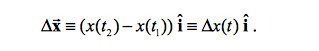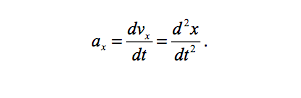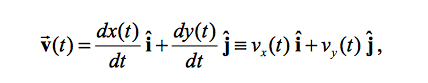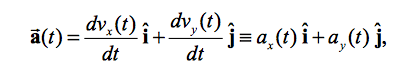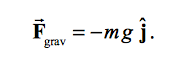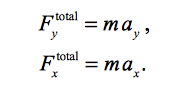Kinematics

Claimed by Nicholas Dillard (ndillard3) Short Description of Topic

The Main Idea

The study of Kinematics is deeply rooted in modeling movement through mathematical equations and analysis. Central to the concept of movement are reference frames and coordinate system. These help answers the question, "what is the object moving relative to, and in what direction?" An example answer may be, "the car is moving relative to the ground, in the direction 20 degrees East of North."

Perhaps the most apparent components of motion are position and time. In laymen's terms, motion is a result of an objects change in position relative to a reference frame over an interval of time. Through this simple relationship, increasingly complex concepts such as velocity, acceleration, kinetic energy, and momentum can be derived. Subsequently, Kinematics lies at the center in the study of physics, and mastery of this area will spill into countless other areas.

A Mathematical Model

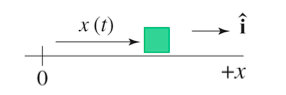
In order to construct a mathematical model of motion, it is important to understand that position can be represented as a vector quantity, having both direction and magnitude. First, let's consider an object moving in one dimension, on per se, the x-axis. The following function (on the left) models the object's position as a function of time, as depicted in the graph pictured to the right.

To construct a function x(t), it is important to understand change in time. Change of time is modeled by the final time observed minus the initial time, as seen in the following equation.

Secondly, we need to determine a functions displacement over a period of time. Displacement is described as an objects change in position, as described in the following equation.

If you divide an object's displacement over a period in time, the result is average velocity, which is also a vector quantity. Instantaneous velocity is a function of time, which models an objects movement relative to a frame of reference, and is the first derivative of displacement with respect to time. Velocity, like most things in life, can change. This is known as acceleration. Imagine a time when when you were riding in a car, and the driver took off from rest. Acceleration is mathematically modeled as an objects change in velocity over a period of time, or in calculus as the first derivative of velocity with respect to time (instantaneous acceleration).

In multi-dimensions, motion can be described in a similar manner, using the unit vectors i, j, and k.

The multi dimensional acceleration vector a is modeled similarly

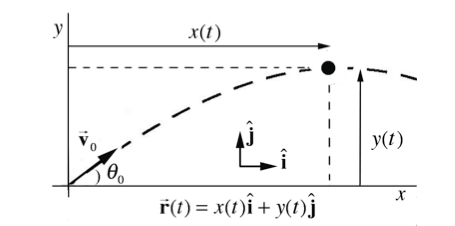
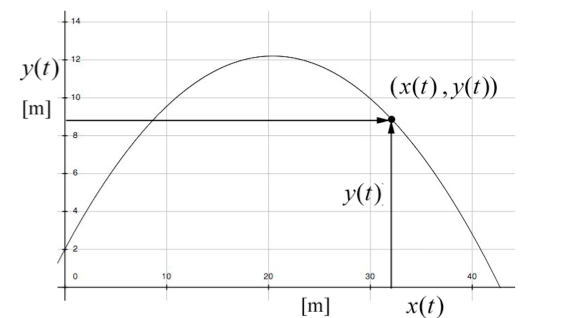
Introductory study of kinematics is often centered around projectile motion problems. Consider the motion of a body that is release at time t = 0 with an initial velocity v at height h above the ground. To analyze problems of this type, choose coordinates with the y-axis in the vertical direction with j pointing upwards and the x-axis in the horizontal direction with i pointing in the direction the object is moving horizontally. Choose the origin to be the point where the object is released. The following figure depicts this coordinate system of the object at time t.

To conclude our study of motion, the fundamental concepts of Force are explored. The only force acting on objects is the gravitation attraction between the object and the earth. The force acts downward with a magnitude of mg, where m is equal to mass, and g is equal to the acceleration of gravity (9.81 m/s^2). Newton's second law states that the net force on an object is a product of the object's mass and its acceleration vector a. The components in the x and y direction can be evaluated individually in this vector equation.

The following equations will be useful in solving problems related to kinematics.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

An airplane accelerates down a runway at 3.20 m/s2 for 32.8 s until is finally lifts off the ground. Determine the distance traveled before takeoff.

Solution: d = 1720 m

Using the following formula

Middling

A person throws a stone at an initial angle θ = 45 from the horizontal with an initial speed of v =20m⋅s-1. The point of release of the stone is at a height d=2m above the ground. You may neglect air resistance. a) How long does it take the stone to reach the highest point of its trajectory? b) What was the maximum vertical displacement of the stone? Ignore air resistance.

Solution: Choose the origin on the ground directly underneath the point where the stone is released. We choose upwards for the positive y-direction and along the projection of the path of the stone along the ground for the positive x-direction. Set t = 0 the instant the stone is released. At t = 0 the initial conditions are then x0 = 0 and y0 = d . The initial x - and y -components of the velocity are given by Eqs. (5.1.5) and (5.1.6). At time t the stone has coordinates (x(t), y(t)) . These coordinate functions are shown in the following image:

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

[1]

References

This section contains the the references you used while writing this page