Static Friction

claimed by: mearathu3 Short Description of Topic

The Main Idea

Friction is the resistance to motion between two objects. It is proportional to the force that pushes the two surfaces together and the roughness of the surface. Static friction is the friction between two objects that are not moving. Static friction between the two objects will increase to oppose motion until it reaches a certain point in which the objects move. This point of motion is defined by the coefficient of static friction which is generally greater than the coefficient of kinetic friction.

A Mathematical Model

Friction is defined by the formula:

[math]\displaystyle{ {F}_{friction} = {μ}{F}_{normal} }[/math]

Where μ is the coefficient of friction between the two objects and F_normal is the normal force between the two surfaces.

Static friction is the maximum force just before the two objects enter into motion and it is related to the coefficient of static friction. It is defined as follows:

[math]\displaystyle{ {F}_{max,f} = {μ}_{static}{F}_{normal} }[/math]

Where μ_static is the coefficient of static friction and F_normal is the normal force between the two surfaces. If the force exerted on the objects exceeds the F_max the objects start to move.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Middling

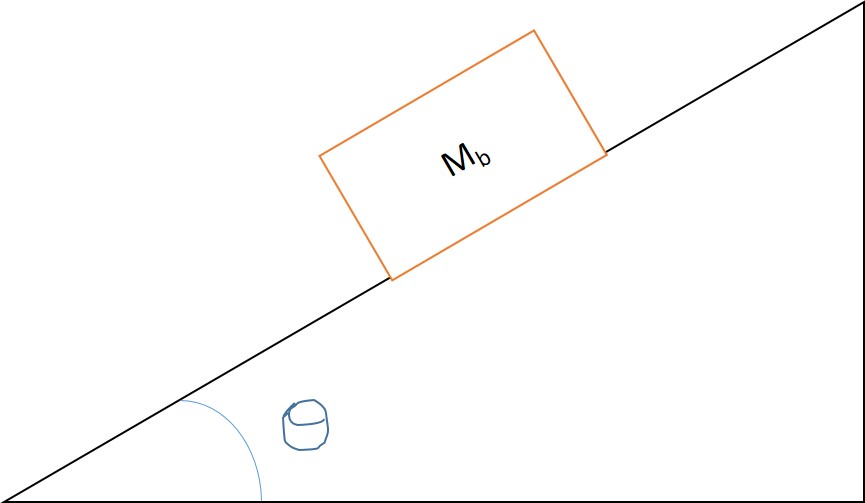
There is a box resting on an incline plane with a mass M_b. The coefficient of static friction between the box and the ramp is μ_s. The box isn’t moving, what is the friction force?

Solution:

To solve the problem the first step required is to identify the free body diagram:

The next step is to calculate the Y component of the F_grav . That will be equal to the F_N .

[math]\displaystyle{ {F}_{N} = {F}_{grav}{sinθ} }[/math]

[math]\displaystyle{ With {F}_{grav} = {9.81}{M}_{b} }[/math]

The final step is to utilize the formula for static friction and the calculated F_N:

[math]\displaystyle{ {F}_{friction} = {F}_{N}{μ}_{s} }[/math]

That solves the problem.

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

[1]

References

The book we used in class was a reference utilized in the creation of this page:

Matter and Interactions 4th edition. Full Citation: Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.