Charged Ring: Difference between revisions
Alicefrancis (talk | contribs) No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
This article will describe the [[Electric Field]] created by a uniformly charged thin ring and how to calculate the value of this field. | This article will describe the [[Electric Field]] created by a uniformly charged thin ring and how to calculate the value of this field. | ||
Redone 10/20/2016 atirumalai3 | |||
==The Main Idea== | ==The Main Idea== | ||
Charges may be arranged in a variety of ways. When points are uniformly distributed a finite distance away from some point, which we define as the origin, we call this curve as a ring. We can position a [[Point Charge]] at every point upon this ring. To analyze this continuous arrangement of charges, we say that their individual contributions are infinitesimally small, and then sum each of these contributions together to arrive at the electric field produced by this charge distribution. To do so, we require the application of an integral. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
This mathematical model is based upon the individual [[Electric Field]] contributions of a number of point charges, each of which are defined by | |||
<math>\vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}</math>. | |||
We also say that this vector field is a member of a linear space of vectors. This is to say that we can apply the [[Superposition Principle]] meaning that we can sum any number of these electric field vectors and obtain another vector which is the electric field vector contributed by those charges. When we continuously sum all of the vectors produced by these charges, we get the electric field produced by the entire arrangement of charges. | |||
===A Computational Model=== | ===A Computational Model=== | ||
| Line 15: | Line 21: | ||
==Step-by-Step Example== | ==Step-by-Step Example== | ||
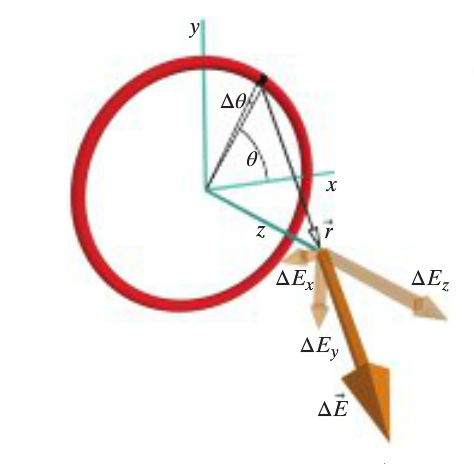
=== | ===Define shape characteristics of the ring=== | ||
The ring has some finite charge. | |||
We see that this arrangement is circular, so a coordinate system with which we can define radial and angular coordinates would be useful. Naturally, this would be the polar coordinate system. | |||
We also see that all charge is uniformly distributed some finite distance R from the center of the ring. It would be useful to let the center of the ring be the origin of our coordinate axes. | |||
Here is a reasonable arrangement for this charged ring. | |||
[[File:Theta.png|options|caption]] | [[File:Theta.png|options|caption]] | ||
=== | Since all charge is concentrated upon the edge of the circle, we can consider our charge distribution to be invariant with respect to radial distance. However, we do see that our charge distribution is function of theta. | ||
===Compute charge distribution function=== | |||
Let us call the charge distribution as <math display="inline">\sigma</math> | |||
We have a charge distributed on the edge of the circle, so | |||
<math> | <math> \sigma=\frac{Q}{2\pi} </math> | ||
<math> \ | |||
<math>\ E=\frac{ | where <math display="inline">Q</math> represents the charge of the ring. | ||
<math>\ E=\frac{Q/ | |||
<math>\ | What this equation means is that the charge is uniformly distributed along each unit of angular length. In this way, it is called angular charge density. | ||
<math>\ E=\frac{ | |||
===Compute infinitesimal charge contribution=== | |||
Let us consider an infinitesimal section of the ring which contains exactly one point charge. The dimension of this section is given by <math display="inline">d\theta</math> which is the infinitesimal angular size. So, the infinitesimal charge contribution, <math display="inline">dQ</math>, is | |||
<math> dQ = \frac{Q}{2\pi}d\theta </math> | |||
===Compute infinitesimal electric field contribution=== | |||
Let us define some arbitrary location at which we are observing this ring of charge. | |||
<math> \vec{r} = x\hat{x}+y\hat{y} + z\hat{z} </math> | |||
in polar coordinates, we see this becomes | |||
<math> \vec{r} = rcos(\theta)\hat{x} + rsin(\theta)\hat{y} + z\hat{z} </math>. | |||
Recall that both sine and cosine are periodic with period of <math>2\pi </math>. This will become important later. | |||
The magnitude of this vector is | |||
<math> \vec{r} = \sqrt{r^{2}+z^{2}} </math> | |||
owing to the usage of the Pythagorean trigonometric identity. | |||
Now, we have what we need to write the electric field vector contributed by each piece of the ring of charge. Let this vector field piece be <math display="inline">d\vec{E}</math>. | |||
<math> d\vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}=\frac{1}{4\pi\epsilon_{0}}\frac{dQ}{(r^{2}+z^{2})^{3/2}}(rcos(\theta)\hat{x}+rsin(\theta)\hat{y}+z\hat{z}) </math> | |||
===Compute electric field vector=== | |||
So, now all that is left is to sum everything up. We are summing over the circumference of a circle, so our path is defined by <math display="inline">0\leq\theta\leq 2\pi </math>. Let us now set up our integral. | |||
<math>\vec{E}=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi(r^{2}+z^{2})^{3/2}}(rcos(\theta)\hat{x}+rsin(\theta)\hat{y}+z\hat{z})d\theta</math> | |||
Since both sine and cosine are <math display="inline">2\pi</math> periodic functions, the <math display="inline">x</math> and <math display="inline">y</math> components of <math display="inline">\vec{E}</math> go to <math display="inline">\vec{0}</math>, which is very convenient. The result is | |||
<math> \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+r^{2})^{3/2}}\hat{z} </math>. | |||
==Connectedness== | ==Connectedness== | ||
The idea of charge density is somewhat analogous to the idea of the mass density, which is useful in a variety of contexts, including the computation of the center of mass, the first and second moments of mass, which are useful in statics and rigid body dynamics. Instead of computing the uniform distribution of the mass of this ring, we are computing the uniform distribution of charge. This concept is also useful in visualizing what happens within a wire in a steady state circuit. The wire can be viewed to be a continuous length of rings of charge, which act as a channel through which electrons are transported, and that the electric field of these rings of charge pushes the electrons within the wire. | |||
It is also important in the context of Maxwell's equations, specifically in Gauss's Law and in the Maxwell-Faraday equation, which are concerned with electron flux and induced fields, respectively. | |||
==History== | ==History== | ||
In 1831, [[Michael Faraday]] showed that when a wire moves within the field of a magnet, it causes an electric current to flow along the wire. Then [[James Maxwell]] published his work, '''Dynamical Theory of the Electric Field''', establishing the connections between electricity and magnetism. | In 1831, [[Michael Faraday]] showed that when a wire moves within the field of a magnet, it causes an electric current to flow along the wire. Then [[James Maxwell]] published his work, '''Dynamical Theory of the Electric Field''', establishing the connections between electricity and magnetism. | ||
== See also == | == See also == | ||
| Line 57: | Line 110: | ||
Nielsen, G. (n.d.). James Clerk Maxwell. Retrieved December 6, 2015, from https://geoffneilsen.wordpress.com/tag/electric-field/ | Nielsen, G. (n.d.). James Clerk Maxwell. Retrieved December 6, 2015, from https://geoffneilsen.wordpress.com/tag/electric-field/ | ||
[[Category:Electric Fields]] | [[Category:Electric Fields]] | ||
Revision as of 20:40, 20 October 2016
This article will describe the Electric Field created by a uniformly charged thin ring and how to calculate the value of this field.
Redone 10/20/2016 atirumalai3
The Main Idea
Charges may be arranged in a variety of ways. When points are uniformly distributed a finite distance away from some point, which we define as the origin, we call this curve as a ring. We can position a Point Charge at every point upon this ring. To analyze this continuous arrangement of charges, we say that their individual contributions are infinitesimally small, and then sum each of these contributions together to arrive at the electric field produced by this charge distribution. To do so, we require the application of an integral.
A Mathematical Model
This mathematical model is based upon the individual Electric Field contributions of a number of point charges, each of which are defined by
[math]\displaystyle{ \vec{E} = \frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} }[/math].
We also say that this vector field is a member of a linear space of vectors. This is to say that we can apply the Superposition Principle meaning that we can sum any number of these electric field vectors and obtain another vector which is the electric field vector contributed by those charges. When we continuously sum all of the vectors produced by these charges, we get the electric field produced by the entire arrangement of charges.
A Computational Model
This VPython code is a representation of adding up the electric fields created by individual pieces of a ring to figure out its electric field.
Step-by-Step Example
Define shape characteristics of the ring
The ring has some finite charge.
We see that this arrangement is circular, so a coordinate system with which we can define radial and angular coordinates would be useful. Naturally, this would be the polar coordinate system.
We also see that all charge is uniformly distributed some finite distance R from the center of the ring. It would be useful to let the center of the ring be the origin of our coordinate axes.
Here is a reasonable arrangement for this charged ring.
Since all charge is concentrated upon the edge of the circle, we can consider our charge distribution to be invariant with respect to radial distance. However, we do see that our charge distribution is function of theta.
Compute charge distribution function
Let us call the charge distribution as [math]\displaystyle{ \sigma }[/math]
We have a charge distributed on the edge of the circle, so
[math]\displaystyle{ \sigma=\frac{Q}{2\pi} }[/math]
where [math]\displaystyle{ Q }[/math] represents the charge of the ring.
What this equation means is that the charge is uniformly distributed along each unit of angular length. In this way, it is called angular charge density.
Compute infinitesimal charge contribution
Let us consider an infinitesimal section of the ring which contains exactly one point charge. The dimension of this section is given by [math]\displaystyle{ d\theta }[/math] which is the infinitesimal angular size. So, the infinitesimal charge contribution, [math]\displaystyle{ dQ }[/math], is
[math]\displaystyle{ dQ = \frac{Q}{2\pi}d\theta }[/math]
Compute infinitesimal electric field contribution
Let us define some arbitrary location at which we are observing this ring of charge.
[math]\displaystyle{ \vec{r} = x\hat{x}+y\hat{y} + z\hat{z} }[/math]
in polar coordinates, we see this becomes
[math]\displaystyle{ \vec{r} = rcos(\theta)\hat{x} + rsin(\theta)\hat{y} + z\hat{z} }[/math].
Recall that both sine and cosine are periodic with period of [math]\displaystyle{ 2\pi }[/math]. This will become important later.
The magnitude of this vector is
[math]\displaystyle{ \vec{r} = \sqrt{r^{2}+z^{2}} }[/math]
owing to the usage of the Pythagorean trigonometric identity.
Now, we have what we need to write the electric field vector contributed by each piece of the ring of charge. Let this vector field piece be [math]\displaystyle{ d\vec{E} }[/math].
[math]\displaystyle{ d\vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r}=\frac{1}{4\pi\epsilon_{0}}\frac{dQ}{(r^{2}+z^{2})^{3/2}}(rcos(\theta)\hat{x}+rsin(\theta)\hat{y}+z\hat{z}) }[/math]
Compute electric field vector
So, now all that is left is to sum everything up. We are summing over the circumference of a circle, so our path is defined by [math]\displaystyle{ 0\leq\theta\leq 2\pi }[/math]. Let us now set up our integral.
[math]\displaystyle{ \vec{E}=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{q}{|\vec{r}|^{2}}\hat{r} d\theta=\int_{0}^{2\pi}\frac{1}{4\pi\epsilon_{0}}\frac{Q}{2\pi(r^{2}+z^{2})^{3/2}}(rcos(\theta)\hat{x}+rsin(\theta)\hat{y}+z\hat{z})d\theta }[/math]
Since both sine and cosine are [math]\displaystyle{ 2\pi }[/math] periodic functions, the [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] components of [math]\displaystyle{ \vec{E} }[/math] go to [math]\displaystyle{ \vec{0} }[/math], which is very convenient. The result is
[math]\displaystyle{ \vec{E}=\frac{1}{4\pi\epsilon_{0}}\frac{Qz}{(z^{2}+r^{2})^{3/2}}\hat{z} }[/math].
Connectedness
The idea of charge density is somewhat analogous to the idea of the mass density, which is useful in a variety of contexts, including the computation of the center of mass, the first and second moments of mass, which are useful in statics and rigid body dynamics. Instead of computing the uniform distribution of the mass of this ring, we are computing the uniform distribution of charge. This concept is also useful in visualizing what happens within a wire in a steady state circuit. The wire can be viewed to be a continuous length of rings of charge, which act as a channel through which electrons are transported, and that the electric field of these rings of charge pushes the electrons within the wire.
It is also important in the context of Maxwell's equations, specifically in Gauss's Law and in the Maxwell-Faraday equation, which are concerned with electron flux and induced fields, respectively.
History
In 1831, Michael Faraday showed that when a wire moves within the field of a magnet, it causes an electric current to flow along the wire. Then James Maxwell published his work, Dynamical Theory of the Electric Field, establishing the connections between electricity and magnetism.
See also
The section on Category:Fields will give some insight into how rings behave in comparison to distributions of charge that form other shapes, and the section entitled Category:Simple Circuits will show you how this charged ring calculation can be used in circuits and real-world applications.
External Links/References
"Electric Field on the Axis of a Ring of Charge". University of Delaware Physics Library. Adapted from Stephen Kevan's lecture on Electric Fields and Charge Distribution. April 8, 1996. http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html
Chabay, R., & Sherwood, B. (2015). Matter and Interactions (4th ed., Vol. 2, pp. 597-599). Wiley.
Energy Access Database. (n.d.). Retrieved December 6, 2015, from http://www.worldenergyoutlook.org/resources/energydevelopment/energyaccessdatabase/
Nielsen, G. (n.d.). James Clerk Maxwell. Retrieved December 6, 2015, from https://geoffneilsen.wordpress.com/tag/electric-field/