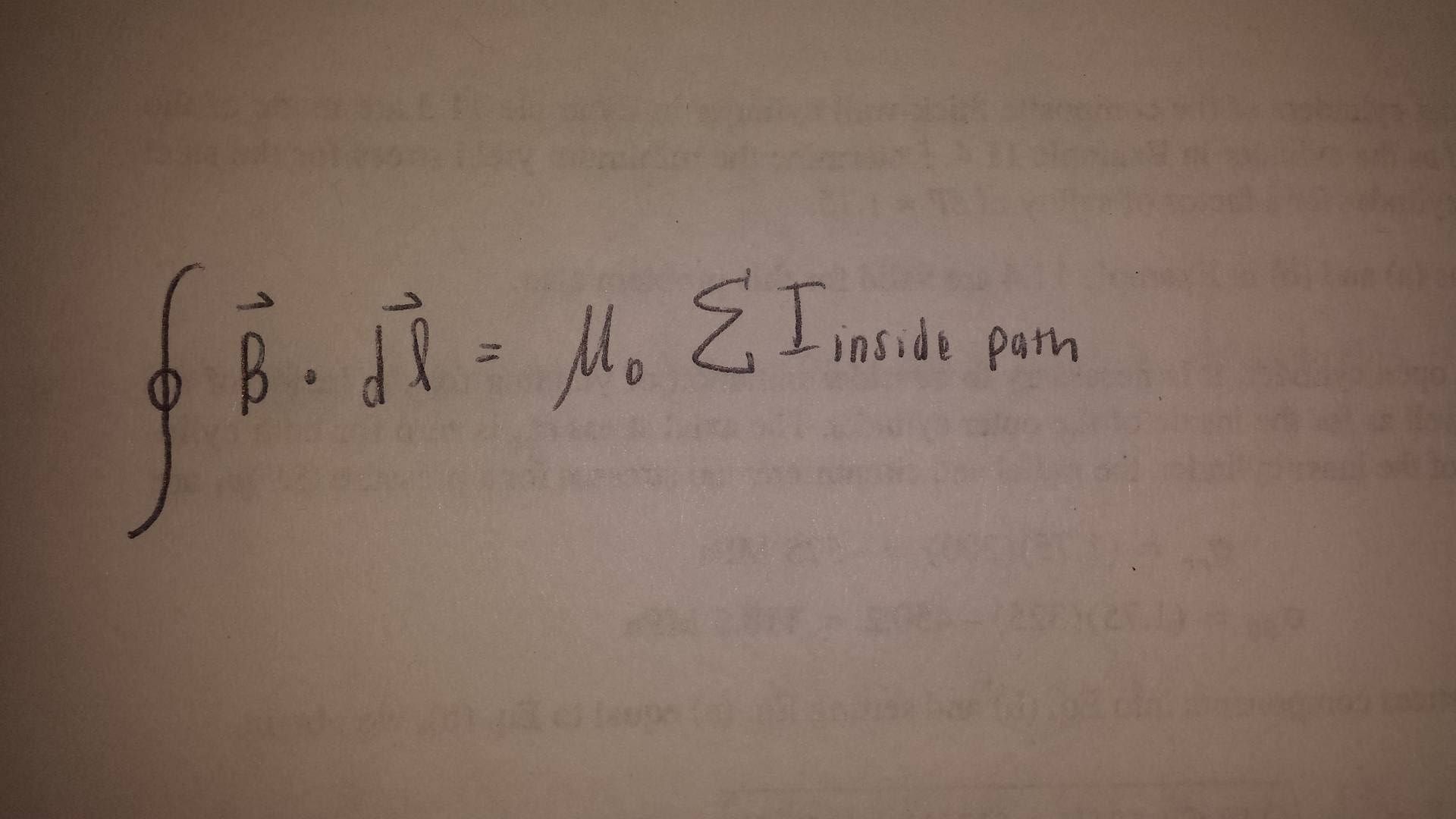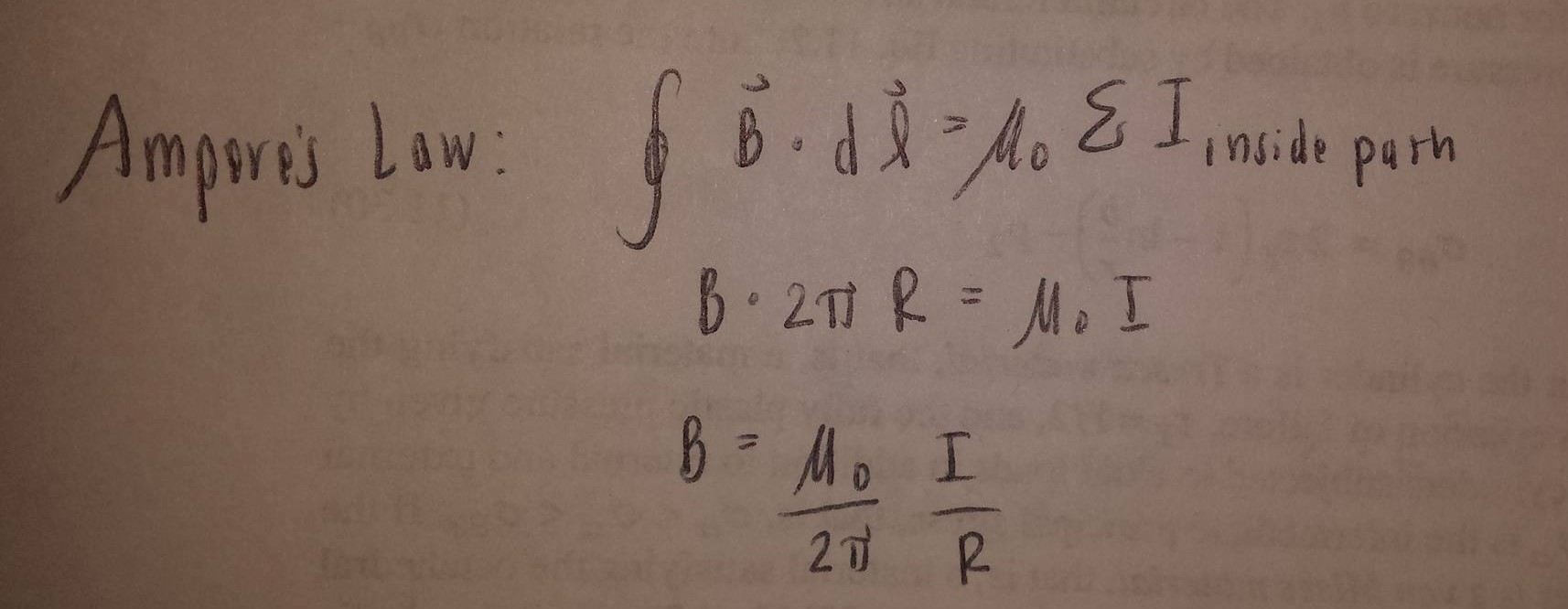Magnetic Field of Coaxial Cable Using Ampere's Law: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
claimed by Parastoo Baradaran-Mashinchi | claimed by Parastoo Baradaran-Mashinchi | ||
Magnetic Field of Coaxial Cable Using Ampere's Law | |||
== Magnetic Field of Coaxial Cable Using Ampere's Law == | |||
| Line 11: | Line 12: | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
Ampere's Law | |||
== Ampere's Law == | |||
[[File:amp1.jpg]] | |||
| Line 41: | Line 46: | ||
==History== | ==History== | ||
Oliver Heaviside designed the [https://en.wikipedia.org/wiki/Coaxial_cable#cite_note-1 Coaxial Cable] in 1880. | |||
== See also == | == See also == | ||
Page for Ampere's Law: [[Ampere's Law]] | |||
More applications: [[Magnetic Field of a Toroid Using Ampere's Law]] and [[Magnetic Field of a Long Thick Wire Using Ampere's Law]] | |||
===External links=== | ===External links=== | ||
| Line 53: | Line 59: | ||
==References== | ==References== | ||
Matter and Interactions | Chabay, Sherwood. (2011). Matter and Interactions (3rd ed.). Raleigh, North Carolina: Wiley. | ||
Exam 4 Fall 2015 Question 3 | Exam 4 Fall 2015 Question 3 | ||
[[Category: | [[Category:Maxwell's Equations]] | ||
Revision as of 00:09, 6 December 2015
claimed by Parastoo Baradaran-Mashinchi
Magnetic Field of Coaxial Cable Using Ampere's Law
The Main Idea
A coaxial cable consists of two cylindrical channels, which is how it derives its name. One of the cylinders carries the current in one direction, surround by an insulating region, and a second cylinder carries the current in the opposite direction, and they are both concentric along the same axis. Coaxial cables are common household items used in many electronics because of their ability to avoid external interference from other fields and for their ability to carry currents for long distances and to be able to exclusively carry their signal in the region between the two conductors. The magnetic field of a coaxial cable can easily be found with the application of Ampere's Law.
A Mathematical Model
Ampere's Law
Examples
A coaxial cable with an outer cylinder of radius R2 surround an inner cylinder of radius R1. They both carry a constant current I, however, in opposite directions. The inner cylinder carries the current to the left and the outer cylinder carries the current to the right. Find the magnitude and direction of the magnetic field when R1< r <R2, or in other words at a distance in between the two cylinders.
We simple have to apply Ampere's Law to the problem and imagine an Amperian surface with a radius of r:
The direction would be clockwise due to the right hand rule. Simply point your thumb in the direction of the current and curl your fingers in the direction of the magnetic field.
What would the magnetic field be at a distance outside of the outer cylinder?
The magnetic field would be zero. This is what is special about coaxial cables-because the current runs in opposing directions, it cancels out at regions outside of the outer cylinder. However, this is only true because the currents are EQUAL and OPPOSITE. If the outer current was greater, the magnetic field would be equal to:
in the opposite direction (counterclockwise).
Connectedness
This technique is applied in everyday life. Coaxial cables are a common household item and are used in many computer and television systems.
History
Oliver Heaviside designed the Coaxial Cable in 1880.
See also
Page for Ampere's Law: Ampere's Law
More applications: Magnetic Field of a Toroid Using Ampere's Law and Magnetic Field of a Long Thick Wire Using Ampere's Law
External links
https://www.youtube.com/watch?v=IMoN6MVgOgA
References
Chabay, Sherwood. (2011). Matter and Interactions (3rd ed.). Raleigh, North Carolina: Wiley.
Exam 4 Fall 2015 Question 3