Magnetic Force in a Moving Reference Frame: Difference between revisions

From Physics Book
Jump to navigation Jump to search
No edit summary
No edit summary
Line 12: Line 12:
First:
First:
Electric force is easily calculated by calculating the electric field, <math>{\vec{E}_{top}}</math>, at the location of proton<math>_{bottom}</math>. The equation for electric force is
Electric force is easily calculated by calculating the electric field, <math>{\vec{E}_{top}}</math>, at the location of proton<math>_{bottom}</math>. The equation for electric force is
<math>{\vec{F}_{E,bottom}} = q_{bottom}{\vec{E}_{top}</math>.
<math>{\vec{F}_{E, bottom}} = q_{bottom}{\vec{E}_{top}}</math>.
Therefore:
<math>{\vec{F}_{E, bottom}} = {\frac{1}{4πϵ_0}}{\frac{e^{2}}{r^{2}}}</math>.


 
Second:
 
Determine magnetic force. <math>{\vec{F}_{M, bottom}}</math> by calculating the magnetic field <math>{\vec{B}_{top}}</math>.
What are the mathematical equations that allow us to model this topic. For example <math>{\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}</math> where '''p''' is the momentum of the system and '''F''' is the net force from the surroundings.
<math>{\vec{B}_{top}} = {\frac{\mu}{4\pi}}</math>


===A Computational Model===
===A Computational Model===

Revision as of 15:36, 6 December 2015

The Main Idea

The magnetic force of a moving charge depends on the velocity of the charge, and thus can differ according to different moving reference frames.

A Mathematical Model

Let's consider two moving protons to simplify the case. Suppose the two protons are initially traveling parallel to each other with the the same speed. The speed is v, and the two particles are distance, r, apart.

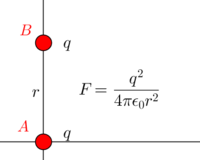
Two protons, distance r apart, moving parallel with velocity, v

How would we find the electric and magnetic force that the top proton exerts on the bottom?

First: Electric force is easily calculated by calculating the electric field, [math]\displaystyle{ {\vec{E}_{top}} }[/math], at the location of proton[math]\displaystyle{ _{bottom} }[/math]. The equation for electric force is [math]\displaystyle{ {\vec{F}_{E, bottom}} = q_{bottom}{\vec{E}_{top}} }[/math]. Therefore: [math]\displaystyle{ {\vec{F}_{E, bottom}} = {\frac{1}{4πϵ_0}}{\frac{e^{2}}{r^{2}}} }[/math].

Second: Determine magnetic force. [math]\displaystyle{ {\vec{F}_{M, bottom}} }[/math] by calculating the magnetic field [math]\displaystyle{ {\vec{B}_{top}} }[/math]. [math]\displaystyle{ {\vec{B}_{top}} = {\frac{\mu}{4\pi}} }[/math]

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Middling

Difficult

Connectedness

  1. How is this topic connected to something that you are interested in?

This topic is interesting because it can be confusing exactly what causes a magnetic force when both the object in question and the reference frame is in motion. The changes in magnetic and electric field due to a change in the reference frame is interesting to note.

  1. How is it connected to your major?

As a BME it is important to be able to understand the consequences or benefits of looking at a phenomenon in a different angle. However, it is important to note that there is only one force resulting from the magnetic and electric fields. Additionally, magnetic forces would be beneficial when dealing with development of devices including current-carrying wires.

  1. Is there an interesting industrial application?

Magnetic forces on current-carrying wires are usually larger than the electric force on the same wire, because the net charge is zero. Moreover, when the speed of the particle is less than the speed of light there is less magnetic interaction between 2 charged particles. When the speed exceeds the speed of light, magnetic force between two charged particles can be compared to the electric force.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Further reading

American Physical Society [1]

External links

Michigan State University: Moving Reference Frames[2]

University of Melbourne: Why do Magnetic Forces Depend on Who Measures Them?[3]

References

http://dx.doi.org/10.1103/PhysRevLett.111.160404

https://www.pa.msu.edu/courses/2000fall/PHY232/lectures/magforces/frames.html

http://www.ph.unimelb.edu.au/~dnj/teaching/160mag/160mag.htm

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Magnetic_Force_in_a_Moving_Reference_Frame&oldid=20164"