Elastic Collisions

CLAIMED BY SEAN FISCHER

The Main Idea

So what exactly is an elastic collision? I know you’re thinking, “Oh I know all about elasticity,” but LOL this is not bubble gum or rubber bands guys!

An elastic collision is a collision between two or more objects in which there is no loss in kinetic energy before and after the collision. If we assume that the colliding objects are part of the system and that there is no force from the surroundings, the final kinetic energy is still in the same form as it was initially. To keep it simple, this means that kinetic energy in= kinetic energy out. Remember how your parents always told you what goes in must come out? They were talking about elastic collisions... probably.

Additionally, elastic collisions are a wonderful representation of the conservation of momentum which states that the momentum of an isolated system is constant. For an isolated system undergoing an elastic collision momentum in = momentum out.

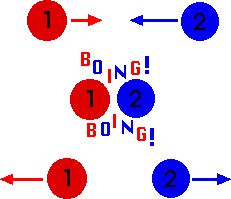
And I love playing pool because every time a ball hits another and they bounce off one another I’m witnessing an elastic collision so basically I’m a physicist in the lab. The image below demonstrates the main idea of an elastic collision. Boing!!

It's important to note that with macroscopic systems there are no perfectly elastic collisions because there's always at least a dab of dissipation (like some thermal energy given off), but most are nearly elastic. The only time there are perfect collisions is on a microscopic level when atomic systems with quantized energy collide, but that's only if there is enough energy available to raise the systems to an excited quantum state-- but quantum energy is really a whole other topic. Let's focus on elastic collisions!

Check out this funny video on elastic collisions also! https://www.youtube.com/watch?v=W9EqU1_DXUw

Now check out this more informative video on elastic collisions: https://www.youtube.com/watch?v=V4vzNk4qppw

A Mathematical Model

Now lets take what we know about elastic collisions and talk about it in mathematical terms. There are three main mathematical concepts surrounding elastic collisions:

---

---

This simple principal can be expanded into:

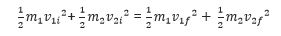
Starting from the left side we have m1 and m2 which are the masses of object 1 and 2 respectively, and v1i and v2i represent their initial velocities respectively. On the right side of the equation, the final kinetic energy, it’s the same equation just different numbers! For the final kinetic energy, unless stuff is breaking or its otherwise stated in the problem, you can assume the masses won’t change BUT the velocities may. Imagine if you toss a pool ball towards another one that is initially at rest. The one that is at rest will move after it is hit, so there is a change in velocity! However, please remember that there is no overall change in kinetic energy. Let’s say the mass of our pool balls are 2 kilograms and I will make up some speeds. Applying the formula from above we get:

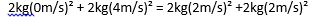
As you see the final velocities changed. One ball was initially at rest but it wasn't after the collision because it was struck by a ball that was already moving...But there was no change in kinetic energy because 32=32 yay! Put it in your calculator and see for yourself.

A Computational Model

The link below demonstrates a basic car crash elastic collision using MATLAB. Take note of the changes in displacement and the time.

Elastic Collision MATLAB model

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Okay let’s start with a simple example like the ones you don't see on the test.

Jay and Sarah are best friends. Since they’re best friends they both weigh 55 kg. Jay hadn’t seen Sarah in a long time so when she saw her she ran to her with a velocity of <4,0,0> m/s. Instead of a hug, they were both too excited and collided and bounced back off of each other, and Sarah flew back with a velocity of <7,0,0> m/s. What was Jay’s final velocity?

Okay, so first let’s think about what we know. This is an elastic collision, so as we mentioned before: Pf = Pi. Breaking that down, we have:

m1v1 + m2v2 = m1v1f + m2v2f, and we are looking for v1f. So let’s rearrange the equation:

v1f= (m1v1 + m2v2) – (m2v2f) / m1

Now, let’s plug in the numbers!

V1f= (55*<4,0,0> + 55*<0,0,0>) – (55*<7,0,0>)/(55)

V1f= <-3,0,0> m/s (Don't forget it's negative because Jay is going in the opposite direction that she started out,not because she's incredibly slow.)

Middling

When far apart, the momentum of a proton is <5.2 ✕ 10−21, 0, 0> kg · m/s as it approaches another proton that is initially at rest. The two protons repel each other electrically, but they are not close enough to touch. When they are far apart again later, one of the protons now has a velocity of <1.75, .82, 0> m/s. At that instant, what is the momentum of the other proton? HINT: Mass of proton is 1.7 *10^-27 kg.

Alright, don't freak out because this collision is on an atomic level, the idea is still the same!

Lets start out with that principle we mentioned before:

Pf= Pi

If we were given the momentum of both protons, we could both subtract one from the other but we only have one velocity and one momentum... but don't forget the hint! We can calculate that second momentum, let's do that first.

mass of proton*velocity=

1.7e-21 * <1.75, .82, 0> = <2.975e-21, 1.394e-21,0> kg * m/s

Okay so now that we have both momentums, we can just subtract the final from the initial right? Right!

<2.975e-21,1.394e-21,0> - <5.2e-21, 0, 0> = <-2.225e-21, -1.394e-21, 0> kg * m/s

There we go!

Difficult

Okay, let's get a little bit trickier here...

There is a 35 kg train travelling at 55 m/s that collides, elastically of course, with a random 2 kg trashcan that's stationary on the tracks. So afterwards, what are the speeds of both the train and the trashcan after the collision?

Let's start out with our handy-dandy momentum in = momentum our principle!

Pf= Pi

m1v1 + m2v2 = m1v1f + m2v2f

Wait, we have two unknowns! So let's plug in numbers:

35*55 + 2*0 = 35*v1f + 2*v2f

1925 = 35*v1f + 2*v2f

Let's multiply this equation by a random number

Let's use the kinetic energy principle now!

1/2mv1^2 = 1/2mv1f^2 + 1/2mv2f^2

Connectedness

So how are collisions connected to the real world? Collisions are all around us!

One main example is cars! Lots of car companies will purposely test and wreck cars to test collisions! Data is then sent to places like the Insurance Institute for Highway Safety where we can learn about car agility and more.

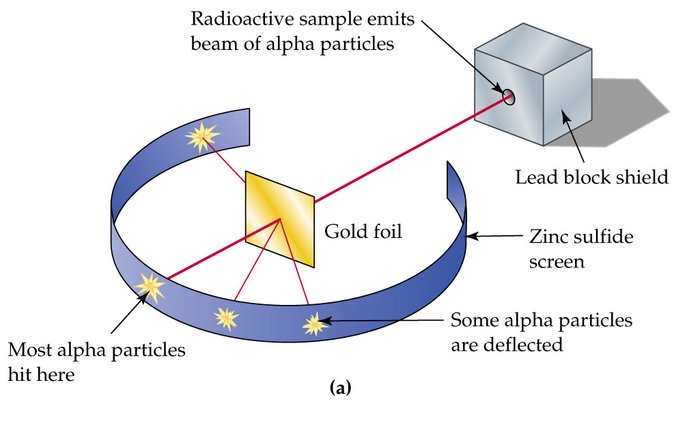
History

The history of collisions originates from the Rutherford Scattering experiment. As Rutherford studied the scattering of alpha particles through metal foils, he first noticed a collision with a single massive positive particle. This lead to the conclusion that the positive charge of the mass was concentrated in the center, the atomic nucleus!

See also

http://physicsbook.gatech.edu/Collisions for a general understanding of all collisions.

http://physicsbook.gatech.edu/inelastic_collisions to contrast them from elastic collisions.

Further reading

http://www.britannica.com/science/elastic-collision

External links

[1]

[2]

[3]

References

Main Idea:

Matter and Interactions, 4th Edition

http://www.sparknotes.com/testprep/books/sat2/physics/chapter9section4.rhtml

http://blogs.bu.edu/ggarber/archive/bua-physics/collisions-and-conservation-of-momentum/

History:

https://en.wikipedia.org/wiki/Elastic_collision

Connectedness:

http://www.iihs.org/

Additionally used references from see also.