Elastic Collisions

CLAIMED BY SEAN FISCHER

The Main Idea

So what exactly is an elastic collision? I know you’re thinking, “Oh I know all about elasticity,” but LOL this is not bubble gum or rubber bands guys!

An elastic collision is a collision between two or more objects in which there is no loss in kinetic energy before and after the collision. If we assume that the colliding objects are part of the system and that there is no force from the surroundings, the final kinetic energy is still in the same form as it was initially. To keep it simple, this means that kinetic energy in= kinetic energy out. Remember how your parents always told you what goes in must come out? They were talking about elastic collisions... probably.

Additionally, elastic collisions are a wonderful representation of the conservation of momentum which states that the momentum of an isolated system is constant. For an isolated system undergoing an elastic collision momentum in = momentum out.

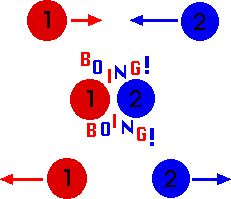
And I love playing pool because every time a ball hits another and they bounce off one another I’m witnessing an elastic collision so basically I’m a physicist in the lab. The image below demonstrates the main idea of an elastic collision. Boing!!

It's important to note that with macroscopic systems there are no perfectly elastic collisions because there's always at least a dab of dissipation (like some thermal energy given off), but most are nearly elastic. The only time there are perfect collisions is on a microscopic level when atomic systems with quantized energy collide, but that's only if there is enough energy available to raise the systems to an excited quantum state-- but quantum energy is really a whole other topic. Let's focus on elastic collisions!

Check out this funny video on elastic collisions also! https://www.youtube.com/watch?v=W9EqU1_DXUw

Now check out this more informative video on elastic collisions: https://www.youtube.com/watch?v=V4vzNk4qppw

A Mathematical Model

Now lets take what we know about elastic collisions and talk about it in mathematical terms. There are three main mathematical concepts surrounding elastic collisions:

---

---

Example Problem

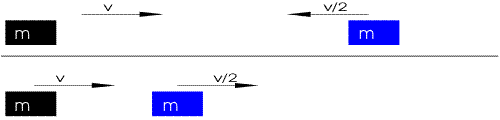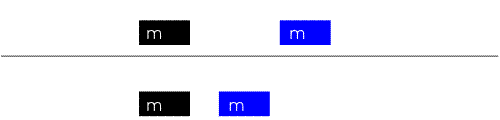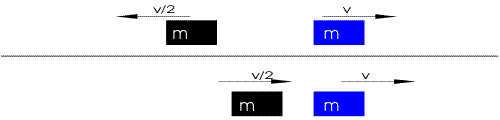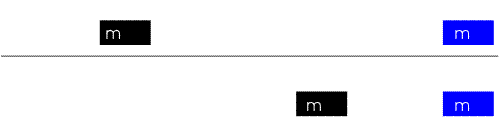
Cart 1, moving in the positive x direction, collides with cart 2 moving in the negative x direction. Both carts have identical masses and the collisions is (nearly) elastic, as it would be if the carts interacted magnetically or repelled each other through soft springs. What are the final momenta of the two carts?

1. After choosing a correct system, surroundings, and initial and final states, we can apply the momentum principle mentioned above to get a relationship between the initial and final momentums of the two carts.

2. Next, by applying the energy principle we can gain knowledge about the final and initial kinetic energies. By acknowledging the fact that the change in internal energy is 0 and the fact the reaction happens so quickly that not work or heat transfer is done by the surroundings, the equation can be simplified to include just initial and final kinetic energies.

3. Once we have simplified the momentum and energy principles, one can use the relationship between kinetic energy and momentum mentioned above to get a relationship involving both energy and momentum. Once this is obtained, the equation can be shifted around to get both the final momentums.

A Computational Model

The link below demonstrates a basic car crash elastic collision using MATLAB. Take note of the changes in displacement and the time.

Elastic Collision MATLAB model

Examples

Be sure to show all steps in your solution and include diagrams whenever possible. For a lot of the complicated problems, starting with a diagram and writing down the given information and plugging that into either the momentum or energy principle can help you move forward in the problem. If you still get stuck, try finding similar examples to that problem and look at the solutions to get on the right track.

Simple

Okay let’s start with a simple example like the ones you don't see on the test.

Jay and Sarah are best friends. Since they’re best friends they both weigh 55 kg. Jay hadn’t seen Sarah in a long time so when she saw her she ran to her with a velocity of <4,0,0> m/s. Instead of a hug, they were both too excited and collided and bounced back off of each other, and Sarah flew back with a velocity of <7,0,0> m/s. What was Jay’s final velocity?

In a lot of simple elastic collision problems, the momentum principle is all you need to solve them. Most problems will the initial velocities, masses, and one final velocity and you will be asked to solve for a either a final velocity or final momentum. By setting up an equation like the one in this problem, one can easily handle this type of problem.

Middling

When far apart, the momentum of a proton is <5.2 ✕ 10−21, 0, 0> kg · m/s as it approaches another proton that is initially at rest. The two protons repel each other electrically, but they are not close enough to touch. When they are far apart again later, one of the protons now has a velocity of <1.75, .82, 0> m/s. At that instant, what is the momentum of the other proton? HINT: Mass of proton is 1.7 *10^-21 kg.

A lot of people freak out when they see problems involving atomic particles and electrical forces, but the concept is the same no matter the scale. For this problem we are given masses, velocities, and momentum, but the equation p = mv allows us to easily handle these different values. Once again drawing a diagram helps to understand what is actually happening in the problem, making it easier to put the values in the correct places and solve.

Difficult

Okay, let's get a little bit trickier here...

There is a 400 kg train traveling at 55 m/s that collides, elastically of course, with a random 2 kg trashcan that's stationary on the tracks. So afterwards, what are the speeds of both the train and the trashcan after the collision?

This was a difficult problem because of the assumptions we had to make in order to solve it. Because the collision was elastic we were able to disregard the change in internal energy in the energy principle, and since it happened so quickly the work done by the track and heat transfer between the surroundings was negligible. It is tough to tell what assumptions you can make and which ones you can't in problems like these, which is what can make them difficult. On most exams or quizzes the collision problems will be inelastic simply because they are harder, but it is important to understand the fundementals of elastic collisions and how to solve problems involving them.

Real World Example

(Edit by Lakshmi Krishnan (lkrishnan7))

Now, let's look at a real world example of elastic collisions: car crashes.

Scenario: A woman is lying on the side of the road, appears to have been hit by a car.

Witness Statement: Witness says that there was a lady walking across the road and at the middle of the road, she paused for a second because she saw a car coming at her. The car was unable to stop in time, and hit the lady at a speed of 25 miles per hour, or around 10 metres per second. The witness also notes the layer of ice on the road.

Report: This is an example of the Law of Conservation of Momentum, which states that in the absence of an external force, there is conserved quantity of momentum, or

P initial = P final (where P = momentum)

MOMENTUM = M X V M1V1 + M2V2= M1U1 + M2U2 (M = mass , V1 and V2 = initial velocity of object 1 and 2, U1 and U2 = velocities after collision Essentially, the momentum that was lost by the car, is equal to the momentum gained by the lady. The lady would’ve had no velocity when the car hit her, and according to the law of conservation of momentum - whatever momentum you have at the start, you have at the end. This means that there would’ve been a redistribution of momentum between car and lady. The car will give some momentum to the lady... however, the car can’t give mass, so the only thing it can her give is velocity.

If we investigate further, we can see that this system was an isolated system. Normally, in collisions like these, we are not dealing with isolated systems... because that would mean that force is free from the influence of a net external force, or a force that can alter the momentum. Most of the time, friction between the car and the road, being an external force, would contribute to a change in total momentum. However, after observing the road, we can say that conditions were such that any external force (ie. friction and air resistance) was negligible, and thus, the total momentum of the two particles are conserved.

What we see here is a case of elastic collision - which means that there was no loss of kinetic energy. In an elastic collision, the objects “bounce” off each other, and don’t stick together to become one body - because this would be an inelastic collision, where part of the kinetic energy is changed to some other form of energy in the collision. But, as said before, this was an elastic collision, it would’ve looked something like this:

File:IMG 5563.JPG

It was noted that the car weighed 1600 kgs, while the woman weighs 50 kgs. The speed of the car was 10 metres/second, while the women's speed was 0 m/s (she stood still) We can figure out the velocities of both the woman and and the cars after the collision by deriving the formula

File:IMG5564.JPG

Velocities after the collision

V1 =[ M1 - M2 / (M1+ M2) ] V V2 = [ 2M1/ M1 + M2 ] V

• Conclusion: If we make a table, we can see the distribution of momentum.

Because of the fact that the mass of the second object (Lady) is much smaller compared to the mass of the first object (car), the person is thrown back at a relatively high velocity.

File:Wikitable.JPG

Some of the velocity of the bus was given to the lady, which caused her to go flying and land on the other side of the road. This is common of road traffic accident and this redistribution of momentum, in the form of velocity, is where part of her injury comes from.

Connectedness

So how are collisions connected to the real world? Collisions are all around us!

One main example is cars! Lots of car companies will purposely test and wreck cars to test collisions! Data is then sent to places like the Insurance Institute for Highway Safety where we can learn about car agility and more.

Another example of collisions in real life is billiards. This is one of the most accurate real life examples of elastic collisions. One ball hits another ball at rest, and if done right the first ball stops and transfers nearly all its kinetic energy into kinetic energy in the second ball.

Another example is hitting a baseball. Hitting a ball off the end or to close the hands of a bat will cause some vibrational energy from the collision, but if the ball catches the sweet spot the collision is very elastic, and you don't feel any vibration when you strike the ball.

History

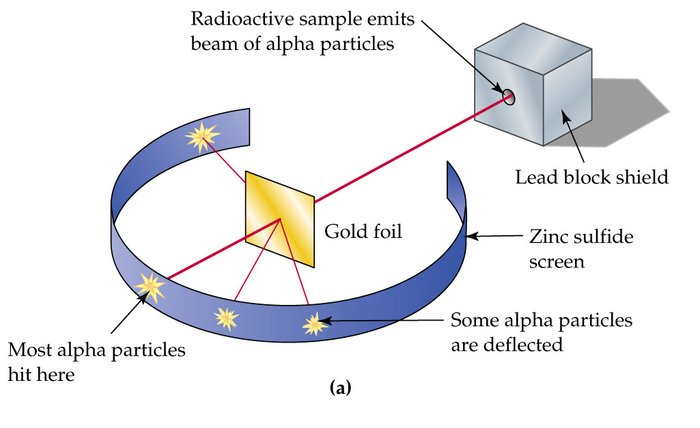
Collisions are certainly not a knew concept in the world. Ever since the beginning or time things have been colliding and reacting in different ways. It was experiments done by scientists like Newton or Rutherford that started to characterize collisions into categories and apply fundamental principles of physics to the reactions.

The history of collisions originates from the Rutherford Scattering experiment. As Rutherford studied the scattering of alpha particles through metal foils, he first noticed a collision with a single massive positive particle. This lead to the conclusion that the positive charge of the mass was concentrated in the center, the atomic nucleus!

See also

http://physicsbook.gatech.edu/Collisions for a general understanding of all collisions.

http://physicsbook.gatech.edu/inelastic_collisions to contrast them from elastic collisions.

Further reading

http://www.britannica.com/science/elastic-collision

External links

[1]

[2]

[3]

References

Main Idea:

Matter and Interactions, 4th Edition

http://www.sparknotes.com/testprep/books/sat2/physics/chapter9section4.rhtml

http://blogs.bu.edu/ggarber/archive/bua-physics/collisions-and-conservation-of-momentum/

History:

https://en.wikipedia.org/wiki/Elastic_collision

Connectedness:

http://www.iihs.org/

Additionally used references from see also.