Magnetic Field of a Solenoid Using Ampere's Law: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
If there are N loops of wire the compose a solenoid of length L, and we know that Ampere's Law for Magnetism gives us the form | If there are N loops of wire the compose a solenoid of length L, and we know that Ampere's Law for Magnetism gives us the form | ||
<math>{\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}}</math> | |||
This can be simplified to find that the magnitude if the magnetic field equals | This can be simplified to find that the magnitude if the magnetic field equals | ||
The direction can be found using the Right Hand | <math>BL=μ0NI</math> | ||
<math>{B = \frac{μ_{0}NI}{L}}</math> | |||
The direction can be found using the Right Hand Rule with your fingers curling around in the direction of the current and your thumb pointing in the direction of the magnetic field. It will always be along the axis for a solenoid. | |||
[[File:righthand.jpg]] | |||
===A Computational Model=== | ===A Computational Model=== | ||
Revision as of 17:59, 13 April 2016
---- CLAIMED BY JAKE WEBB 3/8/16 ----
Short Description of Topic
The Main Idea
A solenoid is a long coil of wire with a very small diameter, often used to make electromagnets due to their ability to create strong magnetic fields. The magnetic field can be easily calculated along the axis of the solenoid using Ampere's Law, and the magnitude and direction of the field is constant throughout the entirety of the solenoid, excluding the ends.
A Mathematical Model
If there are N loops of wire the compose a solenoid of length L, and we know that Ampere's Law for Magnetism gives us the form
[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]
This can be simplified to find that the magnitude if the magnetic field equals
[math]\displaystyle{ BL=μ0NI }[/math]
[math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]
The direction can be found using the Right Hand Rule with your fingers curling around in the direction of the current and your thumb pointing in the direction of the magnetic field. It will always be along the axis for a solenoid.
A Computational Model
Examples
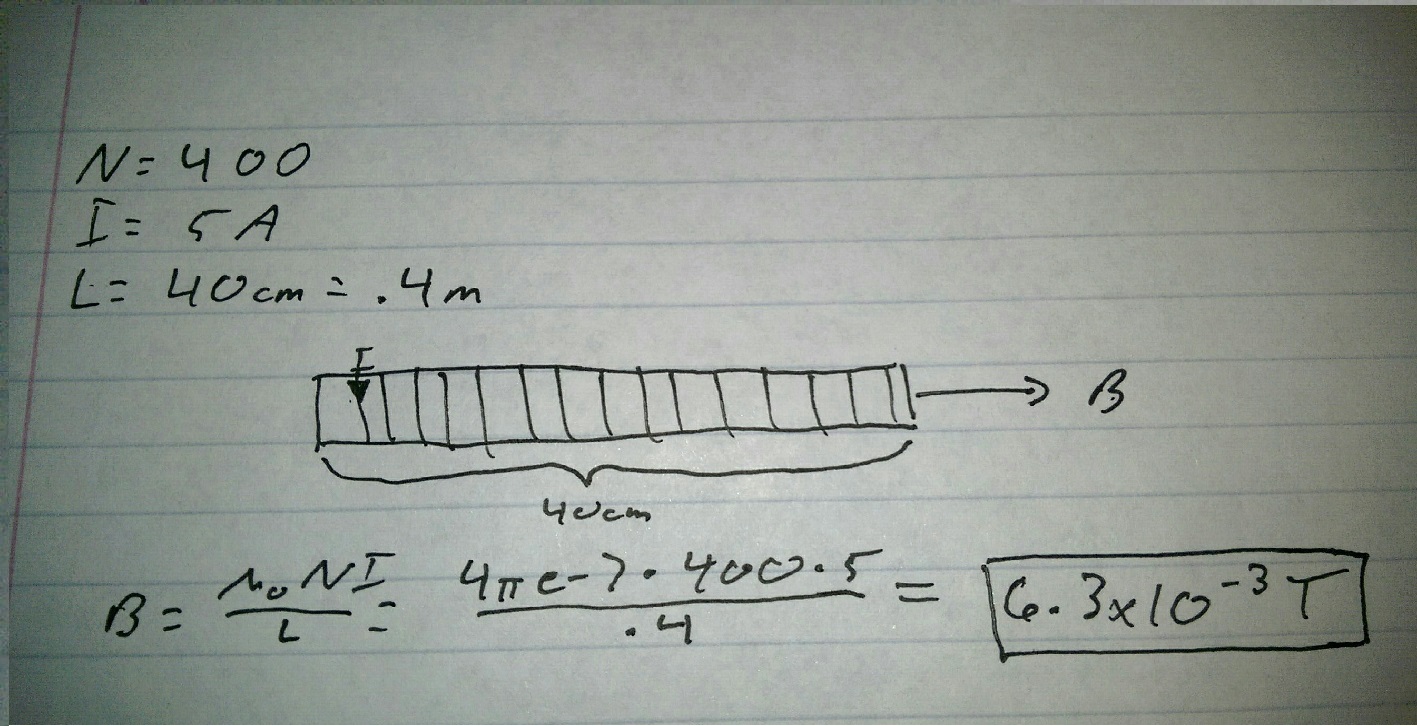
Simple
Find the magnetic field produced by the solenoid if the number of loops is 400 and current passing through on it is 5 A.( Length of the solenoid is 40cm)