Biot-Savart Law

CLAIMED BY JULIANNE OLIVER SPRING 2016 CLAIMED BY Rpatel401 FALL 2016

Magnetic field of a current carrying wire, a visual of a derivation of the Biot-Savart Law for currents. [1]

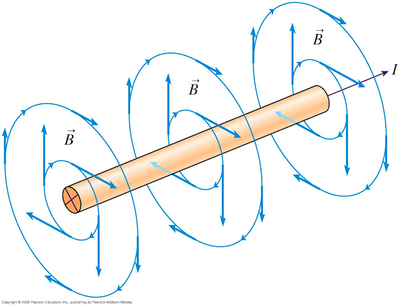
The Biot-Savart (pronounced bee-yo sahv-ar) Law is an equation that describes the quantitative relationship between a moving point charge and the magnetic field this moving point charge generates. This law is seen as the magnetic equivalent of Coulomb's Law (electric field of a point charge) [3], and this law states that the magnetic field decreases with the square of the distance from a moving point charge. The Biot-Savart Law is consistent with Ampere's Law and Gauss's Law for magnetism. The law is so named for Jean-Baptiste Biot and Felix Savart, who discovered the law in 1820.

The Main Idea

A moving point produces a magnetic field in addition to the electric fields created by point charges. In contrast to an electric field, a point charge must have some velocity in order to create a magnetic field.

A Mathematical Model

The general formula for a single point charge is [math]\displaystyle{ \vec B=\frac{\mu_0}{4\pi}\frac{q\vec v\times\hat r}{r^2} }[/math] where [math]\displaystyle{ \mu_0 }[/math] is the constant [math]\displaystyle{ 1e-7 \frac{tesla * m^2}{coloumb * \frac{m}{s}} }[/math] exactly. [math]\displaystyle{ \vec v }[/math] is the velocity of the point charge with charge [math]\displaystyle{ q }[/math], and [math]\displaystyle{ \hat r }[/math] is the unit vector pointing from the source location towards the observation location (remember [math]\displaystyle{ r= r(obs)-r(source) }[/math])

Direction of Magnetic Field: The direction of the magnetic field is not as simple as the direction of an electric field. The magnetic field's direction is given by crossing the velocity vector with the [math]\displaystyle{ \hat r }[/math] vector. The product of crossing two vectors is always a vector perpendicular to both of the original vectors! The cross product is at a maximum when the angle between the two vectors equals ninety degrees. The cross product is zero when two vectors are parallel to one another (the angle between the two vectors equals zero or 180).

A Special Note: When dealing with a moving electron, be sure to take into account the negative charge on the electron; this negative charge will switch the sign of the cross product between [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \hat r }[/math], due to the q in the Biot-Savart Law.

Magnitude of Magnetic Field: The magnitude of the magnetic field is given by [math]\displaystyle{ B=\frac{\mu_0}{4\pi}\frac{qv sin(\theta)}{r^2} }[/math]

A Computational Model

Check out this link: https://trinket.io/glowscript/93785debae for a look at a moving point charge acted on by a magnetic force. This magnetic force acts on the point charge since the point charge is moving with a certain velocity. Magnetic force goes hand-in-hand with magnetic field. Just as a point charge can only create a magnetic field if the point charge is moving, a point charge can only feel the force from a magnetic field if the point charge has a velocity. This computational model shows how a moving point charge, which creates its own magnetic field, is acted on by an external magnetic field.

For a computational model of a wire carrying current, see the wiki page on the Biot-Savart Law for Currents [[4]].

Examples

See below for solutions to these examples.

Example 1

An electron located at the origin is moving at [math]\displaystyle{ 2e8 }[/math] m/s in the +x direction. What is the magnetic field at [math]\displaystyle{ \lt 200, -300, 0\gt }[/math] m due to the moving electron?

Example 2

A proton is located on the +x axis and is moving with a velocity [math]\displaystyle{ \vec v }[/math] in the -y direction. What is the magnitude of the magnetic field due to the moving proton at [math]\displaystyle{ \lt 0, 0, z\gt }[/math] if the angle [math]\displaystyle{ \theta }[/math] between [math]\displaystyle{ \vec v }[/math] of the proton and [math]\displaystyle{ \hat r }[/math] equals 34 degrees?

Example 3

An electron located at the origin is moving with velocity [math]\displaystyle{ \vec velectron }[/math] in the +z direction. A proton is located directly in front of the electron and is moving with a velocity [math]\displaystyle{ \vec vproton }[/math] in the -y direction. What is the magnetic field at the location of the proton due to the moving electron?

Answers to Examples

Example 1:

Example 1

First, calculate [math]\displaystyle{ \vec r }[/math], which is [math]\displaystyle{ \vec r = \lt 200, -300, 0\gt -\lt 0,0,0\gt =\lt 200, -300, 0\gt }[/math] m. Using [math]\displaystyle{ \vec r }[/math], calculate [math]\displaystyle{ \hat r }[/math]: [math]\displaystyle{ \hat r = \frac{ \lt 200, -300, 0\gt }{\sqrt {200^2 + -300^2}}= \lt 0.554, -0.832, 0\gt }[/math]

Next, calculate [math]\displaystyle{ q \vec v }[/math]. Remember that an electron carries a negative charge: [math]\displaystyle{ -1.6e-19* \lt 2e8, 0, 0\gt = \lt -3.2e-11, 0, 0\gt }[/math]. Next, compute the cross product, [math]\displaystyle{ q\vec v\times\hat r }[/math]. The cross product is given as [math]\displaystyle{ \vec A\times\vec B = \lt AxBz - AzBy, AzBx - AxBz, AxBy-AyBz\gt }[/math] or by computing the determinant. The cross product in this case is [math]\displaystyle{ \lt 0, 0, 2.65e-11\gt }[/math].

Finally, divide [math]\displaystyle{ q\vec v\times\hat r }[/math] by the magnitude of [math]\displaystyle{ \vec r }[/math] squared: [math]\displaystyle{ \frac{ \lt 0, 0, 2.65e-11\gt }{360.55} = \lt 0, 0, 7.34e-14\gt }[/math]. Multiply by the constant [math]\displaystyle{ 1e-7 }[/math] given in the formula, and the final answer is [math]\displaystyle{ \vec B = \lt 0, 0, 7.34e-21\gt Teslas }[/math]

Example 2:

Example 2

First, as in example one, calculate [math]\displaystyle{ \vec r }[/math], and then the magnitude of [math]\displaystyle{ \vec r }[/math]. [math]\displaystyle{ \vec r = \lt 0, 0, z\gt - \lt x, 0, 0\gt = \lt -x, 0, z\gt }[/math]. The magnitude of [math]\displaystyle{ \vec r }[/math] is then [math]\displaystyle{ \sqrt{x^2 + z^2} }[/math]. We can then multiply the magnitudes of [math]\displaystyle{ q,\vec v, }[/math] and [math]\displaystyle{ sin }[/math] ([math]\displaystyle{ \theta }[/math]) to get the final answer:

[math]\displaystyle{ B = \frac{\mu_0}{4\pi}\frac{qvsin(34)}{(\sqrt{x^2 + z^2})^2} }[/math]

Example 3:

Example 3

As seen in the diagram, [math]\displaystyle{ \hat r }[/math] from the proton to the electron is parallel to the electron's velocity. Therefore, [math]\displaystyle{ \vec velectron\times\hat r }[/math] is zero because the two vectors are parallel ([math]\displaystyle{ \theta=0 }[/math] degrees).

Applications

Magnetic Response

The Biot-Savart law has applications in nuclear magnetic resonance (NMR) spectroscopy, used to measure the chemical signals given off by compounds. The law can be used to calculate the magnetic responses at the atomic or molecular level, provided that the current density can be obtained mathematically. For more about NMR spectroscopy, see the wiki page [5]

In this example,[2], the yellow arms represent whirring space from a black hole and the red lines represent vortex lines. Astrophysicists may use the Biot-Savart Law to calculate the velocity.

Aerodynamics

In aerodynamics, the Biot-Savart law may be used to calculate the velocity induced by vortex lines, which are lines that are everywhere tangent to the vorticity vector. A vorticity vector is a pseudovector field that describes the tendency of something to rotate; in other words, the vorticity vector is the curl of the velocity field of a fluid.

Medical Technology

Aside from applications in aerospace engineering and chemistry, the Biot-Savart law also plays an important role in magnetic resonance imaging (MRI). MRIs are a crucial piece of technology in the medical field; they are used for diagnosing cancer, detecting stress fractures, analyzing musculoskeletal injuries, and much more. An MRI machine is essentially one large magnetic field, and the hydrogen proton's axes in the human body all line up when a person is placed in an MRI. The magnetic field in an MRI is created by electric coils with moving electrons, which carry a current through the coils. This current is produced by exposing moving electrons to the electric field in the coils. if the moving electrons did not create magnetic fields, then no current would run through the coils, and MRIs would not exist.

History

Felix Savart was born on June 30, 1791 in Mezieres, France to a family with a strong association with military engineering schools. While completing his formal education in 1808 at the university in Metz, Savart decided to pursue medicine and become a physician. After serving a short stint in Napoleon's army in the the first engineering battalion, he resumed his medical training and graduated from Strasbourg in 1816. During his medical studies, Savart became interested in first century Roman writer Aulus Cornelius Celsus and his famous medical book De medicinia. Savart began working on a translation and set up a medical practice in Metz in 1817, but he gradually became more interested in physics rather than patients, particularly in sound and acoustics. He began building violins as a way to explore the form of the instrument through mathematical principles.

In 1819, Savart officially closed the doors of his medical practice and went to Paris to find a publisher for the translation of De medicina. While there, he attended a lecture on acoustics by Jean-Baptiste Biot at the Faculty of Sciences. The two met there and began collaboration, when in 1820, Hans Christian Oersted published his findings regarding a compass needle's behavior when placed near a current-carrying wire: the needle pointed at right angles to the wire. Biot and Savart began looking more closely into the field produced by a current-carrying wire, and by using the oscillation of a magnetic dipole to determine the strength of the field close to a current-carrying wire, they discovered what is now called the Biot-Savart Law [[6]].

See also

Right hand rule [[7]] Biot-Savart Law for Currents [[8]] Jean-Baptiste Biot [[9]].

External links

"Teach Engineering" on Biot-Savart [10] Derivation and Examples [11] Biot-Savart and Ampere's Law on MIT OpenCourse [12]

References

Matter & Interactions vol. II