Free Body Diagram: Difference between revisions

Revision as of 12:03, 16 April 2016

Claimed by Whitney Graham

Main Idea

A free body diagram, or force diagram, is a drawing of an object that is used to show all of the forces acting on the body. In mechanics, free body diagrams are extremely helpful because they allow visualization of each force acting upon the object. There are various forces that can be acting on the object, such as applied force, frictional force, normal force, and gravitational force. However, free body diagrams are not limited to these. All forces on a free body diagram are due to the body's interactions with its surroundings. Especially when problems become complicated and involve multiple different forces acting on more than one object, free body diagrams can be extremely effective in making a problem simpler to handle.

Points are commonly used to depict the system

Boxes are commonly used to depict the system

How To Draw a Free Body Diagram 1) Identify the system 2) List and identify all objects in the system's surroundings that interact with the system 3) Draw a diagram with the system at the center

Can use a dot to represent the system, OR
Can draw the details of the system

4) Draw all the forces acting on the system (represented as arrows). Arrow length should represent the approximate magnitude of that force relative to other forces 5) Label all forces with a symbol and identify them by the object causing the force 6) Break forces into their components as needed. (If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force).

Relation to Newton's Second Law Free body diagrams are usually used in collaboration with Newton's Second Law, F=mass*acceleration, as both are typically used in the process of solving for force. Newton's Second Law is the sum of the forces. The sum of the forces is equal to zero when the object is not accelerating or is moving at constant velocity.

Types of Forces to Consider for Free Body Diagrams Although all of these forces are not always present in every situation, some of these forces will usually be present acting on a system.

Applied Force: This is the force applied to the system by a person or other object.

Force of friction: This is the force that a surface applies on the system that is moving (or trying to move) on that surface.
- Important formula: f=μN f=frictional force N=normal force

Force of gravity: The force of gravity is the force that, on Earth, will act downward toward the center of the Earth.
- Important formula: Force of gravity=mg where m=mass g=9.8 m/s^2

Normal force: This is a force that is present when the system is on another object or surface, and the object or surface is exerting a force on the system as support.

Spring force: The spring force is a force that is exerted by a spring onto any system that is attached to it.
Important formula: Spring force=-kx where k=spring constant x=the displacement from the spring's relaxed position

Force of tension: This is the force that exists when a rope, string, wire, etc. is pulling on the system.

These are just the most common forces for free body diagrams in mechanics; however, other forces also exist.

Examples

Simple Example 1: A person rides in an elevator moving at constant velocity. Create a free body diagram to represent this situation.

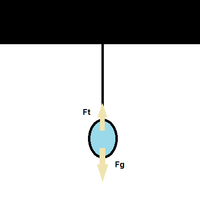
Example 1 Solution-In this example, the only forces acting on the system are the force of gravity and the normal force

Middling Example 2: A ball is hanging on a string of negligible mass from the ceiling. Create a free body diagram to model this situation.

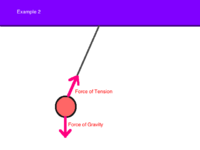
Example 2 Solution-In this example, the only forces acting on the system are the force of gravity and the force of tension

Note: For this example, when solving for forces, the force of tension must be split into horizontal and vertical components and solved.

Difficult Example 3: A stationary box lies on an incline. Create a free body diagram to model this situation.

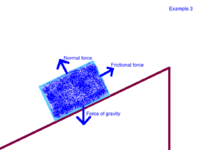
Example 3 Solution-In this example, the forces acting on this system are the force of gravity, the force of friction, and the normal force.

Note: Friction is necessary to keep the box stationary. When solving for the normal force and for frictional force, both the x and y component must be considered.

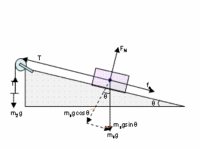
This, found from http://demos.smu.ca/index.php/demos/mechanics/141-free-body-diagram, is a more complicated problem to show that free body diagrams prove extremely helpful when sorting out problems with multiple different objects being acting upon.

Diagrams with solution are on the left and right.

Connectedness

While free body diagrams do not necessarily correlate with my life, they do have an application in the real world. For example, companies designing things such as billboards and even things such as houses, free body diagrams can be used to solve for how much force the structure must be supporting before construction begins.

History

References

http://demos.smu.ca/index.php/demos/mechanics/141-free-body-diagram

http://hyperphysics.phy-astr.gsu.edu/hbase/freeb.html

Matter and Interactions: Modern Mechanics. Volume One. 4th Edition.

https://www.wisc-online.com/learn/natural-science/physics/tp1502/construction-of-free-body-diagrams

@@ Line 7: / Line 7: @@
 [[File:Ya.png|200px|thumb|right|Points are commonly used to depict the system]]
 [[File:Boxx.png|200px|thumb|right|Boxes are commonly used to depict the system]]
 '''How To Draw a Free Body Diagram'''
-To create a free body diagram, it is most beneficial if the system and surroundings are identified, and any forces that are identified to be negligible do not need to be drawn on the diagram. A box or point is usually used to model the system in a free body diagram. Each force is typically represented by an arrow, which is drawn in the direction in which they act on the system. The size of each arrow, though not completely to scale, should mirror the magnitude of the force. Each of these arrows should be labeled as a certain force to avoid confusion when solving problems. Free body diagrams only take into account the forces directly acting on the object.
+) Identify the system
+) List and identify all objects in the system's surroundings that interact with the system
+) Draw a diagram with the system at the center
+*Can use a dot to represent the system, OR
+*Can draw the details of the system
+) Draw all the forces acting on the system (represented as arrows). Arrow length should represent the approximate magnitude of that force relative to other forces
+) Label all forces with a symbol and identify them by the object causing the force
+) Break forces into their components as needed. (If a force is acting diagonal to the system, create a dashed line parallel and perpendicular to the system and label it as the x and y components of that force).
 '''Relation to Newton's Second Law'''
-Free body diagrams are usually used in collaboration with Newton's Second Law, F=mass*acceleration, as both are typically used in the process of solving for force. Newton's Second Law is the sum of the forces. The sum of the forces is equal to zero when the object is not accelerating or is moving at constant velocity. Free body diagrams and the equation F=ma work together to help solve problems. The free body diagram does not change until another force starts or stops acting on it.
+Free body diagrams are usually used in collaboration with Newton's Second Law, F=mass*acceleration, as both are typically used in the process of solving for force. Newton's Second Law is the sum of the forces. The sum of the forces is equal to zero when the object is not accelerating or is moving at constant velocity.
@@ Line 39: / Line 41: @@
 These are just the most common forces for free body diagrams in mechanics; however, other forces also exist.
 == Examples ==