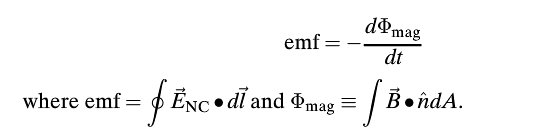Faraday's Law

Claimed by Cristina Guruceaga (cguruceaga3) Claimed by Amber Akbar to edit (Spring 2016)

Faraday's Law of Induction

Faraday's law focuses on how a time-varying magnetic field produces a "curly" non-Coulombic electric field, thereby inducing an emf.

Faraday's Law summarizes the ways voltage can be generated as a result of a time-varying magnetic flux. 

Faraday's law is one of four laws in Maxwell's equations. It tells us that in the presence of a time-varying magnetic field or current (which induces a time-varying magnetic field), there is an emf with a magnitude equal to the change in magnetic flux. It serves as a succinct summary of the ways a voltage (or emf) may be generated by a changing magnetic environment. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. It involves the interaction of charge with magnetic field.

Faraday's Law Experiment

Faraday showed that no current is registered in the galvanometer when bar magnet is stationary with respect to the loop. However, a current is induced in the loop when a relative motion exists between the bar magnet and the loop. In particular, the galvanometer deflects in one direction as the magnet approaches the loop, and the opposite direction as it moves away.

Faraday’s experiment demonstrates that an electric current is induced in the loop by changing the magnetic field. The coil behaves as if it were connected to an emf source. Experimentally it is found that the induced emf depends on the rate of change of magnetic flux through the coil.

Mathematical Equation

Faraday's Law Equation

In other words: The emf along a round-trip is equal to the rate of change of the magnetic flux on the area encircled by the path.

Direction: With the thumb of your right hand pointing in the direction of the -dB/dt, your fingers curl around in the direction of Enc.

The meaning of the minus sign: If the thumb of your right hand points in the direction of -dB/dt (that is, the opposite of the direction in which the magnetic field is increasing), your fingers curl around in the direction along which the path integral of electric field is positive. Similarly it can be explained using Lenz's Law. The direction of the induced current is determined by Lenz’s law which states that the induced current produces magnetic fields which tend to oppose the changes in magnetic flux that induces such currents.

Formal Version of Faraday's Law

Problem Solving Tips

To find the direction of the curly electric field, one must find the direction of [math]\displaystyle{ \frac{-dB}{dt} }[/math]. Do this using the change in magnetic field as the basis of finding the [math]\displaystyle{ \frac{-dB}{dt} }[/math].

The easiest way to do this is to imagine the a vector for the initial magnetic field, and a vector for the final magnetic field. Then, draw the change in magnetic field vector, [math]\displaystyle{ \Delta \mathbf{B} }[/math], and then the negative vector of that change in magnetic field gives [math]\displaystyle{ \frac{-dB}{dt} }[/math]. Pointing the thumb of your right hand in the direction of [math]\displaystyle{ \frac{-dB}{dt} }[/math] allows you to curl your fingers in the direction of [math]\displaystyle{ \mathbf{E_NC} }[/math].

In this chapter we have seen that a changing magnetic flux induces an emf:

according to Faraday’s law of induction. For a conductor which forms a closed loop, the emf sets up an induced current I =|ε|/R , where R is the resistance of the loop. To compute the induced current and its direction, we follow the procedure below:

1. For the closed loop of area on a plane, define an area vector A and let it point in the direction of your thumb, for the convenience of applying the right-hand rule later. Compute the magnetic flux through the loop using

Determine the sign of the magnetic flux

2. Evaluate the rate of change of magnetic flux . Keep in mind that the change could be caused by

Determine the sign of

3. The sign of the induced emf is the opposite of that of . The direction of the induced current can be found by using Lenz’s law or right hand rule (discussed previously).

Conceptual Question

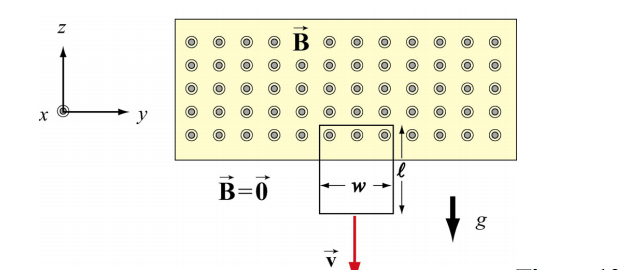
Falling Loop

A rectangular loop of wire with mass m, width w, vertical length l, and resistance R falls out of a magnetic field under the influence of gravity. The magnetic field is uniform and out of the paper within the area shown and zero outside of that area. At the time shown in the sketch, the loop is exiting the magnetic field at speed

1) What is the direction of the current flowing in the circuit at the time shown, clockwise or counterclockwise? Why did you pick this direction?

2) Using Faraday's law, find an expression for the magnitude of the emf in this circuit in terms of the quantities given. What is the magnitude of the current flowing in the circuit at the time shown?

3) Besides gravity, what other force acts on the loop in the ±k direction? Give its magnitude and direction in terms of the quantities given.

4) Assume that the loop has reached a “terminal velocity” and is no longer accelerating. What is the magnitude of that terminal velocity in terms of given quantities?

5) Show that at terminal velocity, the rate at which gravity is doing work on the loop is equal to the rate at which energy is being dissipated in the loop through Joule heating.

History

Michael Faraday was an English physicist working in the early 1800's. He worked with another scientist named Sir Humphrey Davy. Faraday's big discovery happened in 1831 when he found that when you change a magnetic field, you can create an electric current. He did a lot of other work with electricity such as making generators and experimenting with electrochemistry and electrolysis.

Faraday's experiments started with magnetic fields that stayed the same. That setup did not induce current. It was only when he started to change the magnetic fields that the current and voltage were induced (created). He discovered that the changes in the magnetic field and the size of the field were related to the amount of current created. Scientists also use the term magnetic flux. Magnetic flux is a value that is the strength of the magnetic field multiplied by the surface area of the device.

See also

To fully understand this topic, you need to have an understanding on Maxwell's equations and Lenz's Law.

Further reading

Maxwell, James Clerk (1881), A treatise on electricity and magnetism, Vol. II, Chapter III, §530, p. 178. Oxford, UK: Clarendon Press. ISBN 0-486-60637-6.

Kohlrausch, Friedrich (2005), The Fundamental Laws of Electrolytic Conduction: Memoirs by Faraday, Hittorf and F. Kohlrausch. ISBN: 9781297986291

External links

Faraday's Law Video Explanation: https://www.youtube.com/watch?v=fJjVxR2fynk

Faraday's Law Simulation: https://phet.colorado.edu/en/simulation/faradays-law

References

Encyclopedia.com: http://www.encyclopedia.com/topic/Faradays_law.aspx

Wikipedia (Electromagnetic Induction): http://en.wikipedia.org/wiki/Electromagnetic_induction

Encyclopædia Britannica (Faraday's Law of Induction): http://www.britannica.com/EBchecked/topic/201744/Faradays-law-of-induction