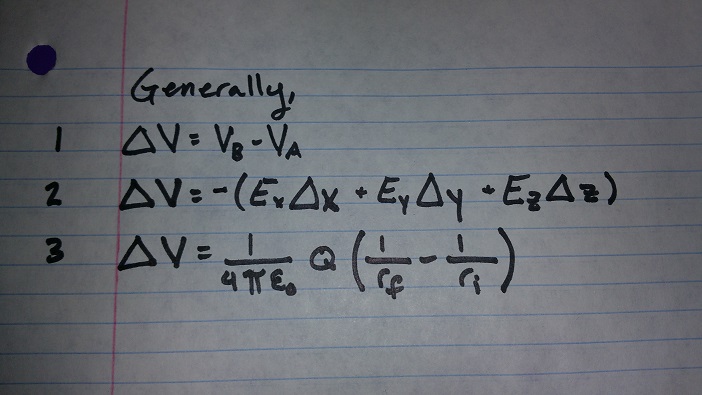Path Independence of Electric Potential

Claimed by Josh Whitley Spring 2016

When evaluating a change in electric potential, the path taken to get from point A to point B does not matter - all that matters is the initial state and final state.

The Main Idea

First, it is useful to define electric potential. Electric potential is the amount of electric potential energy that a point charge would have if it was located at some point in space (point B in this wiki page is how I will refer to this point in space), relative to an arbitrary reference point (point A). It equals the work done by a constant external force in carrying the charge from point A to point B. Note that this does mean moving a point charge around in space before returning it to its original location means both the work done and the potential equal 0. Electric potential is measured in volts or Joules/Coulomb. Electric potential at infinity is effectively 0.

Electric potential, as stated above, is entirely independent of the path taken to get from an initial to final state. When presented with a complex path from one point to another, choosing the easiest path (a straight line connecting the two points) can simplify the problem while still yielding the correct answer as a result of this principle.

Note that path independence holds true for all potential energy, not just electric potential. For that reason, a useful frame of reference is the path independence of physical objects' potential energy in a gravitic field that is introduced in physics 1 - electric potential path independence functions the same.

A Mathematical Model

Equation 1: This is a general representation of electric potential.

Equation 2: This is an expansion of the above equation - by summing the different components of the change in position within electric field components, you can calculate the change in electric potential. This equation is useful for proving path independence as it can be applied to multi-step path in straight line increments, proving when compared to a direct path that the change in electric potential is the same.

Equation 3: This is an example of a formula sheet formula adapted to show change in electric potential. It is essentially the same statement as equation 2, but specifically referencing the change in electric potential as you move through the electric field resulting from some point charge.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

alt text

Connectedness

1. How is this topic connected to something that you are interested in?

I was interested in this topic because this topic will be expanded to the topic of circuit. 

Since I have to study more about the circuit. I thought it would be helpful to understand the basic information for the future .

1. How is it connected to your major?

Since I am in mechanical engineering, I have to study broadly. 

Since the circuit is one of the topic that I have to take a course in Georgia Tech, Understanding this concept will help me to understand further about the circuit.

1. Is there an interesting industrial application?

To understand and to make the wire, it is necessary to understand 

how the potential difference in the wire has been built and how does that affect to the wire.

History

I could not find the history of the topic even if I tried to search on the internet spending about an hour.

See also

https://en.wikipedia.org/wiki/Voltage#See_also https://en.wikipedia.org/wiki/Electric_potential

Further reading

https://www.insidescience.org/content/soccers-electric-potential/1022 http://jes.ecsdl.org/content/147/11/4263.abstract

External links

http://farside.ph.utexas.edu/teaching/302l/lectures/node32.html http://faculty.cua.edu/sober/611/PATHIND.pdf

References

Matter & Interactions volume II by Ruth W. Chabay and Bruce A. Sherwood.