Magnetic Field: Difference between revisions
No edit summary |
No edit summary |
||
| Line 18: | Line 18: | ||
== characteristics of the Biot-Savart Law== | == characteristics of the Biot-Savart Law== | ||
[[File:Field3.JPG]] | [[File:Field3.JPG]] | ||
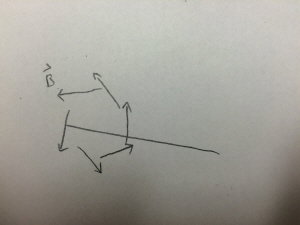
Because the equation involves the cross product of velocity and the position vector, one can find out that there is no magnetic field in the direction of the movement of the charged particle, because the cross product of two vectors in the same direction is zero. | Because the equation involves the cross product of velocity and the position vector, one can find out that there is no magnetic field in the direction of the movement of the charged particle, because the cross product of two vectors in the same direction is zero. | ||
| Line 23: | Line 26: | ||
[[File:Field2.JPG]] | [[File:Field2.JPG]] | ||
However, even in the absence of a magnetic field, an electric field may still be present. | However, even in the absence of a magnetic field, an electric field may still be present. | ||
By using a compass, one can calculate the magnitude of a current. The Earth exerts a magnitude that always points to the North. When a compass is near a current with a magnetic field, the needle would be deflected by the net magnetic field. Notice that although the magnetic field of the current is perpendicular to the direction of the movement of charges, the needle is not deflected 90 degrees because of the magnetic field of the Earth, which is usually larger than that of the current. | By using a compass, one can calculate the magnitude of a current. The Earth exerts a magnitude that always points to the North. When a compass is near a current with a magnetic field, the needle would be deflected by the net magnetic field. Notice that although the magnetic field of the current is perpendicular to the direction of the movement of charges, the needle is not deflected 90 degrees because of the magnetic field of the Earth, which is usually larger than that of the current. Also, because the magnetic field is exerted in a circular pattern, the direction of the magnetic field above the source is exactly the opposite of the magnetic field under the source. As a result, depending on the location of the compass, the needle may deflect in the opposite direction but with the same magnitude.[[File:field4.JPG]] | ||
Revision as of 20:11, 17 April 2016
Claimed by Seongshik Kim spring 2016
This page discusses the general properties and characteristics of magnetic fields
Magnetic Field
Unlike electric fields, magnetic fields are made by moving charges. Stationary charges do not exert magnetic fields. In equilibrium, there is no net motion of charges inside a metal. Therefore, it should be noted that electrons inside a metal must move continuously. This is the very basic definition of the current, a non-equilibrium system in which there is a constant flow of electrons in order to create a magnetic field.
There are a few important main concepts to understand before proceeding further. First, the direction of the magnetic field is perpendicular to the direction of the current. Second, equilibrium and being continuous are totally different things.
A Mathematical Model
The magnetic field created by a single charged particle is given by the equation [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{(q\vec{v} \times \hat{r})}{|\vec{r}|^2} }[/math], where [math]\displaystyle{ \frac{\mu_0}{4\pi} }[/math], where [math]\displaystyle{ \frac{\mu_0}{4\pi} }[/math] is a fundamental constant equal to [math]\displaystyle{ 1 \times 10^{-7} T }[/math], [math]\displaystyle{ q }[/math] is the charge of the particle, [math]\displaystyle{ \vec{v} }[/math] is the velocity of the particle, and [math]\displaystyle{ \vec{r} }[/math] is the vector that points from source to observation location. This equation is called the Biot-Savart law. You may notice that this equation involves a cross product.
characteristics of the Biot-Savart Law
Because the equation involves the cross product of velocity and the position vector, one can find out that there is no magnetic field in the direction of the movement of the charged particle, because the cross product of two vectors in the same direction is zero.
However, even in the absence of a magnetic field, an electric field may still be present.
By using a compass, one can calculate the magnitude of a current. The Earth exerts a magnitude that always points to the North. When a compass is near a current with a magnetic field, the needle would be deflected by the net magnetic field. Notice that although the magnetic field of the current is perpendicular to the direction of the movement of charges, the needle is not deflected 90 degrees because of the magnetic field of the Earth, which is usually larger than that of the current. Also, because the magnetic field is exerted in a circular pattern, the direction of the magnetic field above the source is exactly the opposite of the magnetic field under the source. As a result, depending on the location of the compass, the needle may deflect in the opposite direction but with the same magnitude.
== Dependence on frame of reference== ([math]\displaystyle{ \vec{v} = 0 }[/math])
Magnetic field due to a single charged particle
The magnetic field [math]\displaystyle{ \vec{B} }[/math] created by a single charged particle is given by the equation [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{(q\vec{v} \times \hat{r})}{|\vec{r}|^2} }[/math], where [math]\displaystyle{ \frac{\mu_0}{4\pi} }[/math] is a fundamental constant equal to [math]\displaystyle{ 1 \times 10^{-7} T }[/math], [math]\displaystyle{ q }[/math] is the charge of the particle, [math]\displaystyle{ \vec{v} }[/math] is the velocity of the particle, and [math]\displaystyle{ \vec{r} }[/math] is the vector that points from source to observation location. This equation is called the Biot-Savarde law. You may notice that this equation involves a cross product.
Page initiated by --Spennell3 (talk) 14:20, 19 October 2015 (EDT)