Escape Velocity: Difference between revisions
Tdellaert3 (talk | contribs) No edit summary |
Tdellaert3 (talk | contribs) (Changed the opening image from an erroneous picture of a SpaceX rocket. Reworded the entire "Main Idea" section. Added captions to the energy diagrams and completely rewrote the explanatory text. Removed an empty section on computational models.) |
||
| Line 1: | Line 1: | ||
[[File:Escape-velocity-diagram.gif|400px|thumb|right| A diagram showing several orbits around Earth. Orbit ''p'' is a parabolic orbit, with the object travelling at escape velocity. Orbit ''H'' is an example of the hyperbolic orbit of an object travelling faster than the escape velocity.]] | |||
[[File: | |||
Escape velocity is defined as the minimum velocity required for an object to escape the gravitational force of a large object. The sum of an object's kinetic energy and its gravitational potential energy is equal to zero. The gravitational potential energy is negative due to the fact that kinetic energy is always positive. The velocity of the object will be be zero at infinite distance from the center of gravity. There is no net force on an object as it escapes and zero acceleration is perceived. | |||
==The Main Idea== | ==The Main Idea== | ||
The formula for escape velocity at a | The formula for escape velocity at a givendistance from a body is calculated by the formula | ||
:<math>v_e = \sqrt{\frac{2GM}{r}},</math> | :<math>v_e = \sqrt{\frac{2GM}{r}},</math> | ||
| Line 16: | Line 12: | ||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
When we model escape velocity | When we model escape velocity, we consider the situation when an object's velocity takes it to a point an infinite distance away. The lowest possible escape velocity has a final speed of zero, and any speed higher results in a nonzero final speed. To derive the formula for the escape velocity, the energy principle is used, and we assume that the only two objects in our system are the orbiting body and the planet. | ||
In our system , the energy principle states that | |||
:<math>(K + U_g)_i = (K + U_g)_f \,</math> | :<math>(K + U_g)_i = (K + U_g)_f \,</math> | ||
''K''<sub>''ƒ''</sub> = 0 because final velocity | When finding the minimum escape velocity, ''K''<sub>''ƒ''</sub> = 0 because we take the final velocity to be zero, and ''U''<sub>gƒ</sub> = 0 because its final distance is expressed as infinity, therefore | ||
:<math>\frac{1}{2}mv_e^2 + \frac{-GMm}{r} = | :<math>(K + U_g)_i = \frac{1}{2}mv_e^2 + \frac{-GMm}{r} = 0</math> | ||
< | Solving for ''v''<sub>''e''</sub> yields: | ||
:<math>v_e = \sqrt{\frac{2GM}{r}}</math> | :<math>v_e = \sqrt{\frac{2GM}{r}}</math> | ||
Note that because both the kinetic and potential energy terms contain a common factor ''m'', the final escape velocity is independent of the mass of the orbiting body. | |||
===Bound versus unbound systems=== | |||
When an object is orbiting a massive body, it can be in one of two states: bound and unbound. If the object is in a bound state, we see an elliptical trajectory, in which the orbiting body never escapes the gravitational influence of the more massive body. In an unbound state, however, we observe a parabolic or hyperbolic trajectory, in which the object is able to escape the gravitational influence of the orbiting body and escape to infinity. The diagram to the left shows an unbound system, in which the sum of the kinetic and potential energy of the orbiting body is greater then 0. As distance goes to infinity in this system, gravitational potential energy approaches zero, but the object retains a positive kinetic energy, and therefore a positive velocity. The image on the right shows a bound system, in which the sum of the kinetic and potential energy is negative. In this system, kinetic energy reaches zero at a specific maximum distance, at which point the object begins to fall back towards the massive body, never to escape. | |||
[[File:Ediagram_MSPaint_UnboundSystemWithExtraEnergy.png|500px|thumb|left| | |||
< | [[File:Ediagram_MSPaint_UnboundSystemWithExtraEnergy.png|500px|thumb|left|The energy diagram of an unbound system, in which the object has excess kinetic energy. The vertical axis represents energy, while the horizontal axis represents distance. At exactly the escape velocity, the sum of <math>K</math> and <math>U</math> is exactly 0.]] | ||
[[File:EDiagram_MSPaint_BoundSystem.png|500px|thumb|right|The energy diagram of a bound system, in which the object has insufficient kinetic energy to escape. The vertical axis represents energy, while the horizontal axis represents distance. ]] | |||
<br clear=all> | |||
==Examples== | ==Examples== | ||
| Line 47: | Line 48: | ||
\Delta E = 0\\ | \Delta E = 0\\ | ||
v_i = ?\\ | v_i = ?\\ | ||
v_f = 0 m/s\\ | v_f = 0 \text{m/s}\\ | ||
r_i = | r_i = 71500\times 10^3 \text{m}\\ | ||
r_f = \infty\\ | r_f = \infty\\ | ||
m = | m = m_{Object}\\ | ||
M = | M = m_{Jupiter} = 1900\times 10^{24} \text{kg} \\ | ||
</math> | </math> | ||
| Line 62: | Line 62: | ||
\Delta E = W + Q\\ | \Delta E = W + Q\\ | ||
\Delta E = | \Delta E = 0 + 0 = 0\\ | ||
\Delta K + \Delta U = 0\\ | |||
\frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ | \frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ | ||
\frac{1}{2}m | \frac{1}{2}m(0-v_i^2) + (0 - \frac{-GMm}{r_i}) = 0\\ | ||
\frac{ | -\frac{1}{2}mv_i^2 + \frac{GMm}{r_i} = 0\\ | ||
\frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ | \frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ | ||
\frac{GM}{r_i} = \frac{1}{2}v_i^2\\ | \frac{GM}{r_i} = \frac{1}{2}v_i^2\\ | ||
v_i = \sqrt{\frac{2GM}{r_i}}\\ | v_i = \sqrt{\frac{2GM}{r_i}}\\ | ||
= \sqrt{\frac{2(6. | = \sqrt{\frac{2(6.7\times 10^{-11} )(1900\times 10^{24} \text{kg})}{(71500\times 10^3 \text{m})}}\\ | ||
= 59672.767m/s | = 59672.767m/s | ||
</math> | </math> | ||
Revision as of 21:05, 17 April 2016
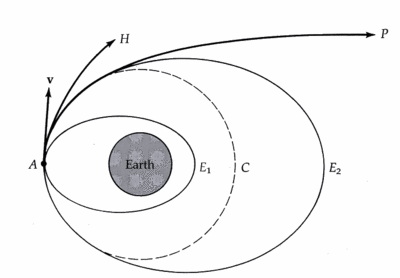
Escape velocity is defined as the minimum velocity required for an object to escape the gravitational force of a large object. The sum of an object's kinetic energy and its gravitational potential energy is equal to zero. The gravitational potential energy is negative due to the fact that kinetic energy is always positive. The velocity of the object will be be zero at infinite distance from the center of gravity. There is no net force on an object as it escapes and zero acceleration is perceived.
The Main Idea
The formula for escape velocity at a givendistance from a body is calculated by the formula
- [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}}, }[/math]
where G is the universal gravitational constant (G = 6.67×10−11 m3 kg−1 s−2), M is the mass of the large body to be escaped, and r the distance from the center of mass of the mass M to the object.<ref group="nb"> This equation assumes there is no atmospheric friction and is an ideal scenario with sending an object on a trajectory. In fact, the escape velocity stated here should actually be called escape speed due to the fact that the quantity to be calculated is completely independent of direction. Notice that the equation does not include the mass of the object escaping a large body as escape velocity is only dependent on gravitational force. We also assume that an object is escaping from a uniform body.
A Mathematical Model
When we model escape velocity, we consider the situation when an object's velocity takes it to a point an infinite distance away. The lowest possible escape velocity has a final speed of zero, and any speed higher results in a nonzero final speed. To derive the formula for the escape velocity, the energy principle is used, and we assume that the only two objects in our system are the orbiting body and the planet.
In our system , the energy principle states that
- [math]\displaystyle{ (K + U_g)_i = (K + U_g)_f \, }[/math]
When finding the minimum escape velocity, Kƒ = 0 because we take the final velocity to be zero, and Ugƒ = 0 because its final distance is expressed as infinity, therefore
- [math]\displaystyle{ (K + U_g)_i = \frac{1}{2}mv_e^2 + \frac{-GMm}{r} = 0 }[/math]
Solving for ve yields:
- [math]\displaystyle{ v_e = \sqrt{\frac{2GM}{r}} }[/math]
Note that because both the kinetic and potential energy terms contain a common factor m, the final escape velocity is independent of the mass of the orbiting body.
Bound versus unbound systems
When an object is orbiting a massive body, it can be in one of two states: bound and unbound. If the object is in a bound state, we see an elliptical trajectory, in which the orbiting body never escapes the gravitational influence of the more massive body. In an unbound state, however, we observe a parabolic or hyperbolic trajectory, in which the object is able to escape the gravitational influence of the orbiting body and escape to infinity. The diagram to the left shows an unbound system, in which the sum of the kinetic and potential energy of the orbiting body is greater then 0. As distance goes to infinity in this system, gravitational potential energy approaches zero, but the object retains a positive kinetic energy, and therefore a positive velocity. The image on the right shows a bound system, in which the sum of the kinetic and potential energy is negative. In this system, kinetic energy reaches zero at a specific maximum distance, at which point the object begins to fall back towards the massive body, never to escape.


Examples

Escaping Jupiter's Atmosphere
The radius of Jupiter is 71500e3 m, and its mass is 1900e24 kg. What is the escape speed of an object launched straight up from just above the atmosphere of Jupiter?
System = Jupiter + object [math]\displaystyle{ \Delta E = 0\\ v_i = ?\\ v_f = 0 \text{m/s}\\ r_i = 71500\times 10^3 \text{m}\\ r_f = \infty\\ m = m_{Object}\\ M = m_{Jupiter} = 1900\times 10^{24} \text{kg} \\ }[/math]
Starting from the Energy Principle:
[math]\displaystyle{ \Delta E = W + Q\\ \Delta E = 0 + 0 = 0\\ \Delta K + \Delta U = 0\\ \frac{1}{2}m(v_f^2-v_i^2) + (\frac{-GMm}{r_f} - \frac{-GMm}{r_i}) = 0\\ \frac{1}{2}m(0-v_i^2) + (0 - \frac{-GMm}{r_i}) = 0\\ -\frac{1}{2}mv_i^2 + \frac{GMm}{r_i} = 0\\ \frac{GMm}{r_i} = \frac{1}{2}mv_i^2\\ \frac{GM}{r_i} = \frac{1}{2}v_i^2\\ v_i = \sqrt{\frac{2GM}{r_i}}\\ = \sqrt{\frac{2(6.7\times 10^{-11} )(1900\times 10^{24} \text{kg})}{(71500\times 10^3 \text{m})}}\\ = 59672.767m/s }[/math]
Connectedness
In space, a rocket will not actually be able to travel an infinite distance once it escapes the gravitational pull of Earth, but rather must escape the gravitational pull of the Sun, the planets in our solar system, and every other larger body. The calculation of escape velocity assumes many conditions and cannot be completely applied to real life. However, if a spacecraft does not overcome the gravitational force of Earth, it will not be able to escape Earth and would likely fall back to Earth with disaster as there are many other conditions of leaving the atmosphere. The concept of escape velocity is very closely tied to the energy principle, and it is a direct application of conversion from potential to kinetic energies that is easily observable and testable. Application of this principle is most tied to aerospace and specifically spaceflight, but the underlying principle is a cross-discipline, universal concept.
External links
http://www.scientificamerican.com/article/bring-science-home-reaction-time/
https://www.youtube.com/watch?v=7w56rwAtUZU
References
"Escape Velocity | Physics." Encyclopedia Britannica Online. Encyclopedia Britannica, n.d. Web. 05 Dec. 2015. [1]
Giancoli, Douglas C. "Physics for Scientists and Engineers with Modern Physics." Google Books. Google, n.d. Web. 05 Dec. 2015. [2]
"Escape Velocity." Wikipedia. Wikimedia Foundation, n.d. Web. 05 Dec. 2015. [3]
Velocity, Escape, and ©200. ESCAPE VELOCITY EXAMPLES (n.d.): n. pag. 13 June 2003. Web. 5 Dec. 2015. [4]