Bar Magnet: Difference between revisions
Shisamuddin3 (talk | contribs) No edit summary |
m (Typos) |
||
| Line 2: | Line 2: | ||
claimed by Samah | claimed by Samah | ||
A bar magnet creates a magnetic field, just like many other | A bar magnet creates a magnetic field, just like many other device (i.e. a current carrying wire), however, it has a different pattern of magnetic field which we will explore. | ||
__TOC__ | __TOC__ | ||
| Line 15: | Line 15: | ||
---- | ---- | ||
In physics it is important to keep track of your frame of reference. Treat an effect as if it is arising at the source location and ending at the observation location. The source location marks the beginning point for an effect. The result of the effect is gauged at the observation location. | In physics, it is important to keep track of your frame of reference. Treat an effect as if it is arising at the source location and ending at the observation location. The source location marks the beginning point for an effect. The result of the effect is gauged at the observation location. | ||
Due to the fact that an observation location can either be on the axis of the magnet, or off the axis of the magnet, we have | Due to the fact that an observation location can either be on the axis of the magnet, or off the axis of the magnet, we have two different equations. Given a bar magnet with magnetic dipole moment μ, if the observation location is on the same axis as the magnet, assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles, we find that: | ||
<math> B = \frac{\mu _{0}}{4\pi }\cdot \frac{2\mu }{r^{3}}</math> | <math> B = \frac{\mu _{0}}{4\pi }\cdot \frac{2\mu }{r^{3}}</math> | ||
If the observation location is not on the axis of the bar magnet, and assuming that the distance from the observation location to the magnet is | If the observation location is not on the axis of the bar magnet, and assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles, we conclude that: | ||
<math> B = \frac{\mu _{0}}{4\pi }\cdot \frac{\mu }{r^{3}}</math> | <math> B = \frac{\mu _{0}}{4\pi }\cdot \frac{\mu }{r^{3}}</math> | ||
| Line 27: | Line 27: | ||
[[File:VFPt cylindrical magnet thumb.svg|thumb|left|The curly magnetic field of a bar magnet.]] | [[File:VFPt cylindrical magnet thumb.svg|thumb|left|The curly magnetic field of a bar magnet.]] | ||
As you can see in this picture, the magnetic field of a bar magnet takes the exact same form as an electric field of a dipole. The magnetic lines flow out of the north pole | As you can see in this picture, the magnetic field of a bar magnet takes the exact same form as an electric field of a dipole. The magnetic lines flow out of the north pole of the magnet, and into the south pole of the magnet, in a curling fashion. However, the 'poles' are merely just conventions. They do not represent anything, and are terms assigned to each end, but it is true that the magnetic field will always flow out of the 'north' end. The Earth itself can also be represented by the computational model of a bar magnet; however, there are a few misconceptions about this. For starters, the magnetic North Pole is actually located near the geographic South Pole, and the magnetic South Pole is located near the geographic North Pole. Furthermore, the magnetic poles are off axis, meaning the are not directly at the top and bottom of the Earth. There is a difference of almost 1.5 degrees! | ||
It is also interesting to note that just because this illustration depicts the bar magnet as having two distinct ends, if you were to cut the magnet down the middle | It is also interesting to note that just because this illustration depicts the bar magnet as having two distinct ends, if you were to cut the magnet down the middle, it would polarize in such a way that you would end up with two bar magnets, not a single south pole and a single north pole. | ||
| Line 36: | Line 36: | ||
This picture depicts the magnetic field based on the dipoles of the magnet. The north end is | This picture depicts the magnetic field based on the dipoles of the magnet. The north end is the left side of the magnet and the south end is the right side of the magnet. The field follows the direction from the north side to the south side of the magnet. | ||
== '''Examples''' == | == '''Examples''' == | ||
---- | ---- | ||
'''Example 1''': If a bar magnet is located at the origin | '''Example 1''': If a bar magnet is located at the origin with its North end aligned with the positive X-axis, what are the directions of the magnetic field at the following observation locations: above, below, to the left, to the right, and in a plane that is above the magnet? | ||
We already know that the field of a bar magnet flows out of the north end and into the south end in a curling fashion. So, using the diagram above, it is easy to see that to the right of the magnet, the direction of the magnetic field points in the +X direction. At a position to the left of the magnet, the field is flowing back into the south end of the magnet, so the direction of the magnetic field at this location is also in the +X direction. | |||
The field above and below the magnet is flowing from the right to the left at both locations, so the direction of the magnetic field above and below the magnet is in the -X direction. | The field above and below the magnet is flowing from the right to the left at both locations, so the direction of the magnetic field above and below the magnet is in the -X direction. | ||
At a different plane (z | At a different plane (z ≠ 0), there is no magnetic field, because we can assume that bar magnet acts as a 2-D dipole. | ||
'''Example 2:''' A bar magnet with magnetic dipole moment 0.58 lies on the negative x axis, as shown in the figure below. A compass is located at the origin. Magnetic north is in the negative z direction. Between the bar magnet and the compass is a coil of wire of radius 3.5 cm, connected to batteries not shown. The distance from the center of the coil to the center of the compass is 9.6 cm. The distance from the center of the bar magnet to the center of the compass is 23.0 cm. A steady current of 0.96 A runs through the coil. Conventional current runs clockwise in the coil when viewed from the location of the compass. Despite the presence of the magnet and coil the compass still points north. | '''Example 2:''' A bar magnet with magnetic dipole moment 0.58 A∙m<sup>2</sup> lies on the negative x axis, as shown in the figure below. A compass is located at the origin. Magnetic north is in the negative z direction. Between the bar magnet and the compass is a coil of wire of radius 3.5 cm, connected to batteries not shown. The distance from the center of the coil to the center of the compass is 9.6 cm. The distance from the center of the bar magnet to the center of the compass is 23.0 cm. A steady current of 0.96 A runs through the coil. Conventional current runs clockwise in the coil when viewed from the location of the compass. Despite the presence of the magnet and coil, the compass still points north. | ||
'''(a)''' Which | '''(a)''' Which pole of the bar magnet is closer to the compass? | ||
'''(b)''' How many turns of wire are in the coil? | '''(b)''' How many turns of wire are in the coil? | ||
'''Part A:''' Because the conventional current runs clockwise in the coil, you can use right hand rule to determine what direction the magnetic field is due to the coil. This tells us that the magnetic field due to the coil is in the -X direction. In order for the compass to stay still, the magnet needs to directly oppose the magnetic field of the coil, meaning its magnetic field has to point in the +X direction, meaning the ''' | '''Part A:''' Because the conventional current runs clockwise in the coil, you can use right hand rule to determine what direction the magnetic field is due to the coil. This tells us that the magnetic field due to the coil is in the -X direction. In order for the compass to stay still, the magnet needs to directly oppose the magnetic field of the coil, meaning its magnetic field has to point in the +X direction, meaning the '''north pole''' would have to be nearer the compass. | ||
'''Part B:''' Because the field created by the coil | '''Part B:''' Because the magnetic field created by the coil is equal to the magnetic field created by the magnet, we can set their two fields equal to each other: | ||
<math> \frac{\mu _{0}}{4 \pi } \cdot \frac{2\mu }{r^{3}} = \frac{\mu _{0}}{4 \pi } \cdot \frac{2NI\pi R^{2}}{(z^{2}+R^{2})^{3/2}} </math> | <math> \frac{\mu _{0}}{4 \pi } \cdot \frac{2\mu }{r^{3}} = \frac{\mu _{0}}{4 \pi } \cdot \frac{2NI\pi R^{2}}{(z^{2}+R^{2})^{3/2}} </math> | ||
Rearranging to solve this equation for N, we get: <math> N = \frac{\mu (z^{2}+R^{2})^{3/2}}{I\pi R^{2} d^{3}} </math> | Rearranging to solve this equation for N, we get: <math> N = \frac{\mu (z^{2}+R^{2})^{3/2}}{I\pi R^{2} d^{3}} </math> | ||
Plugging in .58 the magnetic dipole moment | Plugging in .58 A∙m<sup>2</sup> (the magnetic dipole moment, μ), .096 meters for z, .035 meters for R, .96 Amps for I, and .23 meters for d, we get that the number of loops in the coil is '''14'''. | ||
== '''Connectedness''' == | == '''Connectedness''' == | ||
---- | ---- | ||
[[File:Series L0.JPG|thumb|left|An experimental MAGLEV train created by Japanese engineers.]] | [[File:Series L0.JPG|thumb|left|An experimental MAGLEV train created by Japanese engineers.]] | ||
One very interesting applications of magnets is their ability to levitate objects. This is the main driving force in the case of MAGLEV trains. Magnetic levitation, or MAGLEV trains, hover above a long series of magnets where the magnets on the bottom of the train repel the magnets on the tracks below it. Sending an electric current through the coils on the bottom of the track allows the train to levitate a few inches off the ground, and propelling the current through the guided coils on the bottom of the track propels the train forward at unbelievable speeds (up to 250 MPH! | One very interesting applications of magnets is their ability to levitate objects. This is the main driving force in the case of MAGLEV trains. Magnetic levitation, or MAGLEV trains, hover above a long series of magnets where the magnets on the bottom of the train repel the magnets on the tracks below it. Sending an electric current through the coils on the bottom of the track allows the train to levitate a few inches off the ground, and propelling the current through the guided coils on the bottom of the track propels the train forward at unbelievable speeds (up to 250 MPH)! | ||
Making the train levitate is a useful tool because it reduces the amount of friction between the wheels and the track, and it allows for less fossil fuels to be used in order to make the train propel forwards. | Making the train levitate is a useful tool because it reduces the amount of friction between the wheels and the track, and it allows for less fossil fuels to be used in order to make the train propel forwards. | ||
| Line 72: | Line 72: | ||
[[File:img.jpg|thumb|left|MRI of brain.]] | [[File:img.jpg|thumb|left|MRI of brain.]] | ||
Magnetism is also used in medical technology. Medical | Magnetism is also used in medical technology. Medical Resonance Imaging (MRI) machines use magnetic fields and radio waves to create images of the body. | ||
| Line 81: | Line 81: | ||
---- | ---- | ||
[[File:James Clerk Maxwell.png|thumb|right|James Clerk Maxwell]] | [[File:James Clerk Maxwell.png|thumb|right|James Clerk Maxwell]] | ||
The first magnets were not invented, but rather discovered. The ancient Greeks and ancient Chinese | The first magnets were not invented, but rather discovered. The ancient Greeks and ancient Chinese stumbled upon a naturally occurring material, called magnetite, by mistake. People were so astounded by it that tales were told of magical islands where magnetic nature was everywhere. The Chinese actually developed a compass around 4500 years ago using this magnetite! | ||
Despite not being the first people to study magnetism, Hans Christian Oersted did prove that electricity and magnetism were related by bringing a current carrying wire close to a compass needle. However, it wasn't until Maxwell published his findings in 1862 that led to the relationships between electricity and magnetism (Maxwell's Equations; see other Wikipedia page). | Despite not being the first people to study magnetism, Hans Christian Oersted did prove that electricity and magnetism were related by bringing a current carrying wire close to a compass needle. However, it wasn't until Maxwell published his findings in 1862 that led to the relationships between electricity and magnetism (Maxwell's Equations; see other Wikipedia page). | ||
Revision as of 13:40, 26 April 2016
claimed by Samah
A bar magnet creates a magnetic field, just like many other device (i.e. a current carrying wire), however, it has a different pattern of magnetic field which we will explore.
The Main Idea
The main idea for this topic is to explore how a bar magnet works and the effects that it has on its surroundings.
A Mathematical Model
In physics, it is important to keep track of your frame of reference. Treat an effect as if it is arising at the source location and ending at the observation location. The source location marks the beginning point for an effect. The result of the effect is gauged at the observation location.
Due to the fact that an observation location can either be on the axis of the magnet, or off the axis of the magnet, we have two different equations. Given a bar magnet with magnetic dipole moment μ, if the observation location is on the same axis as the magnet, assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles, we find that: [math]\displaystyle{ B = \frac{\mu _{0}}{4\pi }\cdot \frac{2\mu }{r^{3}} }[/math]
If the observation location is not on the axis of the bar magnet, and assuming that the distance from the observation location to the magnet is much greater than the separation distance of the two poles, we conclude that: [math]\displaystyle{ B = \frac{\mu _{0}}{4\pi }\cdot \frac{\mu }{r^{3}} }[/math]
A Computational Model

As you can see in this picture, the magnetic field of a bar magnet takes the exact same form as an electric field of a dipole. The magnetic lines flow out of the north pole of the magnet, and into the south pole of the magnet, in a curling fashion. However, the 'poles' are merely just conventions. They do not represent anything, and are terms assigned to each end, but it is true that the magnetic field will always flow out of the 'north' end. The Earth itself can also be represented by the computational model of a bar magnet; however, there are a few misconceptions about this. For starters, the magnetic North Pole is actually located near the geographic South Pole, and the magnetic South Pole is located near the geographic North Pole. Furthermore, the magnetic poles are off axis, meaning the are not directly at the top and bottom of the Earth. There is a difference of almost 1.5 degrees! It is also interesting to note that just because this illustration depicts the bar magnet as having two distinct ends, if you were to cut the magnet down the middle, it would polarize in such a way that you would end up with two bar magnets, not a single south pole and a single north pole.
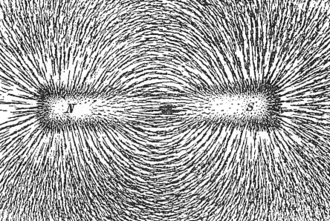
This picture depicts the magnetic field based on the dipoles of the magnet. The north end is the left side of the magnet and the south end is the right side of the magnet. The field follows the direction from the north side to the south side of the magnet.
Examples
Example 1: If a bar magnet is located at the origin with its North end aligned with the positive X-axis, what are the directions of the magnetic field at the following observation locations: above, below, to the left, to the right, and in a plane that is above the magnet?
We already know that the field of a bar magnet flows out of the north end and into the south end in a curling fashion. So, using the diagram above, it is easy to see that to the right of the magnet, the direction of the magnetic field points in the +X direction. At a position to the left of the magnet, the field is flowing back into the south end of the magnet, so the direction of the magnetic field at this location is also in the +X direction.
The field above and below the magnet is flowing from the right to the left at both locations, so the direction of the magnetic field above and below the magnet is in the -X direction.
At a different plane (z ≠ 0), there is no magnetic field, because we can assume that bar magnet acts as a 2-D dipole.
Example 2: A bar magnet with magnetic dipole moment 0.58 A∙m2 lies on the negative x axis, as shown in the figure below. A compass is located at the origin. Magnetic north is in the negative z direction. Between the bar magnet and the compass is a coil of wire of radius 3.5 cm, connected to batteries not shown. The distance from the center of the coil to the center of the compass is 9.6 cm. The distance from the center of the bar magnet to the center of the compass is 23.0 cm. A steady current of 0.96 A runs through the coil. Conventional current runs clockwise in the coil when viewed from the location of the compass. Despite the presence of the magnet and coil, the compass still points north.
(a) Which pole of the bar magnet is closer to the compass? (b) How many turns of wire are in the coil?
Part A: Because the conventional current runs clockwise in the coil, you can use right hand rule to determine what direction the magnetic field is due to the coil. This tells us that the magnetic field due to the coil is in the -X direction. In order for the compass to stay still, the magnet needs to directly oppose the magnetic field of the coil, meaning its magnetic field has to point in the +X direction, meaning the north pole would have to be nearer the compass.
Part B: Because the magnetic field created by the coil is equal to the magnetic field created by the magnet, we can set their two fields equal to each other: [math]\displaystyle{ \frac{\mu _{0}}{4 \pi } \cdot \frac{2\mu }{r^{3}} = \frac{\mu _{0}}{4 \pi } \cdot \frac{2NI\pi R^{2}}{(z^{2}+R^{2})^{3/2}} }[/math]
Rearranging to solve this equation for N, we get: [math]\displaystyle{ N = \frac{\mu (z^{2}+R^{2})^{3/2}}{I\pi R^{2} d^{3}} }[/math]
Plugging in .58 A∙m2 (the magnetic dipole moment, μ), .096 meters for z, .035 meters for R, .96 Amps for I, and .23 meters for d, we get that the number of loops in the coil is 14.
Connectedness

One very interesting applications of magnets is their ability to levitate objects. This is the main driving force in the case of MAGLEV trains. Magnetic levitation, or MAGLEV trains, hover above a long series of magnets where the magnets on the bottom of the train repel the magnets on the tracks below it. Sending an electric current through the coils on the bottom of the track allows the train to levitate a few inches off the ground, and propelling the current through the guided coils on the bottom of the track propels the train forward at unbelievable speeds (up to 250 MPH)!
Making the train levitate is a useful tool because it reduces the amount of friction between the wheels and the track, and it allows for less fossil fuels to be used in order to make the train propel forwards.
Magnetism is also used in medical technology. Medical Resonance Imaging (MRI) machines use magnetic fields and radio waves to create images of the body.
History

The first magnets were not invented, but rather discovered. The ancient Greeks and ancient Chinese stumbled upon a naturally occurring material, called magnetite, by mistake. People were so astounded by it that tales were told of magical islands where magnetic nature was everywhere. The Chinese actually developed a compass around 4500 years ago using this magnetite!
Despite not being the first people to study magnetism, Hans Christian Oersted did prove that electricity and magnetism were related by bringing a current carrying wire close to a compass needle. However, it wasn't until Maxwell published his findings in 1862 that led to the relationships between electricity and magnetism (Maxwell's Equations; see other Wikipedia page).
External links
- MAGLEV Trains: http://www.scienceclarified.com/everyday/Real-Life-Physics-Vol-3-Biology-Vol-1/Magnetism-Real-life-applications.html
- More information on Bar Magnets: http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/elemag.html
References
- http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/elemag.html
- https://en.wikipedia.org/wiki/Magnet#/media/File:VFPt_cylindrical_magnet_thumb.svg
- http://www.howmagnetswork.com/history.html
- https://en.wikipedia.org/wiki/Maglev#/media/File:Series_L0.JPG
- https://en.wikipedia.org/wiki/James_Clerk_Maxwell#/media/File:James_Clerk_Maxwell.png
Category: Fields
Created by: John Joyce