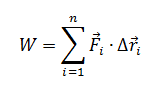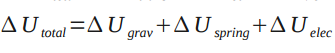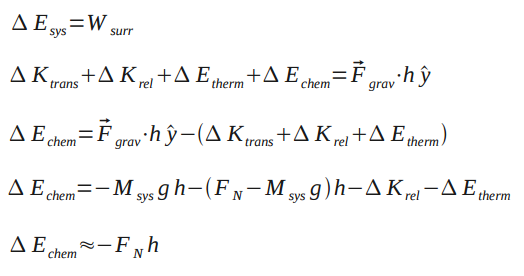Real Systems

This topic has been claimed by mwyatt6

The Main Idea

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

In Point Particle Systems, the only change in energy is from translational kinetic energy because every force is assumed to act on the center of mass. Up until Week 10, we have been measuring change in energy of systems using the Point Particle Method. From what we learned in Week 10 though, we know that translational kinetic energy is not the only type of energy there can be a change in (see: Thermal Energy and Translational, Rotational and Vibrational Energy). In a real system, you must consider the point of application of each force when calculating the change in energy. Also in real systems, forces may also occur over a different displacement than the displacement of the center of mass. These two key differences lead to an interesting mathematical model that differs from that used for the Point Particle Method.

A Mathematical Model

The mathematical equation used for Real Systems can vary depending on what his happening within and on the system. For the sake of flow with the WikiPhysicsBook, we will be analyzing real systems with the energy principle.

(We are ignoring Q for the sake of simplicity. It will not be taken into account in the subsequent examples despite the possible transfer of energy from temperature differences). E is the total energy of the system and W is the net work done from the surroundings on system. The major difference of a point particle system versus a real system is in the calculation of Work. In a point particle system, it is calculated by the net force dot product with the change in the position of the center of mass. However, Work in a real system is calculated by:

This means that the summation of the all the external forces dot product with the distance each force was applied amounts to the total change in energy of the real system. The change in the mathematical equation for Work between a point particle system and a real system is important because now different forms of energy may be taken into account. In a real system, the change in energy of a system can be given by:

Where, total change in internal energy (U) is given by:

total change in kinetic energy (K) is given by:

and change in Miscellaneous Energy is given by:

Examples

In order to better display the difference of Real Systems from Point Particle Systems, the examples done here will be the same examples done from Point Particle Systems.

Jumper Model

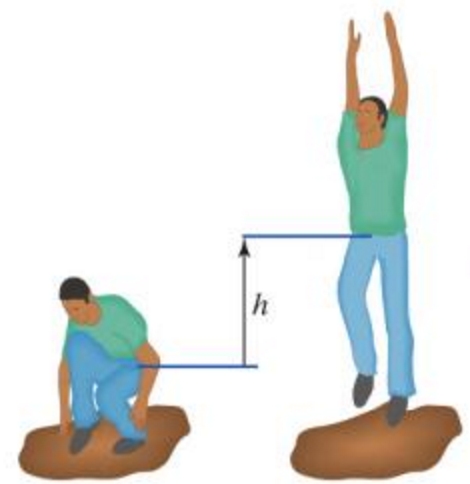Problem: You jump up so that your center of mass has moved a distance h. How much chemical energy did you expend?

From the Point Particle System analysis, we know that and .

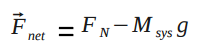
System: Person Surroundings: Earth+Floor

Initial State: Crouched down

Final State: Extended and moving with speed v

Yo-Yo

link title(Chabay)

Step 1: Solve for Point Particle System

In this part of the problem, when it the point particle is the only thing in the system, the only thing that can be solved for is the translational kinetic energy. Since there is only one thing in the system, there is no potential energy involved and the only thing the particle can do it move or translate. The forces acting on the point particle are equal in magnitude and direction to the real system. However, their is one key difference discussed in the next section (Chabay)

Step Two: Solve for Real System

As stated before, the forces acting on the point particle are equal in magnitude and direction to the real system. However, the is one key difference is the displacement of the applied force.(Chabay)

Connectedness

How is this topic connected to something that you are interested in?

1. This topic interest me because from one single particle you can mathematically determine the other form of energy that can occur in various physical interaction. In addition, being able to take a large complex interactions whether springs, gravitational potential or rotational energies are involved, you can solve and break down the interactions

How is it connected to your major?

1. This topic is not directly connected to my major, but the underlying ideas connect very closely to my major. By first looking at a point particle we have a starting point to looking and breaking down a complex system. As a biochemist there are large complex biological systems that I will encounter in my studies.

While I may not be able to break everything down to one single point, starting off with the simplest path way to understand and comprehend the largest and most complex systems is a similar method to my topic. Like with real and Point particle systems, you start off with a simple point so that one part of the interaction can be understood, from there the rest of the system can be dissected and other interactions can be solved for. With biochemical system, understanding one path, than moving from their to larger paths will help you understand the whole system.

Is there an interesting industrial application?

1. I do not really know if their is a physical industrial application that can be seen from looking at real and Point particle systems. However, the methodology and thought process behind looking at a real system can be applied to many problem solving situations.

External links

[1]

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Wiki Commons Picture

--Nfortingo3(talk) 19:26, 28 November 2015 (EST)