Iterative Prediction: Difference between revisions
| Line 134: | Line 134: | ||
==References== | ==References== | ||
CHANGE LECTURE SLIDES | |||
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. '''Wednesday, Week 2 Lecture Slides. Fenton, Flavio H''' | |||
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall | Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. '''Monday, Week 3 Lecture Slides. Fenton, Flavio H''' | ||
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall | Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. Lab 07 Fancart Energy & Spring-Mass Instructions, Greco, Edwin | ||
Revision as of 23:37, 25 November 2016
JENNIFER YU (FALL 2016)
What is Iterative Prediction?
Iterative Prediction - a process used to predict the effects of a force (constant or varying), on the motion of an object over a specific time interval that is split up into many smaller intervals.
During each time interval (∆t):
• The force acting on the object is found
• Using the net force (Fnet), calculate the change of momentum (∆p) of the object
• Using Fnet and ∆p, calculate the change in position of the object
Mathematical Explanation
• Fnet = "some number"
• ∆p = Fnet*∆t
• ∆r = (v)*∆t
NOTE: The velocity used in the position update equation is the new velocity! Always use the velocity calculated from the final momentum in the previous step. [(p final /m object) = v]
Why do we use Iterative Prediction?
Iterative Prediction is a necessary technique to employ when doing physics because, even though our fundamental principles are based on calculus and derivatives and you should be able to solve these problems using integrals, it is often impossible to solve the integrals required to solve complex problems. Iterative Prediction also becomes much more convenient when you implement it using a program, such as vPython, which allows you to make the approximation use as many steps as your processing power can handle, which can make your prediction much more accurate.
A Mathematical Model
By starting from the general equation for the Momentum Principle, a formula can derived to predict the momentum of a given system at a specified point in the future. This is often referred to as the momentum update form of the Momentum Principle:
(1) [math]\displaystyle{ {\frac{∆\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math]
A system's change in momentum is equal to the net force acting on it over a specific interval of time.
(2) [math]\displaystyle{ {\vec{p}_{f} - \vec{p}_{i} = \vec{F}_{net}{Δt}} }[/math]
∆ stands for final minus initial. In this case, it's the system's final momentum minus its initial momentum that results in the overall change in momentum of the system.
(3) [math]\displaystyle{ {\vec{p}_{f} = \vec{p}_{i} + \vec{F}_{net}{Δt}} }[/math]
By adding the initial momentum value to the other side of the equation, it is now possible to solve for value of the system's final momentum.
Generally, the third form of the momentum principle is the most commonly used form in updating the momentum of a system. Due to the nature of iterative prediction (over many small intervals), any aspect of the equation can be "non-uniform" and still give calculable results.
To find the velocity used in the Position Update Formula, use the "final momentum" from the Momentum Update Equation to solve for the final velocity.
[math]\displaystyle{ {\frac{\vec{p}_{f}}m = \vec{v_{avg}}} }[/math]
Position Update Formula: [math]\displaystyle{ {\vec{r}_{f} = \vec{r}_{i} + \vec{v}_{avg}{Δt}} }[/math]
A Visual Model
As the momentum update formula suggests, the final momentum (shown here as [math]\displaystyle{ \vec{p}_{future} }[/math]) of a system after a given change in time should be the vector sum of the initial momentum (denoted [math]\displaystyle{ \vec{p}_{now} }[/math]) and the net force on the system multiplied by the scalar time change ([math]\displaystyle{ \vec{F}_{net}{Δt} }[/math]).
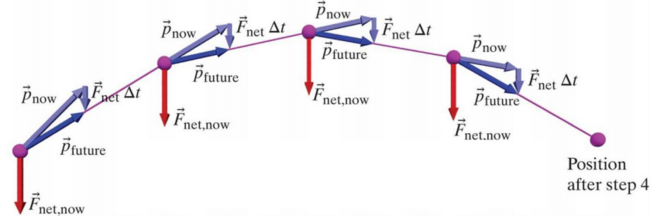
As the diagram suggests, each individual step can be analyzed through application of the momentum update form of the Momentum Principle. Once the final momentum is calculated, by utilizing the position and velocity update formula, the final velocity and position of the system can be determined at the end of the time interval of interest.
You can observe this Iterative Prediction in action by viewing this Vpython Script[1] (http://www.glowscript.org/#/user/JBarua/folder/Public/program/ProjectilePublic). It shows the flight path of a ball given an initial positive x and y velocity until it hits the ground, calculated using Iterative Prediction. In order to get a visual cue on how changing the time step of an Iterative Prediction calculation, try changing the deltat value from .15 to .05. You will see that making deltat smaller will place the approximation points closer together, which will give the ball's flight path a more consistent curve.
Example Calculations
There are a variety of different problems that can be solved by utilizing the momentum update form of the Momentum Principle. They can vary in difficulty and require any number of iterations. It is often prudent to calculate these iterations in a program loop to save time and avoid miscalculations.
Example #1 - Momentum Update
A boy standing on level ground throws a 2 kg ball into the air at an initial velocity of [math]\displaystyle{ {\lt 8,6,0\gt m/s} }[/math]. If the only force acting on the ball is gravity, what is the final momentum of the ball after 0.2 seconds?
This problem can be solved simply by solving for final momentum in the momentum update equation:
Example #2 - Trajectory Maxima
A 1 kg ball is kicked from location [math]\displaystyle{ {\lt 9,0,0\gt m} }[/math] giving it an initial velocity of [math]\displaystyle{ {\lt -10,13,0\gt m/s} }[/math]. What is the maximum height that the ball will reach along its trajectory?
This problem is a bit more complicated than the previous one. Before calculating the maximum height of the ball, we must know the time it takes for the ball to reach its maximum height by analyzing the motion of the ball in the +y direction through the momentum update equation:
Now that we know how long it takes for the ball to reach its maximum height, we can solve for the final height of the ball by utilizing the position update equation:
Example #3 - Varying Force
Model the motion of a spring with a ball attached to the end, taken into consideration of two forces, gravity (constant) and spring force (non-constant)
This is a good example of a problem that can most easily be solved using a computer program and knowledge of Iterative Prediction. In order to iteratively update the position of the ball and spring, three steps need to be taken inside of our while loop.
Step 1: Calculate net force Calculating the net force requires you first to calculate both the spring force vector and gravitational force vector based on the current position of the ball, then add them to get a net force vector.
Step 2: Apply Momentum Principle Now that we know our net force vector, we need to use the Momentum Principle to find the change in momentum when that force is applied for our time step.
Step 3: Update Position Finally, now that we know the change in momentum(and in turn the change in velocity), we can use our position update formula to update the position of both the ball and the axis of the spring. Don't forget to update your time!
Connectedness
Iterative Prediction serves as a basis for modeling complex motion throughout time. While some of the basic examples do not appear to be too trivial, iterative prediction can be used to solve more difficult problems. Having now almost completed a semester of mechanics, one topic that I became interested in almost right away was this idea of being able to solve problems in which we aren't necessarily concerned with the physics of the system at the current moment in time. Iterative Prediction of motion is just one of the many different techniques we have used to study the "physics of the future."
Iterative Prediction can have many applications to the field of Chemical Engineering, namely in the principles governing momentum transfer in chemical processes. A simple example is in studying fluid flow in a process. By making use of iterative prediction and the momentum principle, a chemical engineer can model the change in momentum of the fluid flow by analyzing the net force on the fluid (likely due to pressure) and the initial momentum of the fluid flow. In industry, this can be important so as to predict accumulation in a process and thus allow for modeling of an efficient process to maximize output.
History
The physics behind iterative prediction is nothing more than simple application of the momentum principle and projectile motion, which has existed in classical mechanics for quite some time. However, the practical application of iterative prediction for analyzing systems has evolved due to advances in computational methods and technology. With the computational power of a computer to iteratively calculate changes in momentum through time, one can analyze a system's motion extremely quickly without tedious and difficult mathematical calculations.
See also
There are many public resources that delve further into iterative prediction examples of more complex motion.
External links
MIT Open Courseware Introductory Mechanics
Iterative Prediction with VPython
References
CHANGE LECTURE SLIDES Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. Wednesday, Week 2 Lecture Slides. Fenton, Flavio H
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. Monday, Week 3 Lecture Slides. Fenton, Flavio H
Georgia Institute of Technology. Physics Department. PHYS 2211. Fall 2016. Lab 07 Fancart Energy & Spring-Mass Instructions, Greco, Edwin


