Inclined Plane: Difference between revisions
| Line 50: | Line 50: | ||
if the inclined plane has a friction<br> | if the inclined plane has a friction<br> | ||
:<math>\mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \,</math> (in this case, <math>\phi = \tan^{-1} \mu \,</math>)<br> | :<math>\mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \,</math> (in this case, <math>\phi = \tan^{-1} \mu \,</math>)<br> | ||
<math>\theta < \phi\,</math>: Downhill applied force is needed.<br> | :<math>\theta < \phi\,</math>: Downhill applied force is needed.<br> | ||
<math>\theta = \phi\,</math>: Infinite mechanical advantage.<br> | :<math>\theta = \phi\,</math>: Infinite mechanical advantage.<br> | ||
<math>\theta > \phi\,</math>: The mechanical advantage is positive. Uphill force is needed.<br> | :<math>\theta > \phi\,</math>: The mechanical advantage is positive. Uphill force is needed.<br> | ||
==See Also== | ==See Also== | ||
Revision as of 01:31, 27 November 2016
Claimed by Sunmin Kim Skim883 (Fall2016)
Definition
inclined(adj): deviating in direction from the horizontal or vertical; sloping
plane(n):a flat or level surface
Inclined plane means a plane with a level surface. It is inclined at a angle to the horizontal.
Why do we need to know?
When we solve physics problems, it is necessary to understand free diagram.
Understanding this inclined plane will help you apply gravity and angles on calculating forces.
History
Our ancestors have used inclined plane since prehistoric times to move heavy objects.
The most famous artifact that is believed to be constructed using inclined plane is Stonehenge, Pyramids.


Inclined Plane was treated as a simple machine till Renaissance.
Leonardo Da Vinci found out the first elementary of sliding friction in inclined plane.
Uses
You may see this almost every day in your daily life. The inclined planes are needed for loading and unloading heavy goods on transportation such as ships, trucks and planes because it has mechanical advantage of reducing the forces required to move heavy goods.

Diagram of the Inclined Plane
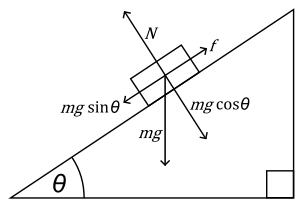
θ= Angle of the plane to the horizontal
g= Acceleration due to gravity
m= Mass of object
N= Normal force (perpendicular to the plane)
f = frictional force of the inclined plane (sometimes it is omitted on test problems)
mgSinθ= A force parallel to the plane (mgSinθ > f the body slides down the plane)
mgCosθ= A force acting into the plane (opposite to N)
Terminology
Let's imagine there is a right triangle. The side opposite to the right angle is a Slant. The side on the bottom is Run The side vertical to the bottom is Rise
Slope: A slope brings a mechanical advantage to the incline plane.
- [math]\displaystyle{ \theta = \tan^{-1} \bigg( \frac {\text{Rise}}{\text{Run}} \bigg) \, }[/math]
Mechanical Advantage
Fw is a gravitational force that applies on the plane
Fi is a force exerted on the object and parallel to the plane
- [math]\displaystyle{ \mathrm{MA} = \frac{F_w}{F_i}. \, }[/math]
if the inclined plane is frictionless,
- [math]\displaystyle{ \text{MA} = \frac{F_w}{F_i} = \frac {1}{\sin \theta} \, }[/math] (in this case, [math]\displaystyle{ \sin \theta = \frac {\text{Rise}}{\text{Length}} \, }[/math])
if the inclined plane has a friction
- [math]\displaystyle{ \mathrm{MA} = \frac {F_w}{F_i} = \frac {\cos \phi} { \sin (\theta - \phi ) } \, }[/math] (in this case, [math]\displaystyle{ \phi = \tan^{-1} \mu \, }[/math])
- [math]\displaystyle{ \theta \lt \phi\, }[/math]: Downhill applied force is needed.
- [math]\displaystyle{ \theta = \phi\, }[/math]: Infinite mechanical advantage.
- [math]\displaystyle{ \theta \gt \phi\, }[/math]: The mechanical advantage is positive. Uphill force is needed.
See Also
Free Body Diagram
Normal Force
References
http://www.newworldencyclopedia.org/entry/Inclined_plane
http://www.dictionary.com