Perpetual Freefall (Orbit)

Currently Under Edit by Nicole Ihrie (Fall 2016)

The Main Idea

Perpetual free fall, or orbit, is when the force of gravity is equal to the centripetal force of the object’s motion in space. The centripetal force fluctuates based on changes in the object’s tangential velocity. The force of gravity pulls inward on the object, and the centripetal force pushes the object out. When these perpendicular forces are equal, the object will follow a circular path around the massive body which is the source of gravity. The object is in perpetual free fall because gravity is the only force acting upon it, but the velocity continuously prevents the object from just falling towards the earth. This perpetual free fall causes a feeling of weightlessness for the object. In order to enter the state of orbit, the particular conditions described above must be met. The pictures on the right demonstrate this concept. If the tangential velocity is too high, then the object will reach an escape velocity and will continue to travel outward away from the massive object. If the tangential velocity is too low, then the object will fall towards the massive object. For organizations such as NASA or Boeing that utilize satellites, gravity must be overcome to exit the lower atmospheres and make sure their technologies maintain orbit and do not fall back to Earth. This is achieved via perpendicular propulsion and altitude adjustment in lower atmospheres where air resistance in present, or happens when there is a high enough stable velocity outside the Earth's atmosphere.

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Initial Projectile Motion of Object

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Object Falling Around Earth

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Centripetal force greater than gravitational

A Mathematical Model

Calculating an objects motion is based around the Newton’s law of universal gravitation and the momentum principle which is described by the equation [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{object} = \vec{F}_{net} }[/math], where [math]\displaystyle{ \vec{F}_{net} }[/math] is equal to the change in the momentum of the object. Gravity is the only force acting on an object which has begun perpetual freefall outside the atmosphere. The gravitational force equation for an object near the surface of the Earth is [math]\displaystyle{ \vec{F}_{gravity}= \lt 0,{mass}_{object}*{a}_{gravity},0\gt }[/math], where a is acceleration due to gravity: -9.8 m/s. Perpetual freefall, however, follows Newton’s law of universal gravitation which is dependent on the mass of both objects, and their distance apart. [math]\displaystyle{ {F}_{gravity} = G \frac{m_1*m_2}{r^2}\ }[/math] where G is the universal gravitation constant: 6.7e-11, r is the distance between the two objects, and m1 and m2 are the masses of both objects respectively.

Because gravity is the only force acting on the object once it is free from Earth's atmosphere, [math]\displaystyle{ {Force}_{gravity} }[/math] is equal to the objects net force. Once net force is calculated, the momentum principle equation is manipulated so that the object's momentum can be updated as a function of the net force acting on the object. The equation [math]\displaystyle{ {\vec{p}_{object_{final}} } = \vec{p}_{object_{initial}}+ \vec{F}_{net}*{\Delta}{t} }[/math] is used where p is the objects momentum and [math]\displaystyle{ \Delta }[/math]t is the change in time between measurements or data points. Once change in momentum is calculated, the velocity of the object can be found using the assumption that [math]\displaystyle{ \vec{velocity}_{average} = \frac{\vec{p}_{object_{final}}}{{mass}_{object}} }[/math]. This velocity value is then used to update the objects position using [math]\displaystyle{ {\vec{r}_{object_{final}} } = \vec{r}_{object_{initial}}+ \vec{velocity}_{average}*{\Delta}{t} }[/math] where r is the object's position.

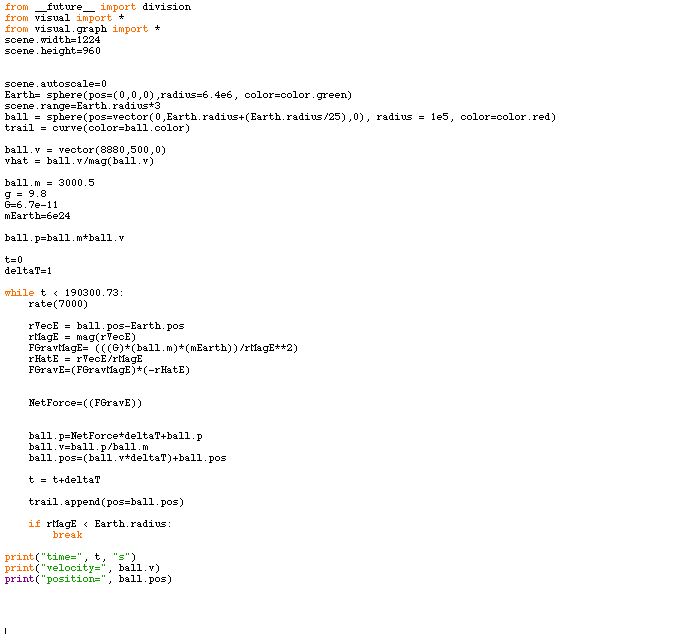
A Computational Model

Below is the computational code written in vPython language. The code consists of a setup of the scene, initial conditions and constants, calculation of force, and an update of momentum, velocity and position. All of these components are expressed visually as a simulation.

Examples

Simple

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Connectedness

Perpetual freefall (orbit) from a frame of reference that it's possible for an object to fall past the curvature of the Earth comparative to an object merely orbiting around the Earth as a constant velocity is an interesting concept that gives a more accurate representation of how objects actually orbit the Earth. The industrial applications of this principle are seen everyday, as companies such as [Boeing], [NASA], and [SpaceX] must use the most basic form of these principles and expand upon it to achieve space and outer atmospheric flight.

History

The planetary orbits had been observed by astronomers for decades before the first theories on planetary motion were concieved. [| Johannes Kepler] was one of the first to observe and prove that the motions that were being observed were elliptical in nature. From this, [Sir Isaac Newton] was able to combine Kepler's principles with his own theories of motion and that Keplar's theories could be proven by his own theory of gravitation. This derivation led to the relation of a planet's mass to the gravitational force acting on an object which became Newton's gravitational equation used in the calculation of orbits.

See also

[| Law of Gravitation] [| Newton's Laws] [| Momentum Principle] [| Projectile Motion]

Further reading

[| The Observer's Guide to Planetary Motion]