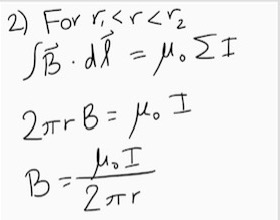Ampere's Law

Improved by Isabella Caballero Spring 2017

Ampere's Law, the fourth of Maxwell's equations, is a relationship between the magnetic field of a closed path and the current within the path. Discovered by Andre-Marie Ampere, this law is particularly useful when calculating the current distributions with considerable symmetry.

The Main Idea

A student is usually first taught how to find the magnetic field caused by the flow of individual charges and/ or currents. Ampere's law allows us to see a magnetic field and determine the currents that generate this field. Ampere’s law is a quantitative relationship between measurements of magnetic field a long a closed path and the amount and direction of the currents passing through that boundary. Ampere’s law is a quantitative relationship between measurements of magnetic field a long a closed path and the amount and direction of the currents passing through that boundary.

Here is a summary of the key steps in applying Ampere’s law:

According to the Massachusetts Institute of Technology, Ampere's law can be broken down into seven individual steps:

Step 1: "Identify the 'symmetry' properties of the charge distribution." What can this tell you about the big picture?

Step 2: "Determine the direction of the magnetic field." How does this affect the sign of your answer?

Step 3: "Decide how many different spatial regions the current distribution determines."

Step 4. "Choose an Amperian loop along each part of which the magnetic field is either constant or zero." How can you know when each case occurs?

Step 5: For each region of space, "Calculate the current through the Amperian Loop."

Step 6: For each region of space, calculate the line integral of the magnetic field and the change in area around the closed loop.

Step 7: For each region of space, equate that integral with mu(I)enc and solve for the magnetic field.

A Mathematical Model

[math]\displaystyle{ \oint_C \mathbf{B} \cdot \mathrm{d}\boldsymbol{\ell} = \mu_0 \iint_S \mathbf{J} \cdot \mathrm{d}\mathbf{S} = \mu_0I_\mathrm{enc} }[/math]

A Computational Model

To view using Ampere's law to calculate the magnetic field of a toroid: https://www.youtube.com/watch?v=jdsUQs9w0uw

For the magnetic field in a coaxil cable from Ampere's Law: https://www.youtube.com/watch?v=IMoN6MVgOgA

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

1. Calculate the magnetic field of a solenoid with N number of turns at a point in the center of the solenoid.

1. Choose a path that has nonzero current intersecting it and includes the point at which the magnetic field is being calculated.

Let our path be the dotted rectangle with width (length parallel to solenoid) L.

2. Walk along the path counterclockwise, starting from the top-right corner of the rectangle.

3. Add up the individual contributions of each leg of the path. From the top right corner to the top left corner, the contribution is 0, since the magnetic field outside the solenoid is very small, we approximate it to be zero. From the top left corner to the bottom left corner, the contribution is again 0 since the path and the magnetic field are perpendicular to each other. Therefore, their dot product is 0. From the bottom left corner to the bottom right corner, the contribution is BL. From the bottom right corner to the top right corner, again the contribution is 0, because, again, the path and the magnetic field are perpendicular to each other.

4. Set the sum of contributions equal to [math]\displaystyle{ \mu_0 \Sigma I }[/math] Since this solenoid has N turns, we must multiply the current I by N.

[math]\displaystyle{ BL = \mu_0 NI }[/math]

[math]\displaystyle{ B = {{\mu_0 NI}\over L} }[/math]

2. Calculate the magnetic field of a toroid with N number of loops inside the toroid.

1. We pick our path to travel along the perimeter of the toroid, letting the path be a circle of radius r, which is between the inner and outer radii of the toroid.

2. The contribution is simply the product of B and the circumference of our imaginary circle (our path):

[math]\displaystyle{ B2 \pi r = \mu_0 N I }[/math]

[math]\displaystyle{ B = {{\mu_0 N I}\over {2 \pi r}} }[/math]

Difficult

The cross section of a coaxial wire is shown below. The wire is the inner blue region and the shell is the outer blue region. Both wire and shell have a current of identical magnitude I, but the currents run in opposite directions. Both wire and shell have uniform current density.

Calculate the magnetic field at three different regions:

1) Inner blue region 2) White ring 3) Outer blue region

1)

2)

3)

4)

Connectedness

1. How is this topic connected to something that you are interested in?

An application of Ampere's law in an area that interests me is Maglev trains. It's fascinating how magnetic fields are strong enough to suspend the huge body that is a train. These trains do not use the same motors that are in regular trains. Instead they use electromagnets and guide the trains over a guideway, raising it approximately 0.39 and 3.93 inches. Because they float on air, this eliminates friction and allows the trains to reach speeds getter than 300 miles per hour. Damn. This excerpt from How Stuff Works indicates more about how they work- "Once the train is levitated, power is supplied to the coils within the guideway walls to create a unique system of magnetic fields that pull and push the train along the guideway. The electric current supplied to the coils in the guideway walls is constantly alternating to change the polarity of the magnetized coils. This change in polarity causes the magnetic field in front of the train to pull the vehicle forward, while the magnetic field behind the train adds more forward thrust."

1. How is it connected to your major?

Alternatively are the applications of Ampere's law in Industrial Engineering. As an Industrial Engineer, I experience a lot of opportunities for involvement in healthcare. Ampere's law is used for magnetic resonance imaging while using an MRI. Healthcare is always needed, and an important opportunity to impact the lives of other people in your community. http://www1.coe.neu.edu/~benneyan/healthcare/IE_at_Premier.pdf

1. Is there an interesting industrial application? cite http://www.gizmag.com/ge-magnetocaloric-refrigerator/30835/

An interesting industrial application that I've seen is also in the field of HVAC and involves refrigeration. And no it's not just the magnetism that lets you stick stuff on your fridge... The modern day fridge even though it's come a long way in terms of energy efficiency, still remains as the biggest leach of electricity in a household. Incorporating magnetism actually can have the effect of making refrigerators up to 30% more efficient than what's currently out there. It all started when the magnetocaloric effect, https://en.wikipedia.org/wiki/Magnetic_refrigeration when certain materials change temperatures in the presence of a varying magnetic field, was first observed. Such technology has not yet been implemented because of issues in how bulky it is. Michael Benedict, design engineer at GE Appliances describes it as being "about the size of a cart." That being said, be on the lookout in 10 or so more years when refrigerators based on this effect hit the markets!

Link to youtube video to embed: https://www.youtube.com/watch?v=WlKKKMTA7XM

Additionally, NASA utilizes the implications of Ampere's law when measuring the magnetic fields produced by time-varying currents when performing calculations on electric space thrusters and accelerators.

History

André-Marie Ampère, the founder of classical electromagnetism, was a French mathematician and physicist born into a merchant family. Due to his father’s strong beliefs, André was self-educated in his huge library. Fast forward about 30 years and André had become a well-established professor of mathematics, philosophy and astronomy at the University of Paris. In 1820, André had established what was later known as Ampere’s law. He was able to demonstrate that two parallel wires can be oriented, with different current flows, in a manner that let them either attract or repel one another. Andre established a relationship between the length of a current carrying wire and the strength of their currents. In 1827-28, André was elected as a Foreign Member of the Royal Swedish Academy of Science and a foreign member of the Royal Swedish Academy of Science. In 1881, a while after his death in 1836, the ampere, a standard unit of electrical measurement, was named after him.

When only a teenager, Andre's father was guillotined during the French Revolution before Ampere became a mathematics professor. However, it is admirable he still laid out the base of electrodynamics with his research and is considered one of the top researchers in experimental physics during his time.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Related topics or categories regarding Ampere's law, it would likely be helpful to understand all of Maxwell's equations: Gauss' law for electricity, Gauss' law for magnetism, Faraday's law of induction, in addition to Ampere's law. It is important to differentiate each formula and determine what it means and what it's looking for.

Further reading

Books, Articles or other print media on this topic

Maxwell's Equations, Paul G. Huray

Fundamentals of Electromagnetism: Vacuum Electrodynamics, Media, and Relativity, Arturo Lopez Davalos and Damian Zanette

External links

Internet resources on this topic

An incredible 3D representation of Electromagnetism and Maxwell's Laws: https://www.youtube.com/watch?v=9Tm2c6NJH4Y

References

This section contains the the references you used while writing this page

Section 22.6 PATTERNS OF MAGNETIC FIELD: AMPERE'S LAW pg. 914- 920

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/amplaw.html#c1

http://teacher.pas.rochester.edu/phy122/Lecture_Notes/Chapter31/chapter31.html

https://web.iit.edu/sites/web/files/departments/academic-affairs/academic-resource-center/pdfs/Amperes_law.pdf

http://www.maxwells-equations.com/ampere/amperes-law.php

http://spp.astro.umd.edu/SpaceWebProj/CLASSES%20PAGES/SupplnSummaries/Sum%202.pdf

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/amplaw.html

https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140005775.pdf http://www1.coe.neu.edu/~benneyan/healthcare/IE_at_Premier.pdf

https://www.teachengineering.org/lessons/view/van_mri_lesson_7

http://www.edisontechcenter.org/InductionConcept.html