Sign of a Potential Difference

CLAIMED BY DYLAN AMADOR (FALL '16)

---

Introduction

Recall from previous sections that the change in potential energy is equal to the charge times the change in potential difference. From Conservation of Energy, we know that an increase in potential energy is related to a decrease in kinetic energy, and vice versa. Furthermore, recall that the change in potential energy, potential difference, kinetic energy, etc. can be positive or negative.

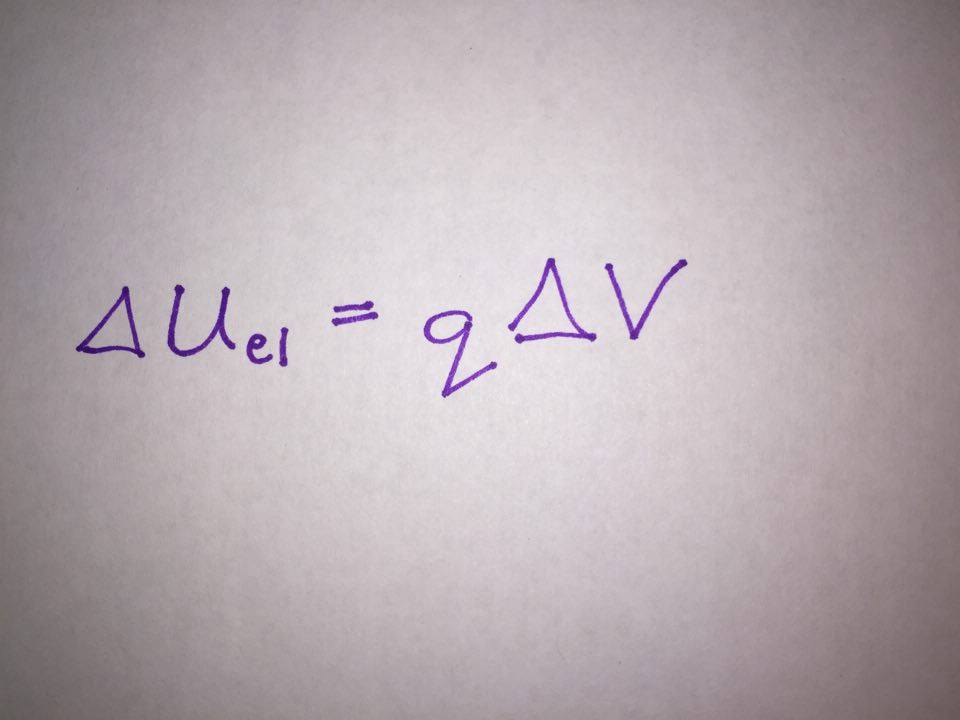
Direction of Path vs. Direction of Electric Field

From the equation relating potential difference with electric field and motion, we can see that the sign of the potential difference is dependent on the direction of both the electric field and displacement vectors. 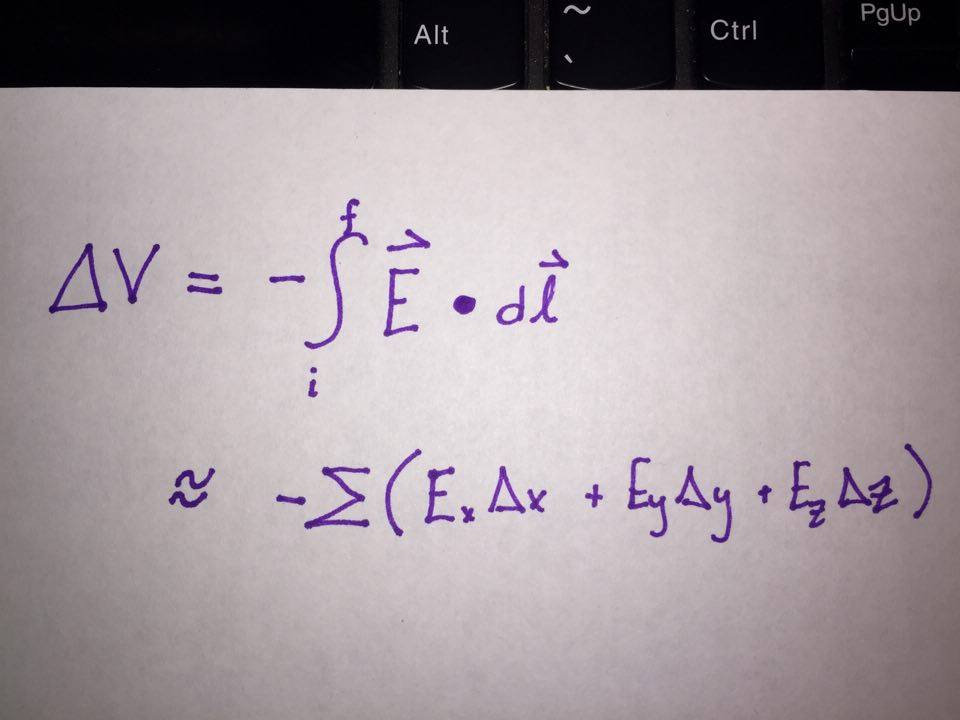For this equation, note that the result of the cross product between the electric field and displacement is negated before finding the potential difference. Furthermore, it is important to note that the electric field and displacement vectors are multiplied by the dot product. Because of this dot product, we will analyze 3 different scenarios: path in the direction of the electric field, path in the opposite direction of the electric field, and the path moving perpendicular to the direction of the electric field.

(1) Same Direction In this scenario, the dot product yields a positive result, so when multiplied by the negative term in the equation, the resulting potential difference will be negative.

(2) Opposite Direction When the electric field and displacement are in opposite directions, the result of the dot product will be negative which leads to a positive potential difference after multiplying that result by -1.

(3) Directions are Perpendicular For this scenario it will be critical to have a strong understanding of the dot product and how to calculate it. Remember that a dot product multiplies terms that are in the same direction before being summed for a total. This means that when finding the dot product of two perpendicular vectors, the result will be zero. To better understand this, imagine the electric field between two very long capacitor plates. The electric field points from one plate to the other, let's say in the +x direction. If you wanted to move a charge at any location between the plates in either the +y or -y direction, your displacement vector would point in one of these directions. Whether you moved the particle +y or -y direction, the dot product of the electric field and displacement will be zero. Moving forward with the concept of potential difference, this concept will be useful to remember for solving problems.

Indicating Path Direction (sign convention)

Consistent with previous convention, the delta symbol indicates "final - initial." We will use this same notation in showing the direction of the path. For example: Vb - Va ---> signifies the potential difference between location B (final) and location A (initial).

Examples

File:PotExamples.jpg

Summary

When determining the sign of