Motional Emf

Claimed by Jessica Pan(Fall 2016)

Motional emf is emf caused by motion in a magnetic field, leading to polarization. This is in contrast to how emf is generated in nature, namely through fluctuation of a magnetic field through a surface. Motional emf is difficult to observe visually using batteries, light bulbs, and compasses because it is so small.

The Main Idea

A metal bar moving in a magnetic field will create a magnetic force, which acts on the bar. The magnetic force makes the metal bar polarize. The polarized metal bar resembles and acts like a battery(the polarized bar's charges are separated, like a battery), which means that we can put the polarized bar in a circuit and then use it to generate a current in the circuit.

Additionally, when the metal bar is polarized, because of the charge separation, an electric force is created in the bar.

Polarization and Steady State

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

A conducting bar moving with velocity v is polarized as a result of the upwards magnetic force; see section 1.3 for a right-hand rule applicable to the scenario

Polarization occurs due to the shift of the mobile electron sea in one direction. Eventually, the shifting will stop; enough electrons will shift in a particular direction so that the electric force, in the opposite direction, balances out the magnetic force ([math]\displaystyle{ qvB=qE }[/math]). Consequently, in the steady state, [math]\displaystyle{ E=vB }[/math] and there is no net force on the bar, so the bar does not require any additional force to keep it moving at a constant velocity.

In the steady state, a nonzero E-field exists inside the metal bar; however, if the bar is not connected in a circuit, there is no current. This is because the electric force is balanced with the magnetic force, resulting in zero net force on the mobile electrons. The potential difference across the metal bar is then the product of the electric field and the length of the bar.

Driving Current

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

A circuit formed with a moving conducting bar on conducting, frictionless rails connected by a resistor

If the metal bar is used to form a circuit, where the bar is slid along on two frictionless metal rails that are also connected, then the charge separation in the bar mimics a battery and can drive a current.

When the bar, in the described configuration, has a force applied to it and initially begins to move from rest, the entire lattice of positive ions is pulled in the direction of the bar's velocity. The mobile electrons are left behind for a brief moment, causing a near-instantaneous polarization in the bar, but are then pulled along with the positive ions due to the electric interaction between the charges.

Now that the bar, moving within the magnetic field, has a velocity, the direction of the magnetic force can be determined through the right-hand rule. The mobile electrons will be affected by both this magnetic force and the force being applied on the bar. Eventually, over time, the net force on the bar decreases to zero, and the bar moves at a constant speed, with a balance between the force pulling the bar and the component of magnetic force on the mobile electrons in the opposite direction. A current now runs through the bar. The mobile electrons in the bar move toward the negatively charged end, rather than the positively charged end, because the continuous depletion of charge means that the electric field is always slightly less than what is needed to balance out the opposing magnetic field. Therefore, the electrons move to the negative end to maintain charge separation and the electric field.

The potential difference across the bar is still the product of the electric field and the length of the bar. If the bar does have some resistance, then it is treated like a battery with internal resistance. In the circuit, the potential difference round-trip is zero.

A Mathematical Model

A right-hand rule determining the directions of magnetic force, conventional current, and magnetic field

The potential difference across the metal bar is [math]\displaystyle{ \Delta V=emf=EL=v_{bar}BL }[/math]. If the bar has resistance, then [math]\displaystyle{ \Delta V=emf-r_{int}I }[/math].

When the bar in the circuit, in steady state, moves a distance [math]\displaystyle{ \Delta x }[/math] over a time [math]\displaystyle{ \Delta t }[/math], the work done is [math]\displaystyle{ F \Delta x }[/math] and the power supplied is [math]\displaystyle{ {F \Delta x}/{\Delta t} }[/math], or [math]\displaystyle{ Fv_{bar} }[/math]. If the rails in the circuit are connected by a resistor, then the power dissipated in the resistor is [math]\displaystyle{ ILBv_{bar}=I*emf={emf/R}*emf={emf^{2}}/R=RI^{2} }[/math].

Motional emf can be calculated in terms of magnetic flux: [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math].

A Computational Model

A simulation of motional emf can be found here.

Equations to remember

1. [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math].
2. During steady state, the electric force balances with the magnetic force([math]\displaystyle{ qvB=qE }[/math]), so [math]\displaystyle{ E=vB }[/math].

3.We know [math]\displaystyle{ \Delta V=emf }[/math], [math]\displaystyle{ \Delta V=EL }[/math], and [math]\displaystyle{ E=vB }[/math], so [math]\displaystyle{ \Delta V=v_{bar}BL }[/math].

4. Power is [math]\displaystyle{ P=I\Delta V }[/math].

Examples

Simple

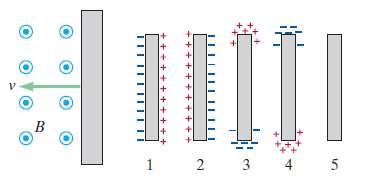
Taken from the Matter & Interactions textbook, variation of P60.

A neutral iron bar is dragged to the left at speed v through a region with a magnetic field B that points out of the page, as shown above. (a) In which direction is the magnetic force? (b) Which diagram (1–5) best shows the state of the bar?

(a) The magnetic force points upwards. Use the right hand rule.
(b) Diagram 3 shows the correct polarization based on the direction of the magnetic force.

Middling

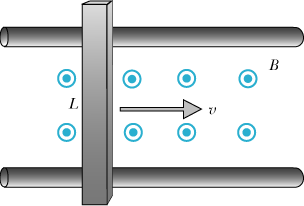
Taken from the Matter & Interactions textbook, variation of P63.

A neutral metal rod of length 0.21 m slides horizontally at a constant speed of 7 m/s on frictionless insulating rails through a region of uniform magnetic field of magnitude 0.18 tesla, directed out of the page as shown in the diagram. (a) Is the top of the moving rod positive or negative? (b) After the initial transient, what is the magnitude of the net force on a mobile electron inside the rod? (c) What is the magnitude of the electric force on a mobile electron inside the rod? (d) What is the magnitude of the magnetic force on a mobile electron inside the rod? (e) What is the magnitude of the potential difference across the rod? (f) In what direction must you exert a force to keep the rod moving at constant speed?

(a) The top of the moving rod is negative. Use the right-hand rule.
(b) [math]\displaystyle{ \left | \overrightarrow{F}_{net} \right |=0 \: N }[/math] because after the initial transient the system is in steady state and the electric force balances out the magnetic force.
(c) First we recognize that the system is in steady state, so [math]\displaystyle{ E=vB=7 \times 0.18=1.26 }[/math]. Then [math]\displaystyle{ \left | \overrightarrow{F}_{E} \right |=\left | qE \right |=\left | -1.6 \times 10^{-19}(1.26) \right |=2.016 \times 10^{-19} \: N }[/math].
(d) In steady state, [math]\displaystyle{ \left | \overrightarrow{F}_{E} \right |=\left | \overrightarrow{F}_{B} \right | }[/math]. So, [math]\displaystyle{ \left | \overrightarrow{F}_{B} \right |=2.016 \times 10^{-19} \: N }[/math].
(e) [math]\displaystyle{ \Delta V=EL=v_{bar}BL=7 \times 0.18 \times 0.21=0.2646 \: V }[/math].
(f) No force is needed. The system is in steady state, so no additional force needs to be applied to keep the rod at constant speed.

Difficult

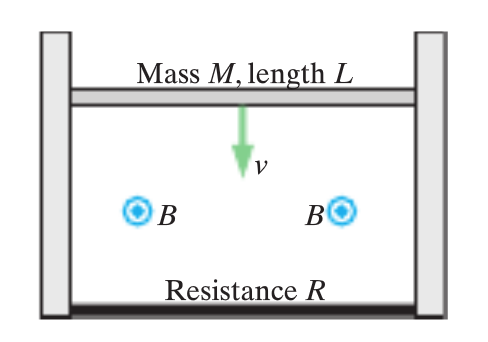
Taken from the Matter & Interactions textbook, P64.

A metal bar of mass M and length L slides with negligible friction but with good electrical contact down between two vertical metal posts, as shown above. The bar falls at a constant speed v. The falling bar and the vertical metal posts have negligible electrical resistance, but the bottom rod is a resistor with resistance R. Throughout the entire region there is a uniform magnetic field of magnitude B coming straight out of the page. (a) Calculate the amount of current I running through the resistor. (b) What is the direction of the conventional current I? (c) Calculate the constant speed v of the falling bar. (d) What is the direction of the electric force acting on a positive mobile charge? (e) What is the direction of the magnetic force acting on the bar?

(a) The bar is already falling at a constant velocity, so [math]\displaystyle{ \left | \overrightarrow {F}_{net} \right |=0 }[/math] and [math]\displaystyle{ E=vB }[/math]. We know that [math]\displaystyle{ I={emf}/R }[/math] and [math]\displaystyle{ {emf}=EL=vBL }[/math] so it follows that [math]\displaystyle{ I={vBL}/R }[/math].
(b) The magnetic force [math]\displaystyle{ qvB }[/math] causes positive charges to move left and negative charges to move right. Conventional current flows from the positively charged end of the bar to the negative end, so it runs counterclockwise.
(c) The conventional current I running through the bar causes a magnetic force upwards of magnitude [math]\displaystyle{ ILB\sin 90^{\circ}=({vBL}/R)LB={vL^{2}B^{2}}/R }[/math]. This magnitude must balance out the gravitational force [math]\displaystyle{ Mg }[/math] because the magnetic and gravitational forces must cancel for [math]\displaystyle{ \left | \overrightarrow {F}_{net} \right |=0 }[/math] and the bar to have a constant velocity v. So, setting the forces equal to each other, [math]\displaystyle{ v={MgR}/{L^{2}B^{2}} }[/math].

Note: We can also find the speed of the falling bar with [math]\displaystyle{ \left | emf \right |=\left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right | }[/math]. Using the loop rule, [math]\displaystyle{ 0=IR - {emf} }[/math]. So [math]\displaystyle{ \left | \frac{\mathrm{d} \Phi_ {mag}}{\mathrm{d} t} \right |=IR }[/math]. We can transform that to [math]\displaystyle{ IR=\frac{\mathrm{d} (BA)}{\mathrm{d} t} }[/math]. Since B is constant, [math]\displaystyle{ IR=B(\frac{\mathrm{d} (A)}{\mathrm{d} t}) }[/math]. We can transform that to [math]\displaystyle{ IR=B(\frac{\mathrm{d} (Lh)}{\mathrm{d} t}) }[/math], where h is the distance of the bar above the bottom rod. Since L is constant, [math]\displaystyle{ IR=BL(\frac{\mathrm{d} (h)}{\mathrm{d} t}) }[/math]. [math]\displaystyle{ \frac{\mathrm{d} (h)}{\mathrm{d} t}) }[/math] is the velocity of the bar, so [math]\displaystyle{ IR=BLv }[/math]. Solving for v, [math]\displaystyle{ v={MgR}/{L^{2}B^{2}} }[/math].
(d) The electric force acting on a positive mobile charge points towards the right in the bar. Using the right hand rule, with B pointing out of the page, v pointing downwards, we know that the magnetic force points to the right. This means that the bar is polarized with positive charges on the left side of the bar and negative charges on the right side. The electric force points from positive charges to negative charges, so the electric force points towards the right.
(e) The magnetic force acting on the bar points upwards. We know that current flows from left to right in the bar because positive charges are polarized on the left side of the bar and negative charges are on the right side of the bar. Using the right hand rule, with B pointing out of the page and current pointing to the right, we find that the magnetic force points upwards.

Connectedness

The concept of power generated from a mechanical input is how electric generators function. The mechanical energy is commonly supplied by falling water at dams or expanding steam in turbines.

History

Michael Faraday

The phenomenon of electromagnetic induction, the emf produced from the interactions between a magnetic field and an electric circuit, was discovered independently in 1831 by Michael Faraday and 1832 by Joseph Henry (Faraday published his results first). Many of Faraday's ideas were rejected by the scientists of the day because they had no mathematical basis, but James Clerk Maxwell used these ideas to formulate his electromagnetic theory and Maxwell's equations.

At the time, it was not well understood how Maxwell's equations related to moving charged objects. J.J. Thomson was the first to attempt to derive, from Maxwell's equations, an equation describing effects on moving charged particles, and Oliver Heaviside built upon this work and fixed errors in Thomson's derivation. In 1892, Hendrik Lorentz finally derived the correct equation called the Lorentz force. The magnetic force component of the Lorentz force describes motional emf, as the magnetic force pushing electrons in the moving charged object induces the emf.

See also

• Motional Emf using Faraday's Law: An expansion of this concept
• Lorentz Force: Combining electric and magnetic forces
• Generator: Real-world application
• Right-Hand Rule: How it works and other RHRs

Further reading

• Matter & Interactions, Vol 2
• The Feynman Lectures on Physics, Vol 2, Ch 16

External links

• Guide from MIT

References

• Matter & Interactions Vol 2
• MIT OpenCourseWare
• A Brief History of The Development of Classical Electrodynamics