Magnetic Field of a Solenoid Using Ampere's Law: Difference between revisions
Mchandler30 (talk | contribs) |
No edit summary |
||
| Line 1: | Line 1: | ||
Claimed by Mary Jane Chandler Fall 2016 | Claimed by Mary Jane Chandler Fall 2016 | ||
This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid. | Improved by Quinnell Smith Fall 2017 | ||
This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid, and the derivation of the formula of the magnetic field of a solenoid. | |||
==The Main Idea== | ==The Main Idea== | ||
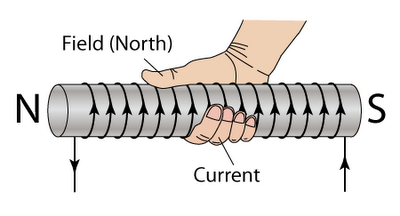
A solenoid is a cylindrical coil of wire that produces a uniform magnetic field when it is carrying an electric current. A solenoid is a form of an electromagnet that can create strong controlled magnetic fields throughout the coil except at the ends. Ampere's Law | A solenoid is a cylindrical coil of wire that produces a uniform magnetic field when it is carrying an electric current. A solenoid is a form of an electromagnet that can create strong controlled magnetic fields throughout the coil except at the ends.The magnetic field of solenoid can be solved by using Ampere's Law equation which relates the magnetic field surrounding the solenoid and the electric current. | ||
[[File:solenoidfrombook.png]] | [[File:solenoidfrombook.png]] | ||
Looking at the model, in the middle of the solenoid the field is constant throughout the entirety of the interior and is parallel to the axis. At the ends of a solenoid the magnetic field starts to point outward at varying angles. | |||
===Equation=== | ===Equation=== | ||
| Line 21: | Line 23: | ||
<math>{B = \frac{μ_{0}NI}{L}}</math> | <math>{B = \frac{μ_{0}NI}{L}}</math> | ||
The Right Hand Rule can be used to find the direction of the magnetic field by using your right hand and curling your fingers in the direction of the current | The Right Hand Rule can be used to find the direction of the magnetic field by using your right hand and curling your fingers in the direction of the current. The direction in which your thumb ends up pointing in after curling your fingers around the current, determines the direction of the magnetic. Keep in mind that the direction of the magnetic field will lie on the same axis as the length of the solenoid. | ||
[[File:Righthand.png]] | [[File:Righthand.png]] | ||
===Derivation of Equation=== | |||
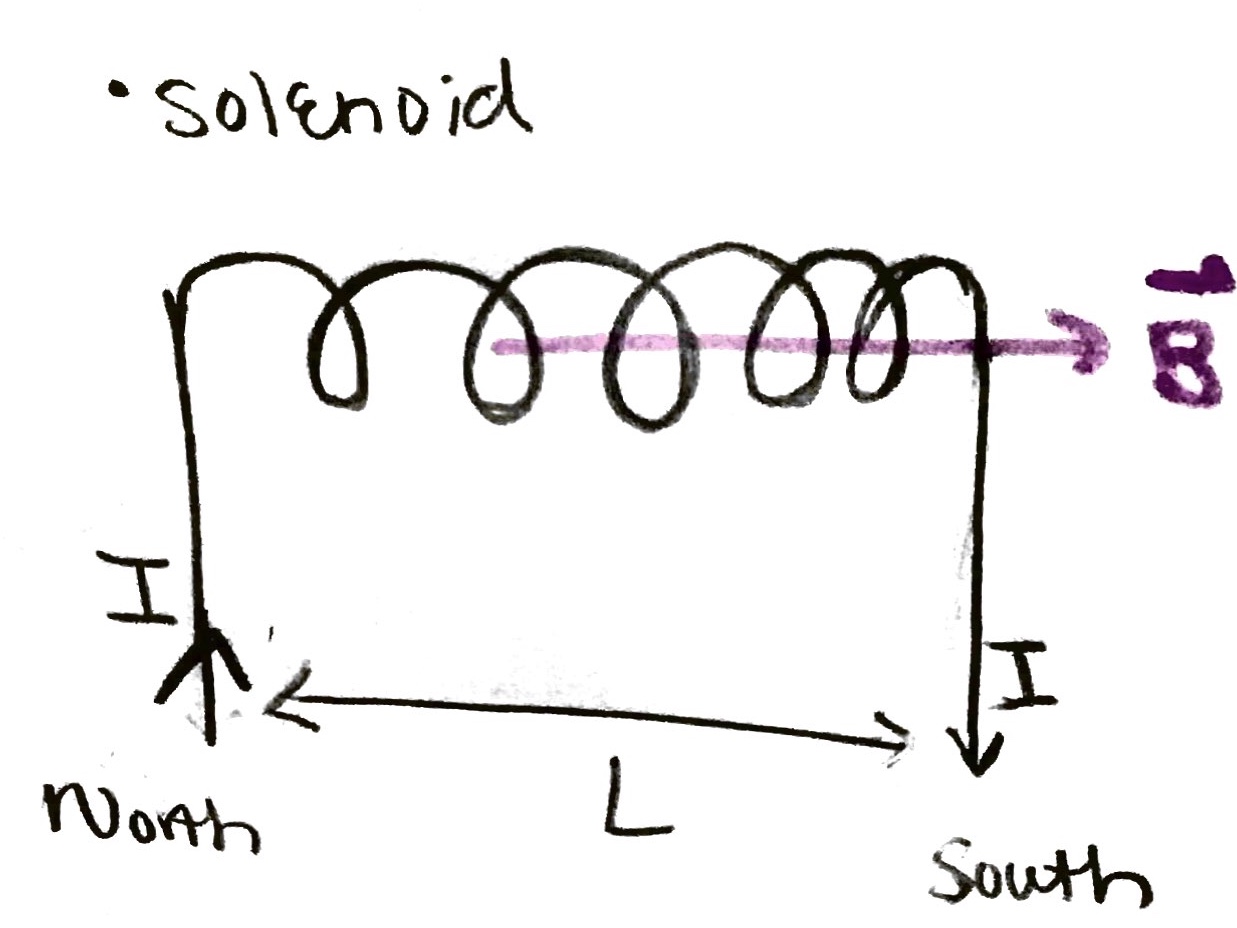
Looking at the equation of a solenoid, it could be difficult to understand how this equation was derived. Listed below are the steps taken to derive the equation and an image depicting what each symbol represents. | |||
[[File:step0.jpg]] | |||
Symbols: | |||
l:the length of the rectangular path decided to take to the length apply Ampere's Law | |||
L:the length of the solenoid | |||
B: the magnetic field of the solenoid | |||
N: the number of turns in the solenoid | |||
μ_0: a constant | |||
I: conventional current flowing through the solenoid | |||
Steps to Derive Equation: | |||
1. Apply Ampere's law could by finding the formula for relating the path of the current and magnetic field: Bl | |||
2. Find that Ampere's law is proportional to the path and solenoid's length proportionality times the number of turns in the solenoid and the electric current: <math>{Bl = \frac{μ_{0}NIl}{L}}</math> | |||
3.Cancel out the length of the path on each side of the equal sign to get the equation we use: <math>{B = \frac{μ_{0}NI}{L}}</math> | |||
==Examples== | ==Examples== | ||
| Line 54: | Line 85: | ||
*Must change 10 cm to .1 for the cm to m conversion | *Must change 10 cm to .1 for the cm to m conversion | ||
== | ==Connectedness== | ||
#Solenoids are important because they can create controlled magnetic fields making them useful for a variety of applications | #Solenoids are important because they can create controlled magnetic fields making them useful for a variety of applications. | ||
#As a | #As a mechanical engineering major solenoids are relevant to my major because mechanical engineers use solenoid components, and solenoid valves on a daily basis. An example of solenoids is a transformer which consists of a solenoid with different induced electric currents and number of turns which can perform step down or step up functionalities. | ||
==History== | |||
The history of Ampere's Law and its application for solenoids dates back to | |||
==See Also== | ==See Also== | ||
| Line 76: | Line 112: | ||
*http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html | *http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/solenoid.html | ||
*https://www.youtube.com/watch?v=MXuZ1SRjpqk | |||
*https://www.youtube.com/watch?v=xdsXP_l3q_0 | |||
==References== | ==References== | ||
Revision as of 01:30, 29 November 2017
Claimed by Mary Jane Chandler Fall 2016
Improved by Quinnell Smith Fall 2017
This page explains how to use Ampere's Law to solve for the magnetic field of a solenoid, and the derivation of the formula of the magnetic field of a solenoid.
The Main Idea
A solenoid is a cylindrical coil of wire that produces a uniform magnetic field when it is carrying an electric current. A solenoid is a form of an electromagnet that can create strong controlled magnetic fields throughout the coil except at the ends.The magnetic field of solenoid can be solved by using Ampere's Law equation which relates the magnetic field surrounding the solenoid and the electric current.
Looking at the model, in the middle of the solenoid the field is constant throughout the entirety of the interior and is parallel to the axis. At the ends of a solenoid the magnetic field starts to point outward at varying angles.
Equation
If there are [math]\displaystyle{ N }[/math] loops of wire that compose a solenoid of length [math]\displaystyle{ L }[/math], and we know that Ampere's Law gives us the form:
[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]
We can then solve for [math]\displaystyle{ B }[/math]:
[math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]
The Right Hand Rule can be used to find the direction of the magnetic field by using your right hand and curling your fingers in the direction of the current. The direction in which your thumb ends up pointing in after curling your fingers around the current, determines the direction of the magnetic. Keep in mind that the direction of the magnetic field will lie on the same axis as the length of the solenoid.
Derivation of Equation
Looking at the equation of a solenoid, it could be difficult to understand how this equation was derived. Listed below are the steps taken to derive the equation and an image depicting what each symbol represents.
Symbols:
l:the length of the rectangular path decided to take to the length apply Ampere's Law
L:the length of the solenoid
B: the magnetic field of the solenoid
N: the number of turns in the solenoid
μ_0: a constant
I: conventional current flowing through the solenoid
Steps to Derive Equation:
1. Apply Ampere's law could by finding the formula for relating the path of the current and magnetic field: Bl
2. Find that Ampere's law is proportional to the path and solenoid's length proportionality times the number of turns in the solenoid and the electric current: [math]\displaystyle{ {Bl = \frac{μ_{0}NIl}{L}} }[/math]
3.Cancel out the length of the path on each side of the equal sign to get the equation we use: [math]\displaystyle{ {B = \frac{μ_{0}NI}{L}} }[/math]
Examples
Solving for the Magnetic Field
Find the magnetic field produced by a 20 cm long solenoid if the number of loops is 200 and current passing through it is 8 A.
For this example all of the variables are given so it is just a simple math calculation using Ampere's Law, as given above, but for reiteration.
[math]\displaystyle{ {\oint\,\vec{B}•d\vec{l} = μ_{0}∑I_{inside path}} }[/math]
[math]\displaystyle{ {B = \frac{200*8}{.2}} }[/math] [math]\displaystyle{ {B = 8,000} }[/math]
Once you have solved for [math]\displaystyle{ B }[/math] all you have to do is find the direction of the magnetic field using the Right Hand Rule.
- Must convert 20 cm to .2 m
Solving for the Current
A solenoid has a magnetic field of 6x10-4 T, 2000 turns, and is 10 cm long. What is the current through the solenoid? For this example you are solving for I. Very similar to the above question, just rearranging the calculation of Ampere's Law.
[math]\displaystyle{ {I = \frac{LB}{μ_{0}N}} }[/math]
[math]\displaystyle{ {I = \frac{.1*6E-4}{2000}} }[/math] [math]\displaystyle{ {I = 3E-8 A} }[/math]
- Must change 10 cm to .1 for the cm to m conversion
Connectedness
- Solenoids are important because they can create controlled magnetic fields making them useful for a variety of applications.
- As a mechanical engineering major solenoids are relevant to my major because mechanical engineers use solenoid components, and solenoid valves on a daily basis. An example of solenoids is a transformer which consists of a solenoid with different induced electric currents and number of turns which can perform step down or step up functionalities.
History
The history of Ampere's Law and its application for solenoids dates back to
See Also
Magnetic Field of a Long Thick Wire Using Ampere's Law
Magnetic Field of Coaxial Cable Using Ampere's Law
Magnetic Field of a Toroid Using Ampere's Law
Further Reading
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley.
External Links
References
Chabay, Sherwood. (2015). Matter and Interactions (4th ed., Vol. 2). Raleigh, North Carolina: Wiley. Pg 887-888.