Bohr Model: Difference between revisions

Revision as of 20:15, 18 April 2018

CLAIMED BY WILLIAM DORAN (Spring 2018)

This page gives basic information about the Bohr model and quantization. It also includes examples using the Bohr model.

Main Idea

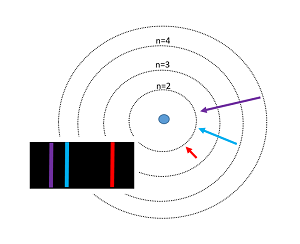
A visualization of the Bohr model and the hydrogen spectrum

The Bohr model of the atom was proposed by Niels Bohr in 1913, and it was radically different from any other models that previously existed. His model depicted atoms as having negatively charged electrons which orbited as small, positively charged nucleus. Bohr's incorporation of quantum theory was the most groundbreaking part; in this model, electrons can only exist in discrete energy levels, which are quantized. This model is very simplistic and is useful in introducing students to quantum mechanics. Although this model successfully predicts energy levels of the hydrogen atom, it has its shortcomings.

Bohr's Assumptions

Electrons travel in a circular orbit around the nucleus, similar to how planets orbit around the sun.
The energy that electrons have is related to their distance from the nucleus, or which energy level they occupy. The further away the electron, the more energy it has.
Electrons can gain or lose energy by jumping from one orbit to another. The energy is quantized - the orbitals have discreet radii, which Bohr called "stationary orbits."
When an excited electron returns back to its ground state, then it releases the energy that it absorbed, in the form of light. This quantized energy is equal to the difference between the energies of the orbits.

Stairs are a great way to visualize quantized energy. When you're going up stairs, you can only be standing on the steps, and not anywhere in between the steps. Similarly, energy can only be absorbed or emitted in specific quanta.

History

Ernest Rutherford proposed that the basic structure of an atom is a cloud of electrons which surround a small nucleus. With his experiments, he developed a model that depicted an atom like a solar system, with electrons orbiting around the nucleus. He proposed that the emission spectrum of hydrogen would look more like a smear rather than being made up of distinct lines. However, this was flawed, as it suggested that atoms can emit energy that isn't quantized. [8]

Rutherford's model of the atom, which Bohr expanded on

Niels Bohr, a physicist from Denmark, was able to explain the emission spectra of hydrogen by improving on the Rutherford model of the atom. In 1911 Bohr traveled to England in order to study the structure of atoms and molecules. There, he attended lectures on electromagnetism and worked with Rutherford and other scientists such as J. J. Thomson. When he returned to Denmark in 1912, Bohr noticed that in the atomic emissions spectrum of hydrogen, only certain colors could be seen. Thus, he theorized that electrons need to be in energy levels that are quantized. He related the energies of the colors he saw to the differences of hydrogen's energy levels. Although this model is not entirely correct, as it only applies to systems where two charged particles orbit each other, it still has many features that are very applicable to physics today. Later on, scientists such as Werner Heisenberg and Erwin Schrödinger worked to improve upon this model.[9]

Shortcomings of the Bohr Model

While the Bohr model is an important predecessor to the current quantum mechanical models of the atom, it doesn't correctly describe some aspects of electron orbitals. It does not provide any reasoning as to why certain spectral lines are brighter than others. Its main shortcoming is that it violates the uncertainty principle, as it considers electrons to have a definite radius and momentum. This model is very basic, and in order to know more specific details about spectra and charge distribution, more calculations must be done. Many of the failures of the Bohr model can be corrected by the Schrodinger equationfor the hydrogen atom.

Application

A Mathematical Model

The Angular Momentum Quantum

[math]\displaystyle{ ħ = h/2π =1.05*10^{-34} J*s }[/math]

h is Planck's constant, which is a physical constant that is essential in quantum mechanics.

Angular Momentum Is Quantized

[math]\displaystyle{ |\vec L_{trans,C}| = rp = Nħ }[/math]

p is the electron's momentum r is the radius of circular orbit N is an integer (1,2,3, ...)

We can derive the equation for r, the allowed Bohr radii for electron orbits.

1) Electric force the proton exerts on the electron: [math]\displaystyle{ F_{el} = {\frac{e^2}{4π ε0 r^2}} }[/math]

2) Using the momentum principle and curving motion: [math]\displaystyle{ |F_{perpendicular}| = {\frac{|p| |v|}{r}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

3)Substituting in Bohr's conditions: [math]\displaystyle{ {\frac{N^2 h*^2}{mr^3}} = {\frac{e^2}{4π ε0 r^2}} }[/math]

4)Solving for the allowed radii [math]\displaystyle{ r = {\frac{4π ε0 h*^2}{me^2}} *N^2 }[/math] where N = 1,2,3,...

Additionally, the formula for energy of hydrogen atom of different levels is also derived from this model.

E = K + Uelectric

1) [math]\displaystyle{ E = {\frac{mv^2}{2}} - {\frac{{\frac{1}{2}}*{\frac{1}{4π ε0}}*{\frac{me^2}{h*}}}{N^2}} }[/math]

2) [math]\displaystyle{ E = {\frac{13.6 eV}{N^2}} }[/math] where N = 1,2,3

Wavelengths

The Debroglie relationship can tell us about the wavelength associated with the electron: [math]\displaystyle{ λ = \frac{h}{mv} }[/math]

This equation is used to help derive the equation for the angular momentum of an electron in orbit [math]\displaystyle{ L = \frac{nh}{2π} }[/math]

A Computational Model

To interact with this glowscript visualization of the Bohr Model, click here. You will also find a graph of Energy (eV), Kinetic Energy, and Potential Energy. This visualization shows how the electrons jump from level to level according to the Bohr Model. There is also an energy vs distance graph shown which varies according to these levels. Notice that the further away the electron is, the more energy it has.

Examples

Simple

Find the magnitude of the translational angular momentum of an electron when a hydrogen atom is in its 2nd excited state above the ground state.

--

We know that the only possible states of the hydrogen atom are those when the electron's translational angular momentum is an integer multiple of ħ. [math]\displaystyle{ |\vec L_{trans,c}| = Nħ }[/math] For the 2nd excited state, N = 3 Now just plug the numbers in [math]\displaystyle{ |\vec L_{trans,c}| = (3)(1.05*10^{-34} J*s) = 3.15*10^{-34} J*s }[/math]

Middling

[6]A hydrogen atom is in state N = 3, where N = 1 is the lowest energy state. What is K+U in electron volts for this atomic hydrogen energy state?

1) [math]\displaystyle{ E(3) = {\frac{-13.6 eV}{3^2}} }[/math] = -1.51 Joules

2) [math]\displaystyle{ E(1) = {\frac{-13.6 eV}{1^2}} }[/math] = -13.6 Joules

3) K+U = energy of photon = [math]\displaystyle{ E(1) - E(3) = {\frac{-13.6 eV}{3^2}} - {\frac{-13.6 eV}{1^2}} }[/math] = 12.09 Joules

Below is the graph of E as the hydrogen atom goes from N = 3 to N = 1.

Difficult

Hydrogen has been detected transitioning from the 101^st to the 100^th energy levels. What is the wavelength of the radiation? Where in the electromagnetic spectrum is this emission?

To solve this problem, we first need to use formulas derived from Bohr Model of hydrogen atom. It is [math]\displaystyle{ E = {\frac{-13.6 eV}{N^2}} }[/math]

Then solve for the wavelength using formula from Electromagnetic Wave Theory.

This wavelength falls in the microwave portion of the electromagnetic spectrum.

Connectedness

I chose this topic because in our chemistry class, we learned a brief introduction to quantum mechanics, and this was one of the things that really interested me. I also really enjoyed the lab report we did involving this topic, and we got to use spectrometers to observe the emission spectrum of hydrogen and other elements. Bohr's discovery of this model was extremely important in the physics and chemistry world, because it laid down the framework for other theories in quantum mechanics. This model has applications to almost everything in our everyday lives - Bohr's notion that atoms emit light with very specific and quantized energies can explain how lasers work, and aid in figuring out what elements galaxies are made of, since every element has its own emission spectrum. Bohr's model has numerous amounts of applications to chemical engineering especially, because it explains why atoms have certain properties, such as conductivity. Every chemical process involves bonds between atoms being broken or formed.

[1] [2] [3] [4] [5] [6] [7] [8] [9] Note: All images on this page are either free for commercial use (with no attribution required) or made by myself.

Revision as of 13:39, 28 March 2017 (view source) Sguo70 (talk \| contribs) (→‎History) ← Older edit		Revision as of 20:15, 18 April 2018 (view source) Wdoran3 (talk \| contribs) No edit summary Newer edit →
Line 1:		Line 1:
	~~Sherry Guo~~ (Spring ~~2017~~)		'''CLAIMED BY WILLIAM DORAN (Spring 2018)'''

	This page gives basic information about the Bohr model and quantization. It also includes examples using the Bohr model.		This page gives basic information about the Bohr model and quantization. It also includes examples using the Bohr model.