Rutherford Experiment and Atomic Collisions

Claimed by: vhariharan8 (Spring 2017)

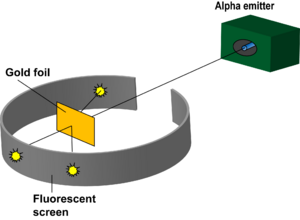
Rutherford's Gold Foil Experiment

Rutherford's Gold Foil Experiment helped detect that there was a large positively charged mass in the center of an atom. The experiment was done through the use of atomic collisions. Under the instruction of Rutherford, Hans Geiger and Ernest Marsden pointed a beam of alpha particles at a thin foil of metal and measured the scattering pattern by using a fluorescent screen. The scientists noted that some alpha particles bounced in random directions. This was not originally hypothesized due to the idea that, at most the alpha particle should experience only a 90° scattering angle. This helped lead to the discovery of the nucleus and a highly compact positively charged center.

A model of atomic collisions involving an alpha particle

History

Around the early 1900s, very little was known about atoms besides the ground breaking experiments conducted by J.J. Thompson in 1897. Thompson discovered what we call the electron. He hypothesized that electrons were negatively charged particles. It was also speculated that there must be a positive charge to balance out the negative charge from the electron. This "Plum Pudding Model" was invented by Thompson. This model assumed that matter consists of atoms which are overall positively charged, but with some type of negative electron charge throughout it. The electrons function as the "plum" which was evenly distributed through a positively charged "pudding".

In 1911, Ernest Rutherford, Hans Geiger, and Ernest Marsden carried out an experiment to test the plum pudding model. They shot alpha (helium 2+) particles at gold foil in order to measure the deflection of the particles as they come off of the other side. Rutherford created a method to record the position of each alpha particle by circling the bombarded object with a ZnS coated sheet. This sheet would emit a flash of light when hit by an alpha particle, allowing Rutherford to accurately measure the deflection of each alpha particle. He hypothesized that there would be a small amount of deflection due to the charge in the metal atom's subatomic particles. He noticed that some of the particles were deflected larger than 90 degrees. As a result, he was able to deduce that a majority of the particles went straight through the atom, but some of the particles bounced off of a small, positively charged mass in the center of the atom. This experiment helped indicate that the atom is made predominantly of empty space with a small nucleus with protons and electrons placed extremely far away from the nucleus in their own cloud.

A Mathematical Model

Rutherford modeled the effect the alpha particle has on the electrons of the gold atom. He did this by calculating the potential electric energy between the particle and the atom using the formula below.

[math]\displaystyle{ {U_{elec}} = {\frac{1}{4πε_0}}{\frac{q_{α}q_{Au}}{r}} }[/math]

Where:

r = center to center distance between particle and atom

[math]\displaystyle{ {\frac{1}{4πε_0}} = {9*10^9}{\frac {N*m^2}{C^2}} }[/math]

[math]\displaystyle{ {q_α} }[/math] = charge of alpha particle

[math]\displaystyle{ {q_{Au}} }[/math] = charge of gold nucleus

In this instance the charge of the alpha particle is equal to 2e and the charge of the gold particle is equal to 79e.

Another important part of atomic collisions is that they are inelastic collisions. This is shown by the conservation of both momentum and kinetic energy. Take the alpha particle and gold particle for example.

[math]\displaystyle{ {\vec{p_{α,i}}} = {\vec{p_{α,f}}}+ {\vec{p_{Au,f}}} }[/math]

[math]\displaystyle{ {\vec{K_{α,i}}} = {\vec{K_{α,f}}}+ {\vec{K_{Au,f}}} }[/math]

Where [math]\displaystyle{ {\vec{p}} }[/math] is momentum and [math]\displaystyle{ {\vec{K}} }[/math] is kinetic energy.

A Computational Model

Much like the mathematical model, the collision can be modeled computationally using the same formulas. In order to view this better, here is an example of one collision using the Rutherford Scattering Model.

Example Problems

Simple

Two protons start far apart. One has an initial momentum of [math]\displaystyle{ {\lt 5.1*10^{-4},0,0\gt }{kg*{\frac{m}{s}}} }[/math] and it approaches the other proton, at rest. The two protons repel each other and one now has a momentum of [math]\displaystyle{ {\lt 3.5*10^{-4},2.7*10^{-4},0\gt }{kg*{\frac{m}{s}}} }[/math]. What is the new momentum of the other proton?

Solution

[math]\displaystyle{ {\vec{p_{1,i}}}= {\lt 5.1*10^{-4},0,0\gt }{kg*{\frac{m}{s}}} }[/math]

[math]\displaystyle{ {\vec{p_{2,i}}}= {\lt 0,0,0\gt }{kg*{\frac{m}{s}}} }[/math]

[math]\displaystyle{ {\vec{p_{1,f}}}= {\lt 3.5*10^{-4},2.7*10^{-4},0\gt }{kg*{\frac{m}{s}}} }[/math]

[math]\displaystyle{ {\vec{p_{2,f}}}= {?} }[/math]

[math]\displaystyle{ {\vec{p_{tot,i}}}={\vec{p_{tot,f}}} }[/math]

[math]\displaystyle{ {\lt 5.1*10^{-4},0,0\gt }{kg*{\frac{m}{s}}+\lt 0,0,0\gt }{kg*{\frac{m}{s}}}={\lt 3.5*10^{-4},2.7*10^{-4},0\gt }{kg*{\frac{m}{s}}+{\vec{p_{2,f}}}} }[/math]

[math]\displaystyle{ {\lt 5.1*10^{-4},0,0\gt }{kg*{\frac{m}{s}}-\lt 3.5*10^{-4},2.7*10^{-4},0\gt }{kg*{\frac{m}{s}}}={\vec{p_{2,f}}} }[/math]

[math]\displaystyle{ {\vec{p_{2,f}}}={\lt 1.6*10^{-4},-2.7*10^{-4},0\gt }{kg*{\frac{m}{s}}} }[/math]

Meddling

A proton and an electron are a distance [math]\displaystyle{ {7.2*10^{-9}m} }[/math] apart. What is the electric potential energy of the system consisting of the proton and the electron?

Solution

[math]\displaystyle{ {U_{elec}} = {\frac{1}{4πε_0}}{\frac{q_{+}q_{-}}{r}} }[/math]

[math]\displaystyle{ {U_{elec}} = {9*10^{9}}{\frac {N*m^2}{C^2}}*{\frac{1.6*10^{-19}*(-1.6*10^{-19})}{7.2*10^{-9}}} = {-3.2*10^{-28}}{J} }[/math]

Connectedness

This topic is related to the study of chemical engineering. Without the discovery of the nucleus, any progress in this field would be limited based on the interaction of atomic particles. This would also hinder the field medicine for very similar reason. Much of the understanding of sciences has its roots in the understanding of the atom and its functions. This experiment and the idea of atomic collisions helped to widen the atomic grasp. One of the best industrial examples of the is the Large Hadron Collider.

History

With the knowledge of the plum pudding model of the atom, Ernst Rutherford and a small group of scientists set out to discover the properties behind alpha particles. The experiment, now known as the Gold Foil Experiment, was used to test this in 1911. It involved launching alpha particles at a small piece of gold foil. It was hypothesized that the alpha particle would be deflected at times, but at an angle because it was assumed that the alpha particle was more dense than the gold foil atom. They registered deflected particles through light emissions that would occur when the alpha particle hit the light source. Much to their surprise, some of the alpha particles they launched bounced straight back. This demonstrated that the gold particle was more massive than expected. It led to the discovery that the atom contained a positively charged nucleus. This was a major break through in the study of the atom in that it showed what the atoms composition was and how it act around other atoms.

Above is a model of the Gold Foil experiment performed in Rutherford's lab.

References

"History of Rutherford Experiment". HyperPhysics. Web. 03 Dec. 2015. Retrieved from: <http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html>.

Chabay, R.W., & Sherwood, B.A. (2015). Collisions. In Fiorillo, J. Editor & Rentrop, A. Editor (Eds.), Matter and Interactions (383-410). John Wiley & Sons, Inc.