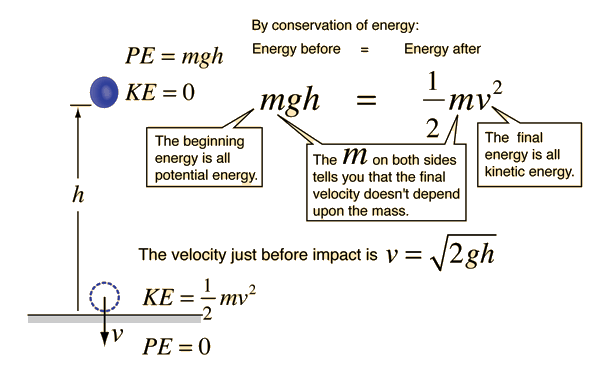Conservation of Energy

Kyle Barber (kbarber8) claimed 03/26/2017

This page was originally created by ksubramanian33, as can be seen by the edit history.

Main Ideas

• Conservation of energy mean that the total energy of a system will be the same before and after an event.
• This only applies to isolated systems (no outside forces acting on the system).
  • Not Isolated: An object sliding across a rough floor (system = the object). There is work being done by the floor on the object because of the frictional force.
  • Isolated: An object sliding across a rough floor (system = the object AND the floor). There is no work done on the system because all the forces are contained in the system.

Main Types of Energy

• Single Particle
  • Particle Energy
  • Rest Energy
  • Kinetic (particle)
• General Objects
  • Kinetic: [math]\displaystyle{ \frac{1}{2} m v \lt sup\gt 2\lt /sup\gt }[/math]
  • Gravitational Potential:
  • Spring (Elastic) Potential:
  • Thermal Energy:

General Formulas

For any given isolated system, the total energy will remain constant regardless of any processes or interactions that occur in the domain. Therefore, energy cannot be created or destroyed.

The change in Energy=Q+W
See Reference 1 A Mathematical Model

The most general mathematical formula to model the conservation of energy is E_initial = E_final where E is the total energy of the system.
More specifically, the total energy of the system can be described as the sum of the kinetic and potential energies. E = K + U where K is the total kinetic energy and U is the total potential energy.
From this, you can infer that for an isolated system, any change in kinetic energy will correspond in an equal but opposite change in the potential energy and vice versa.

The above model is only applicable in an ideal, frictionless world without heat transfers. However, the adjustments needed to account for friction and heat are easy to include. For an isolated system with friction, E_initial - W + Q = E_final where W is the work done by friction and Q is the heat added to the system. In this case, W and Q are provided by the surroundings of the system.

See Reference 2

A Computational Model The following demonstration provides a computer model that shows the changes in the different types of energy of the skater. In the initial simulation, there is no friction, so the energy changes between kinetic and potential, while the total energy remains constant. In the second simulation, friction is introduced, which results in thermal energy being created. This energy is then dissipated into the surroundings so the system of the skater loses total energy, but the total energy of the skater AND the surroundings still remains constant.

Skater

Examples

Simple

A ball is at rest on a table with 50 J of potential energy. 
It then rolls of the table, and at one point in time as it falls, the ball has 30 J of kinetic energy. 

What is the potential energy of the ball at that instant?

See Reference 3

E_initial = E_final
K_initial + U_initial = K_final + U_final
0 J + 50 J = 30 J + U_final
U_final = 20 J

Middling

A ball is at rest 50 m above the ground. You then drop the ball.
What is its speed before hitting the ground? 

See Reference 4

v = √2gh 
v = √2(9.8)(50) 
v = 31.3 m/s

Difficult

The driver of an SUV (m = 1700 kg) isn’t paying attention and rear ends a car (m = 950 kg) on level ground at a red light.
On impact, both drivers lock their brakes. The SUV and car stick together and travel a distance of 8.2 m before they
come to a stop. How fast was the SUV traveling just before the collision? The coefficient of friction between the tires and
the road is 0.72.

See Reference 5

Notice how the mass is canceled.

Connectedness

Computer Science
1. How is this topic connected to something that you are interested in?
This concept is clearly connected to physics, which overall helps explain and sometimes predict how our world works. Knowing why and how things happen around me is something I find interesting since I can say it affects my daily life.
2. How is it connected to your major?
This topic is connected to computer science in the field of modeling and simulation. When you use computers to more efficiently model grand scale scenarios, it is important to take all fundamental concepts of physics, including the conservation of energy, into account.
3. Is there an interesting industrial application?
The law of conservation of energy is prevalent in nearly every industrial application of physics. More specifically, it is relevant today as finding renewable and sustainable forms of energy is becoming a more prevalent social and economic issue. It will be interesting to see how this concept will be applied as we try to get more energy for less.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
Who: Julius Robert Mayer
What: Most formally discovered the law of conservation of energy
When: 1842
Where: Germany
Why: To explain what happens to energy in an isolated system
See Reference 6

See also

Kinetic Energy
Potential Energy
Work

Further reading

Goldstein, Martin, and Inge F., (1993). The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.
Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
Nolan, Peter J. (1996). Fundamentals of College Physics, 2nd ed. William C. Brown Publishers.

External links

The First Law of Thermodynamics

References

1."Conservation of Energy." Hmolpedia. Web. 1 Dec. 2015. <http://www.eoht.info/page/Conservation+of+energy>.
2. "University of Wisconsin Green Bay." Speed & Stopping Distance of a Roller-Coaster. Web. 1 Dec. 2015. <http://www.uwgb.edu/fenclh/problems/energy/2/>.
3. "Motion." G9 to Engineering. Web. 1 Dec. 2015. <http://www.g9toengineering.com/resources/translational.htm>.
4. "Energy of Falling Object." HyperPhysics. Web. 1 Dec. 2015. <http://hyperphysics.phy-astr.gsu.edu/hbase/flobj.html>.
5. "Conservation of Energy & Momentum Problem: Collision of Two Cars at a Stoplight." University of Wisconsin- Green Bay Physics. Web. 2 Dec. 2015. <http://www.uwgb.edu/fenclh/problems/energy/6/>.
6. "Law of Conservation of Mass Energy." Law of Conservation of Mass Energy. Web. 3 Dec. 2015. <http://www.chemteam.info/Thermochem/Law-Cons-Mass-Energy.html>.