Point Charge: Difference between revisions
mNo edit summary |
No edit summary |
||
| Line 4: | Line 4: | ||
==The Main Idea== | ==The Main Idea== | ||
Every charge creates its own electric field. The two known elementary charges are the proton and electron, both of which are modeled as point charges. The electric field for point charges points radially outward in the case of the proton, and radially inward in the case of the electron. The field is calculated using Coulomb's Law. Indeed, the electric field is defined as a vector field that associates each point in space with the electric force that an infinitesimal test charge would experience. The source of the electric field in this article is the point charge. | |||
| Line 16: | Line 16: | ||
<math>\vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r</math> | <math>\vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r</math> | ||
Which is derived from [[Gauss's Law]], modelling the point charge as a sphere. | |||
, | |||
<math>{\epsilon_0} </math> is a constant representing vacuum permittivity, the permittivity of free space, or the electric constant, and is approximately <math>8.854*10^{-12}\frac{C^2}{N m^2}</math> | |||
Below is a visual representation of electric | <math>\frac{1}{4 \pi \epsilon_0 } </math> is known as Coulomb's Constant and is approximately <math>8.987*10^{9}\frac{N m^2}{C^2} </math> | ||
'''''r''''' is the magnitude of the distance between the observation location and the source location | |||
, '''''q''''' is the charge of the particle | |||
and <math>\hat r </math> is the unit vector in the direction of the distance from the source location to the observation point. | |||
The force on a given test charge is governed by <math> F = Eq </math> where '''''E''''' is the electric field and '''''q''''' is the charge of a test charge in Coulombs. This can be represented by Coulomb's Law: | |||
<math> F = \frac{1}{4 \pi \epsilon_0 } \frac{q_1 q_2}{r^2} \hat r </math> | |||
By solving for the electric field in <math> F = Eq </math> modeled as Coulomb's Law, one obtains the equation for the electric field of the point charge: | |||
<math> E = \frac{F}{q_2} = \frac{1}{4 \pi \epsilon_0 } \frac{q_1}{r^2} \hat r </math> | |||
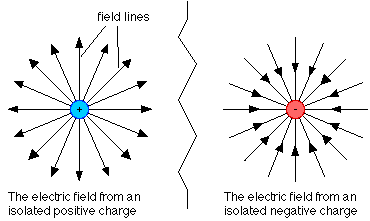
Below is a visual representation of electric field lines due to a positive and negative point charge | |||
[[File:Point_charge.GIF]] | [[File:Point_charge.GIF]] | ||
| Line 33: | Line 45: | ||
===A Computational Model=== | ===A Computational Model=== | ||
Below is a link to some code which can help visualize the Electric Field due to a proton. | |||
https://trinket.io/glowscript/725d552305 | |||
Notice how the arrows grow by a factor of <math> \frac{1}{r^{2}} </math> as the observation location gets closer to the proton. | |||
| Line 46: | Line 57: | ||
===Simple=== | ===Simple=== | ||
There is an electron at | There is an electron at the origin. Calculate the electric field at (4,-3,1)m. | ||
'''Step 1:''' Find <math>\hat r</math> | '''Step 1:''' Find <math>\hat r</math> | ||
Find <math>\vec r_{obs} - \vec r_{electron} ( | Find <math>\vec r_{obs} - \vec r_{electron} ((4,-3,1) - (0,0,0) = <4,-3,1> </math>m | ||
Calculate the magnitude of r. (<math>\sqrt{4^2+(-3)^2+1^2}=\sqrt{26}</math> | Calculate the magnitude of <math>\vec r</math>. (<math>\sqrt{4^2+(-3)^2+1^2}=\sqrt{26}</math> | ||
From r, find the unit vector <math>\hat{r}.</math> <math> <\frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}> </math> | From <math>\vec r</math>, find the unit vector <math>\hat{r}.</math> <math> <\frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}> </math> | ||
'''Step 2:''' Find the magnitude of the Electric Field | '''Step 2:''' Find the magnitude of the Electric Field | ||
| Line 62: | Line 73: | ||
'''Step 3:''' Multiply the magnitude of the Electric Field by <math>\hat{r}</math> to find the Electric Field | '''Step 3:''' Multiply the magnitude of the Electric Field by <math>\hat{r}</math> to find the Electric Field | ||
<math>E = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*<\frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}> = <-4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}> N/C </math> | |||
===Middling=== | ===Middling=== | ||
A particle of unknown charge is located at | A particle of unknown charge is located at (-0.21, 0.02, 0.11) m. Its electric field at point (-0.02, 0.31, 0.28) m is <math><0.124, 0.188, 0.109> </math> N/C. Find the magnitude and sign of the particle's charge. | ||
Given both an observation location and a source location, one can find both r and <math>\hat{r}</math> Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge,<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math> one can find the magnitude and sign of the charge. | |||
'''Step 1:''' | '''Step 1:''' | ||
Find <math>\vec r_{obs} - \vec r_{particle} | Find <math>\vec r_{obs} - \vec r_{particle} </math>. | ||
<math>\vec r = (-0.02,0.31,0.28) m - (-0.21,0.02,0.11) m = <0.19,0.29,0.17> m </math> | |||
To find <math>\vec r_{mag} </math>, find the magnitude of <math><0.19,0.29,0.17></math> | |||
<math>\sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39</math> | |||
'''Step 2:''' Find the magnitude of the Electric Field | |||
<math>E= <0.124, 0.188, 0.109> N/C</math> | |||
<math>E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25</math> | |||
'''Step 3:''' Find q by rearranging the equation for E_{mag} | '''Step 3:''' Find '''''q''''' by rearranging the equation for <math>E_{mag}</math> | ||
<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math> | <math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math> | ||
| Line 90: | Line 106: | ||
By rearranging this equation we get | By rearranging this equation we get | ||
<math> q= {4 pi epsilon_0 } *{r^2}*E_{mag} </math> | <math> q= {4 pi * epsilon_0 } *{r^2}*E_{mag} </math> | ||
<math> q= {1/(9*10^9)} *{.39^2}*.25 </math> | <math> q= {1/(9*10^9)} *{0.39^2}*0.25 </math> | ||
q= 4.3*10^-12 C | <math> q= + 4.3*10^{-12} C </math> | ||
===Difficult=== | ===Difficult=== | ||
The electric | The electric force on a -2mC particle at a location (3.98 , 3.98 , 3.98) m due to a particle at the origin is <math>< -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}></math> N. What is the charge on the particle at the origin? | ||
Given the force and charge on the particle, one can calculate the surrounding electric field. With this variable found, this problem becomes much like the last one. | |||
<math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} </math> | <math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} </math> | ||
| Line 110: | Line 128: | ||
Find the magnitude of the Electric field. | Find the magnitude of the Electric field. | ||
<math> | <math> F = Eq </math> | ||
<math> | <math> <5.5*10^{3}, -7.6*10^{3}, 0> = E * -2mC </math> | ||
<math> E = \frac{< -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}>}{-2mC} = <2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}> </math> N/C | |||
<math> r_{ | '''Step 2:''': | ||
Find <math>\vec r_{obs} - \vec r_{particle} </math>. | |||
<math> | <math>\vec r = (3.98 , 3.98 , 3.98) m - (0 , 0 , 0) m = <3.98 , 3.98 , 3.98> m </math> | ||
To find <math>\vec r_{mag} </math>, find the magnitude of <math><3.98 , 3.98 , 3.98></math> | |||
<math>\sqrt{3.98^2+3.98^2+3.98^2}=\sqrt{47.52}= 6.9</math> | |||
'''Step 3:''' Find the magnitude of the Electric Field | |||
<math> | <math>E= <2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}> </math> N/C | ||
<math>E_{mag} = (\sqrt{(2.75*10^{6})^2+2.75*10^{6})^2+2.75*10^{6})^2}=\sqrt{2.27*10^{13}}=4.76*10^{6}</math> | |||
<math> | '''Step 4:''' Find '''''q''''' by rearranging the equation for <math>E_{mag}</math> | ||
<math> r | <math> E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} </math> | ||
By rearranging this equation we get | |||
<math> | <math> q= {4 pi * epsilon_0 } *{r^2}*E_{mag} </math> | ||
<math> | <math> q= {1/(9*10^9)} *{6.9^{2}}*4.76*10^{6} </math> | ||
<math> | <math> q= + 0.253 C </math> | ||
| Line 164: | Line 172: | ||
1.How is this topic connected to something that you are interested in? | 1.How is this topic connected to something that you are interested in? | ||
This topic is the most very basic aspect of physics relating to electricity and magnetism. As someone who is very interested in physics, this topic is important to understanding how more complex ideas that come in later on chapters work. | |||
2.How is it connected to your major? | 2.How is it connected to your major? | ||
As a mechanical engineer, static charges don't relate to what I do all that much, but the vector algebra certainly does. | |||
3.Is there an interesting industrial application? | 3.Is there an interesting industrial application? | ||
The electric field of a point particle and the [[Superposition Principle]] are integral in understanding the interactions of many charges in various situations, such as a charged sphere or rod. Understanding the way charges behave is important in working with electricity. | |||
==History== | ==History== | ||
| Line 186: | Line 195: | ||
[[Electric Field]] <br> | [[Electric Field]] <br> | ||
[[Electric Force]] | [[Electric Force]] <br> | ||
[[Superposition Principle]] | |||
===Further reading=== | ===Further reading=== | ||
Revision as of 01:58, 9 April 2017
This page is all about the Electric Field due to a Point Charge.CLAIMED BY Richard Granger 4-8-2017 == Electric Field==
The Main Idea
Every charge creates its own electric field. The two known elementary charges are the proton and electron, both of which are modeled as point charges. The electric field for point charges points radially outward in the case of the proton, and radially inward in the case of the electron. The field is calculated using Coulomb's Law. Indeed, the electric field is defined as a vector field that associates each point in space with the electric force that an infinitesimal test charge would experience. The source of the electric field in this article is the point charge.
A Mathematical Model of Electric Field due to Point Charge
The Electric Field of a Point Charge can be found by using the following formula:
[math]\displaystyle{ \vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} \hat r }[/math]
Which is derived from Gauss's Law, modelling the point charge as a sphere.
[math]\displaystyle{ {\epsilon_0} }[/math] is a constant representing vacuum permittivity, the permittivity of free space, or the electric constant, and is approximately [math]\displaystyle{ 8.854*10^{-12}\frac{C^2}{N m^2} }[/math]
[math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } }[/math] is known as Coulomb's Constant and is approximately [math]\displaystyle{ 8.987*10^{9}\frac{N m^2}{C^2} }[/math]
r is the magnitude of the distance between the observation location and the source location , q is the charge of the particle and [math]\displaystyle{ \hat r }[/math] is the unit vector in the direction of the distance from the source location to the observation point.
The force on a given test charge is governed by [math]\displaystyle{ F = Eq }[/math] where E is the electric field and q is the charge of a test charge in Coulombs. This can be represented by Coulomb's Law:
[math]\displaystyle{ F = \frac{1}{4 \pi \epsilon_0 } \frac{q_1 q_2}{r^2} \hat r }[/math]
By solving for the electric field in [math]\displaystyle{ F = Eq }[/math] modeled as Coulomb's Law, one obtains the equation for the electric field of the point charge:
[math]\displaystyle{ E = \frac{F}{q_2} = \frac{1}{4 \pi \epsilon_0 } \frac{q_1}{r^2} \hat r }[/math]
Below is a visual representation of electric field lines due to a positive and negative point charge
A Computational Model
Below is a link to some code which can help visualize the Electric Field due to a proton.
https://trinket.io/glowscript/725d552305
Notice how the arrows grow by a factor of [math]\displaystyle{ \frac{1}{r^{2}} }[/math] as the observation location gets closer to the proton.
Examples
Simple
There is an electron at the origin. Calculate the electric field at (4,-3,1)m.
Step 1: Find [math]\displaystyle{ \hat r }[/math]
Find [math]\displaystyle{ \vec r_{obs} - \vec r_{electron} ((4,-3,1) - (0,0,0) = \lt 4,-3,1\gt }[/math]m
Calculate the magnitude of [math]\displaystyle{ \vec r }[/math]. ([math]\displaystyle{ \sqrt{4^2+(-3)^2+1^2}=\sqrt{26} }[/math]
From [math]\displaystyle{ \vec r }[/math], find the unit vector [math]\displaystyle{ \hat{r}. }[/math] [math]\displaystyle{ \lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt }[/math]
Step 2: Find the magnitude of the Electric Field
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26} }[/math]
Step 3: Multiply the magnitude of the Electric Field by [math]\displaystyle{ \hat{r} }[/math] to find the Electric Field
[math]\displaystyle{ E = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*\lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt = \lt -4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}\gt N/C }[/math]
Middling
A particle of unknown charge is located at (-0.21, 0.02, 0.11) m. Its electric field at point (-0.02, 0.31, 0.28) m is [math]\displaystyle{ \lt 0.124, 0.188, 0.109\gt }[/math] N/C. Find the magnitude and sign of the particle's charge.
Given both an observation location and a source location, one can find both r and [math]\displaystyle{ \hat{r} }[/math] Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge,[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] one can find the magnitude and sign of the charge.
Step 1: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math].
[math]\displaystyle{ \vec r = (-0.02,0.31,0.28) m - (-0.21,0.02,0.11) m = \lt 0.19,0.29,0.17\gt m }[/math]
To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 0.19,0.29,0.17\gt }[/math]
[math]\displaystyle{ \sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39 }[/math]
Step 2: Find the magnitude of the Electric Field
[math]\displaystyle{ E= \lt 0.124, 0.188, 0.109\gt N/C }[/math]
[math]\displaystyle{ E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25 }[/math]
Step 3: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]
By rearranging this equation we get
[math]\displaystyle{ q= {4 pi * epsilon_0 } *{r^2}*E_{mag} }[/math]
[math]\displaystyle{ q= {1/(9*10^9)} *{0.39^2}*0.25 }[/math]
[math]\displaystyle{ q= + 4.3*10^{-12} C }[/math]
Difficult
The electric force on a -2mC particle at a location (3.98 , 3.98 , 3.98) m due to a particle at the origin is [math]\displaystyle{ \lt -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}\gt }[/math] N. What is the charge on the particle at the origin?
Given the force and charge on the particle, one can calculate the surrounding electric field. With this variable found, this problem becomes much like the last one.
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]
to find the rmag value. To find [math]\displaystyle{ \hat r }[/math] we can find the direction of the electric field as that is obviously going to be in the same direction as [math]\displaystyle{ \hat r }[/math]. Then, once we find [math]\displaystyle{ \hat r }[/math], all that is left to do is multiply [math]\displaystyle{ \hat r }[/math] by rmag and that will give us the [math]\displaystyle{ r }[/math] vector. We can then find the location of the particle as we know [math]\displaystyle{ r=r_{observation}-r_{particle} }[/math]
Step 1: Find the magnitude of the Electric field.
[math]\displaystyle{ F = Eq }[/math]
[math]\displaystyle{ \lt 5.5*10^{3}, -7.6*10^{3}, 0\gt = E * -2mC }[/math]
[math]\displaystyle{ E = \frac{\lt -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}\gt }{-2mC} = \lt 2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}\gt }[/math] N/C
Step 2:: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math].
[math]\displaystyle{ \vec r = (3.98 , 3.98 , 3.98) m - (0 , 0 , 0) m = \lt 3.98 , 3.98 , 3.98\gt m }[/math]
To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 3.98 , 3.98 , 3.98\gt }[/math]
[math]\displaystyle{ \sqrt{3.98^2+3.98^2+3.98^2}=\sqrt{47.52}= 6.9 }[/math]
Step 3: Find the magnitude of the Electric Field
[math]\displaystyle{ E= \lt 2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}\gt }[/math] N/C
[math]\displaystyle{ E_{mag} = (\sqrt{(2.75*10^{6})^2+2.75*10^{6})^2+2.75*10^{6})^2}=\sqrt{2.27*10^{13}}=4.76*10^{6} }[/math]
Step 4: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]
[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]
By rearranging this equation we get
[math]\displaystyle{ q= {4 pi * epsilon_0 } *{r^2}*E_{mag} }[/math]
[math]\displaystyle{ q= {1/(9*10^9)} *{6.9^{2}}*4.76*10^{6} }[/math]
[math]\displaystyle{ q= + 0.253 C }[/math]
Connectedness
1.How is this topic connected to something that you are interested in?
This topic is the most very basic aspect of physics relating to electricity and magnetism. As someone who is very interested in physics, this topic is important to understanding how more complex ideas that come in later on chapters work.
2.How is it connected to your major?
As a mechanical engineer, static charges don't relate to what I do all that much, but the vector algebra certainly does.
3.Is there an interesting industrial application?
The electric field of a point particle and the Superposition Principle are integral in understanding the interactions of many charges in various situations, such as a charged sphere or rod. Understanding the way charges behave is important in working with electricity.
History
Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.
Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.
See also
Electric Field
Electric Force
Superposition Principle
Further reading
Principles of Electrodynamics by Melvin Schwartz ISBN: 9780486134673
Electricity and Magnetism: Edition 3 , Edward M. Purcell David J. Morin
External links
Some more information : http://hyperphysics.phy-astr.gsu.edu/hbase/electric/epoint.html
http://www.physics.umd.edu/courses/Phys260/agashe/S10/notes/lecture18.pdf
References
Matter and Interactions Vol. II
PY106 Notes. (n.d.). Retrieved November 27, 2016, from http://physics.bu.edu/~duffy/py106.html
Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution