Light Propagation Through a Medium: Difference between revisions
No edit summary |
No edit summary |
||
| Line 23: | Line 23: | ||
What is the index of refraction of a refractive medium if the angle of incidence in air is 30 degrees and the angle of refraction is 15 degrees. | What is the index of refraction of a refractive medium if the angle of incidence in air is 30 degrees and the angle of refraction is 15 degrees. | ||
====Solution==== | ====Solution==== | ||
(1*sin(30))/sin(15) = 1.93 | |||
===Difficult=== | ===Difficult=== | ||
Revision as of 12:09, 24 November 2017
This page is going to be about about Light Propagation. A work in progress . Edited by Roshan Konda Fall 2017
The Main Idea
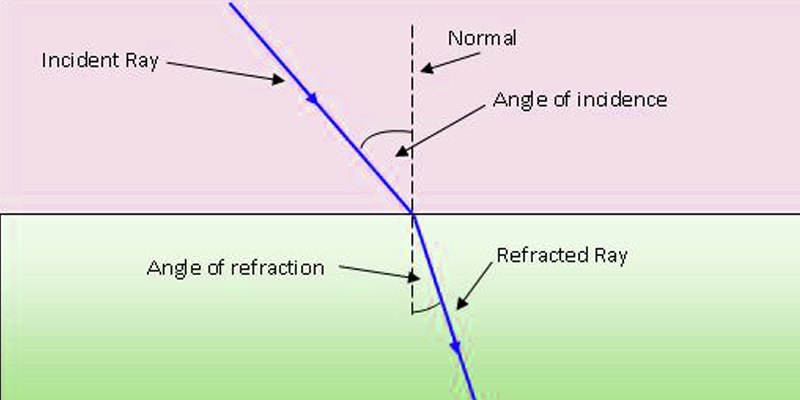
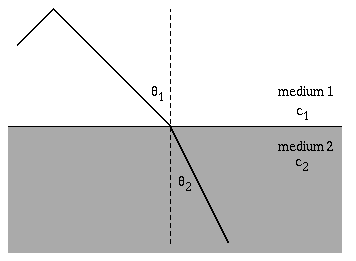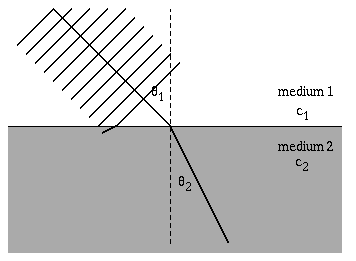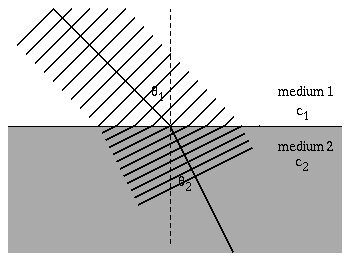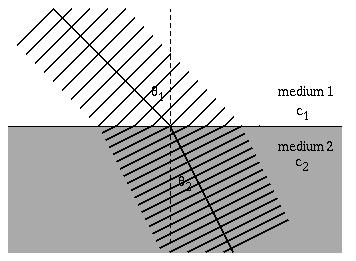
When light travels through anything but a vacuum the speed of light travels at a speed different from c=3.00E8 m/s and the light particles scatter. The highest speed that light can travel though is the universal constant c. Light also refracts, or changes direction when it enters a new medium.
A Mathematical Model
The speed of light through a medium can be given by the formula n=(c/v), where n is the index of refraction, v is the velocity of light through the medium and c is the speed of light through a vacuum. The relationship between the angle of incidence and angle of refraction when light passes through a medium is given by Snell's Law. n1sin(theta1) = n2sin(theta2)
A Computational Model
Examples
Easy
The speed of light is measured to be 2.76E8 m/s, What is the index of refraction for the medium?
Solution
The index of refraction is n=(c/v), n=(3.00E8)/(2.76E8) = 1.09.
Medium
What is the index of refraction of a refractive medium if the angle of incidence in air is 30 degrees and the angle of refraction is 15 degrees.
Solution
(1*sin(30))/sin(15) = 1.93