Translational, Rotational and Vibrational Energy: Difference between revisions

Revision as of 13:45, 24 November 2017

Claimed by Ferguson Beardsley Fall 2017

Main Idea

In many cases, analyzing the kinetic energy of an object is in fact more difficult than just applying the formula [math]\displaystyle{ K = \cfrac{1}{2}mv^2 }[/math]. An example of this is when throwing a basketball because not only does it move through the air but it is also rotating around its own axis. When analyzing more complicated movements like this one, it is necessary to break kinetic energy into different parts, such as rotational, translational, and vibrational, and analyze each one separately.

Translational kinetic energy is the kinetic energy associated with the motion of the center of mass of an object. This would be the basketball traveling in the air from one location to another. While relative kinetic energy is the kinetic energy associated to the rotation or vibration of the atoms of the object around its center or axis. Relative kinetic energy would be the rotation of the basketball around it's axis. Later on this page, we go into more depth about the different types of kinetic energy.

Here is a link to a video which explains kinetic energy in detail: [1]

Kinetic Energy

Total Kinetic Energy

As we just saw, the total kinetic energy of a multi particle system can be divided into the energy associated with motion of the center of mass and the motion of the center of mass. [2]

[math]\displaystyle{ K_{total} = K_{translational} + K_{relative} }[/math]

The relative kinetic energy is composed of motion due to rotation about the center of mass and vibrations/oscillations of the object. [3] [math]\displaystyle{ K_{total} = K_{translational} + K_{rotational} + K_{vibrational} }[/math]

Calculating Translational Kinetic Energy

"Translation" means to move from one location to another location. By calculating translational kinetic energy, we can track how one object moves from one location to another. Since the translational kinetic energy is associated to the movement of the center of mass of the object, it is important to know how to calculate the location of the center of mass and the velocity of the center of mass which is shown in the two equations below:

[math]\displaystyle{ r_{CM} = \cfrac{m_1r_1 + m_2r_2+m_3r_3 + ...}{m_1 + m_2 +m_3} }[/math] [math]\displaystyle{ v_{CM} = \cfrac{m_1v_1 + m_2v_2+m_3v_3 + ...}{m_1+ m_2 +m_3} }[/math][4]

Here is a link to video if you want to refresh knowledge one center of mass: [5]

The motion of canter of mass is described by the velocity of center of mass. Using the total mass and the velocity of the center of mass, we :

[math]\displaystyle{ K_{translational} = \cfrac{1}{2}M_{total}v_{CM}^2 }[/math][6]

Calculating Vibrational Kinetic Energy

The total energy due to vibrations is the sum of the potential energy associated with interaction causing the vibrations and the kinetic energy of the vibrations.

[math]\displaystyle{ E_{vibrational} = K_{vibrational} +U_{s} }[/math]

The easiest way to find vibrational kinetic energy is by knowing the other energy terms and isolating the vibrational kinetic energy. This is when there is no rotational kinetic energy:

[math]\displaystyle{ E_{total} = K_{trans} + K_{vibrational} + U_{s} +E_{rest} }[/math] [math]\displaystyle{ K_{vibrational} = E_{total} - (K_{trans} + U_{s} +E_{rest}) }[/math]

Calculating Rotational Kinetic Energy

Rotational kinetic energy is the energy due to the rotation about center of mass and can be calculated by finding the angular momentum and inertia, which be discussed in greater detail in the next two sections. The equation used to find kinetic rotational energy is below:

[math]\displaystyle{ K_{rotational} =1/2I_{cm}{w}^2 }[/math]

Here are links to two videos that cover rotational kinetic energy and moment of interim: [7][8]

Calculating Moment of Inertia

The moment of inertia of an object shows the difficulty of rotating an object, since the larger moment of inter the more energy required to rotate the object at the same angular velocity as an object with smaller moment of inertia. It is the sum of the products of the mass of each particle in the object with the square of their distance from the axis of rotation. The general formula for calculating the moment of inertia of an object is:

[math]\displaystyle{ I = m_1r_{\perp,1}^2 + m_2r_2{\perp,2}^2 + m_3r_{\perp,3}^2 +... }[/math] Units: [math]\displaystyle{ kg.m^2 }[/math]

Here [math]\displaystyle{ r_1, r_2, r_3 }[/math] represent the perpendicular distance from the point/axis of rotation.

Moment of Inertia is actually calculated using Calculus. These values we obtain for standard objects are not once you will need to derive, but conceptually understanding how they come to be will help you understand Moment of Inertia and it's impact on a solid. Below are a few moment of inertia used most frequently

File:Https://cnx.org/resources/4c906c92cebe30d9486deb2a682acf561d23c9c1

When you compare two bodies rotating with the same kinetic energy and one of them has a higher moment of Inertia, then the one with the higher moment of Inertia has a lower speed. If angular speed is lower and radius is larger that means mass must be small since Moment of Inertia also depends on mass and distance from axis of rotation. So we can deduce such relations which helps us understand how the moment of Inertia of an object actually affects the object in different ways.

Angular Speed

The angular speed is that rate at which the object is rotating. It is given in the following formula: [math]\displaystyle{ \omega = \cfrac{2\pi}{T} }[/math]]

The angle which the disk turns is 2 pi in a time T. It is measured in units in radians per second. The tangential velocity of an object is related to some distance r and at the angular speed because the tangential velocity increases when the distance from the center of an object increases. It is shown in the equation below: [math]\displaystyle{ \v(r)={2pir/T}={omega}r }[/math]

File:Users/fergie/Desktop/angularvelocity.pngample.jpg

Point Particle System VS Extended System

Why is it useful to divide the kinetic energy into two different elements? When calculating the total energy of a system, depending on how it is modeled, it will contain one or more types of kinetic energies. Let's think about a system modeled as a point particle system. In this model of a system, we think of the object as one point, located at its center of mass. With this way of thinking, it becomes clear that there can only be one type of kinetic energy: translational kinetic energy. There cannot be any rotational kinetic energy because there are no atoms rotating about the center of mass, since we are thinking of the center of mass as the entire object. Our general energy equation thus boils down to this:

[math]\displaystyle{ \triangle E_{system} = W }[/math] where [math]\displaystyle{ W = F_{net} . \triangle r_{CM} }[/math] and [math]\displaystyle{ \triangle E_{system} = \triangle K_{translational} }[/math] since there is only translational kinetic energy.

We end up with [math]\displaystyle{ \triangle K_{translational} = F_{net} . \triangle r_{CM} }[/math]

Note: There may also be spring potential energy and rest energy depending on the example.

Therefore, viewing a system as a point particle system allows us to easily calculate the translational kinetic energy. This translational kinetic energy will be the same in the extended system.

After having calculated the translational kinetic energy of the system using the point particle system, we can use this value to calculate other terms in the general equation in the extended system.

We start with the general energy equation: [math]\displaystyle{ \triangle E_{system} = W }[/math] where [math]\displaystyle{ W = F_{net} . displacement }[/math]

In this extended system, we consider all the atoms and their rotation about the axis as well as the general movement of the center of mass. We end up with [math]\displaystyle{ \triangle K_{translational} + \triangle K_{rotational} + \triangle K_{vibrational} = F_{net} . displacement }[/math]

Note: Here again, there may be spring potential energy and rest energy included in this equation depending on the example.

A Computational Model

Vpython

There are not many applications of vpython for this chapter because it necessitates such a conceptual way of thinking. However, it is possible to make a program that calculates the rotational energy given displacements for each force and the magnitude of the force. The mass of the object and the initial conditions would have to be given as well.

Visualizing translational and rotational kinetic energy

It is important to really think about translational kinetic energy as the movement of the center of mass and only that. In the point particle system, only translational kinetic energy is present because we are visualizing the object only as its center of mass, and that is therefore the only kind of movement we have. Let's take the earth as an example. The earth rotates around itself, as well as around the sun. If you think of the earth only in terms of its center of mass, you realize that the center of mass only has one kind of movement: around the sun. It is useful to think of the earth in this case, the point particle system, as a dot, located at its center of mass.

In the extended system, however, we consider the movement of the center of mass as well as the movement of all the atoms around it. Since the atoms of the earth that are not its center rotate (one rotation every 24h), there is rotational energy. Its center of mass is still moving around the sun, there is therefore also translational energy. Here, we think of the earth as a sphere, not a dot, in which the atoms rotate about an axis or center.

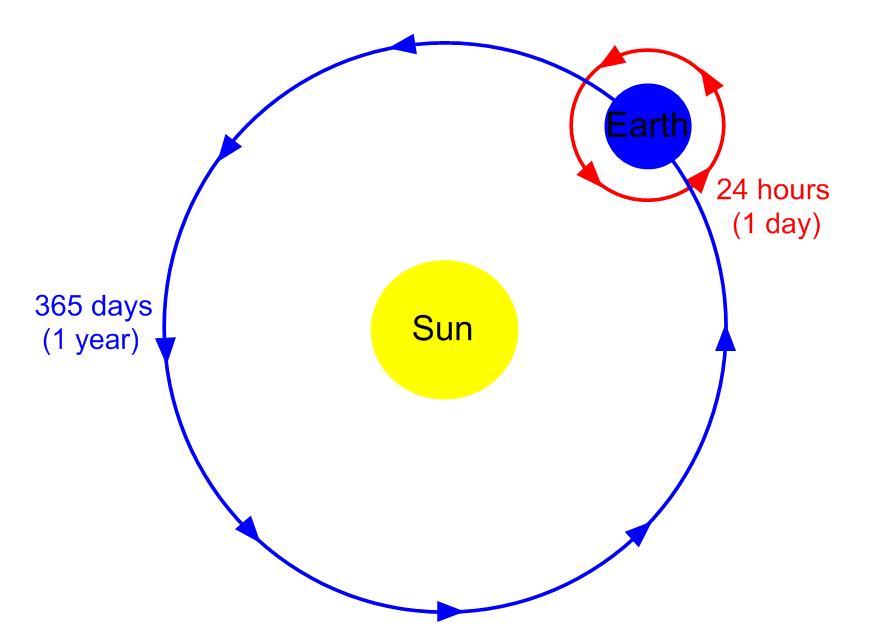
For another visual approach of this concept, you can watch the following video: https://www.youtube.com/watch?v=zDcf7eEaP0M.

Examples

Simple

Problem statement:

Calculate the rotational kinetic energy of a wheel of radius 100cm, mass 10kg, with and angular velocity of 22 radians/s.

Solution:

We know how to calculate the moment of inertia for a disk, and the moment of inertia for a wheel will be the same since all the atoms are at the same distance from the center. Therefore, [math]\displaystyle{ I = MR^2 = (10)(1)^2 = 10 kgm^2 }[/math]

From there, we can easily calculate the rotational kinetic energy: [math]\displaystyle{ K_{rotational} = \cfrac{1}{2}I\omega^2 = \cfrac{1}{2}(10)(22)^2 = 2420 }[/math] Joules

Middling

Problem statement:

A string is wrapped around a disk of radius 0.15m and mass 3kg. The disk is initially at rest, but you pull the string with a force of 10N along a smooth surface. The disk moves a distance d = 0.1m and your hand pulls through a distance h = 0.2m. What is the speed of the center of mass of the disk after having pulled the string?

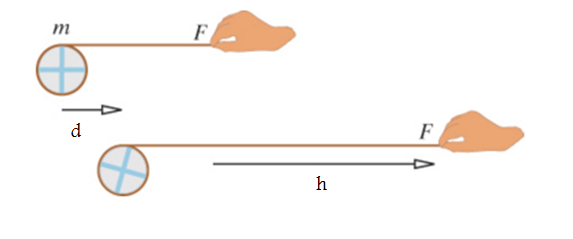
Solution:

The problem states that the disk is moving on a smooth surface, so there is no friction here. Since the problem asks about the speed of the center of mass, we will consider the point particle system first. We start with:

[math]\displaystyle{ \triangle K_{translational} = F_{net} . \triangle r_{CM} }[/math]

We know that the translational kinetic energy is [math]\displaystyle{ K = \cfrac{1}{2}mv_{CM}^2 }[/math]

So we end up with:

[math]\displaystyle{ \cfrac{1}{2}mv_{CM,f}^2 - \cfrac{1}{2}mv_{CM,i}^2 = F_{net} . \triangle r_{CM} }[/math]

Because initially the disk is still, we can reduce this equation to:

[math]\displaystyle{ \cfrac{1}{2}mv_{CM,f}^2 = F_{net} . \triangle r_{CM} }[/math]

[math]\displaystyle{ v_{CM,f}^2 = \cfrac{2. F_{net} . \triangle r_{CM}}{m} }[/math]

[math]\displaystyle{ v_{CM,f} = \sqrt{\cfrac{2. F_{net} . \triangle r_{CM}}{m}} }[/math]

[math]\displaystyle{ v_{CM,f} = \sqrt{\cfrac{ (2)(10)(0.1)}{3}} }[/math]

[math]\displaystyle{ v_{CM,f} = 0.816 }[/math] m/s

Difficult

Problem statement

A box contains a machinery that can rotate. The mass of the box and what it contains is 10kg. A string is wound around the machinery inside the box and comes out of a hole at the top of the box. Before you pull the string, the machinery is not rotating and the box is sitting still. You then pull 0.9m of string out of the box with a force F = 100N and the box lifts up a distance of 0.2m. What is the rotational Kinetic energy of the mechanism inside the box?

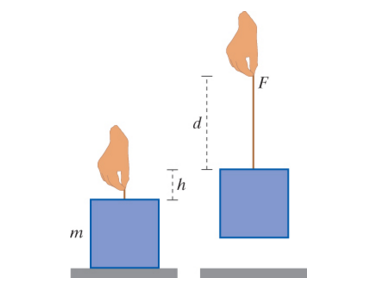
Solution

We cannot calculate the rotational energy directly because we do not have any indication of the shape of the mechanism and its angular speed. Therefore, we will use the point particle system and the extended system to find this value. Begin by finding the value of the translational kinetic energy of the system by using the point particle model. We have:

[math]\displaystyle{ \triangle K_{translational} = F_{net} . \triangle r_{CM} }[/math] [math]\displaystyle{ K_{translational,f} - K_{translational,i} = F_{net} . \triangle r_{CM} }[/math]

The initial translational kinetic energy is 0 because the center of mass of the object is not moving initially.

[math]\displaystyle{ K_{translational,f} = F_{net} . \triangle r_{CM} }[/math]

[math]\displaystyle{ K_{translational,f} = (F_{hand} - F_{grav}) (0.2) }[/math]

[math]\displaystyle{ K_{translational,f} = (114 - mg) (0.2) }[/math]

[math]\displaystyle{ K_{translational,f} = (114 - (10)(9.8)) (0.2) }[/math]

[math]\displaystyle{ K_{translational,f} = 3.2 }[/math] Joules

Now let's look at the extended system:

Here, we have:

[math]\displaystyle{ \triangle K_{translational} + \triangle K_{rotational} = F_{net} . displacement }[/math]

Since there is no initial translational or rotational kinetic energy, we get:

[math]\displaystyle{ K_{translational,f} + K_{rotational,f} = F_{net} . displacement }[/math]

[math]\displaystyle{ K_{rotational,f} = F_{net} . displacement - K_{translational} }[/math]

The gravitational force mg acts through the distance that the center of mass of the box moves, while the force of your hand acts through that distance plus the distance the string uncoils. Therefore, we have:

[math]\displaystyle{ K_{rotational,f} = (114)(0.2 + 0.9) - (10)(9.8)(0.2) - 3.2 }[/math]

[math]\displaystyle{ K_{rotational,f} = 102.6 }[/math] Joules

Connectedness

How is this topic connected to something that you are interested in?

In the book, this topic is very much related to sports. It uses countless examples from diving, ice skating or frisbee to demonstrate why kinetic energy can be separated into two terms. I have always been interested in sports and they were always a big part of my life. Therefore when I read the book, this was one of the most interesting sections to me because I felt some kind of connection to it, like it applied to my life, since I had ice-skated and dove when I was young.

1. How is it connected to your major?

Some biomedical engineers go on to work with sports stars on smart clothes or even prosthetics, in which case they have to deal with rotation and vibration, in addition to regular kinetic energy. The study of biomechanics largely relies on physics as well.

1. 1. Is there an interesting industrial application?

There are many developments of machines that will use kinetic energy for power. We may very well see a few years from now a shoe on the market that powers your cell phone or any other type of technology. There are many possibilities for advancements such as this one.

History

Kinetic energy was first set apart from potential energy by Aristotle. However, it wasn't until 1929 that Gaspard-Gustave Coriolis showed the first signs of understanding of kinetic energy the way that we do today. The term was later coined by William Thomson.

http://learning.alfriston.bucks.sch.uk/course/view.php?id=47

http://www.school-for-champions.com/astronomy/earth_motion.htm#.Vloe4HarSM8

Matter and Interactions By Ruth W. Chabay, Bruce A. Sherwood - Chapter 9

@@ Line 67: / Line 67: @@
 ===== Angular Speed =====
-The angular speed is a calculation of how fast the object is rotating. It can be calculated from the period, T, with the following formula : <math> \omega = \cfrac{2\pi}{T} </math>
+The angular speed is that rate at which the object is rotating. It is given in the following formula:
+<math> \omega = \cfrac{2\pi}{T} </math>]
-The rotational kinetic energy can thus be calculated using these two variables: <math> K_{rotational} = \cfrac{1}{2}I\omega^2 </math>.
+The angle which the disk turns is 2 pi in a time T. It is measured in units in radians per second. The tangential velocity of an object is related to some distance r and at the angular speed because the tangential velocity increases when the distance from the center of an object increases. It is shown in the equation below:
+<math> \v(r)={2pir/T}={omega}r</math>
+[[File:Users/fergie/Desktop/angularvelocity.pngample.jpg]]
 ==== Point Particle System VS Extended System ====