Superposition Principle

The Superposition Principle states that the net result of multiple vectors acting on a given place and time is equal to the vector sum of each individual vector. For intro physics, this mostly relates to effect that multiple electric or magnetic fields and forces have on a certain location. Claimed by Jvotaw3 (talk) Claimed by jnmng3 (Fall 2017)

A Mathematical Model

The Superposition Principle is derived from the properities of additivity and homogeneity for linear systems which are defined in terms of a scalar value of a by the following equations:

[math]\displaystyle{ F(x_1 + x_2) = F(x_1) + F(x_2)\quad Additivity }[/math]

[math]\displaystyle{ aF(x) = F(ax)\quad Homogeneity }[/math]

The principle can be applied to any linear system and can be used to find the net result of functions, vectors, vector fields, etc. For the topic of introductory physics, it will mainly apply to vectors and vector fields such as electric forces and fields.

If given a number of vectors passing through a certain point, the resultant vector is given by simply adding all the the vectors at that point. For example, for a number of uniform electric fields passing though a single point, the resulting electric field at that point is given by

[math]\displaystyle{ \vec{E} = \vec{E}_{1} + \vec{E}_{2} +...+ \vec{E}_{n} = \sum_{i=1}^n\vec{E}_{i} }[/math]

and this same concept can be applied to electric forces as well as to magnetic fields and forces. This is more useful when dealing with the effect that multiple point charges have on each other is an area of void of other electric fields. The resultant electric field for at a point for a system of point charges is given by

[math]\displaystyle{ \vec{E} = \frac{1}{4 \pi \epsilon_0}\sum_{i=1}^n\frac{q_i}{r_i^2}\hat{r_i} }[/math]

This approach can be applied to any other sources of electric or magnetic field or force by simply adding together the each of the vectors at a specific point

Examples

When attempting to solve these problems be sure to show all steps in your solution and include diagrams whenever possible.

Simple - Two Point Charges and One Dimension

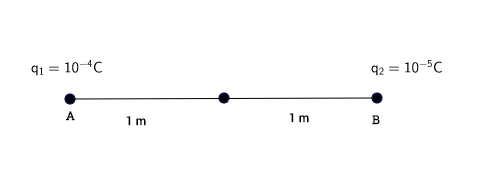If [math]\displaystyle{ Q_1 }[/math] equals 1e-4 C and [math]\displaystyle{ Q_2 }[/math] equals 1e-5C, what is the net electric field at the midpoint of both charges?

Click for Solution

Medium - Two Point Charges and Two Dimensions

If [math]\displaystyle{ Q_1 }[/math] and [math]\displaystyle{ Q_2 }[/math] are positive point charges with a charge of e, what is the net electric field at point P?

Click for Solution

To begin this problem, the first step is to find [math]\displaystyle{ r_1 }[/math] [math]\displaystyle{ r_2 }[/math], the vectors from the charges to point P as well as their magnitudes:

[math]\displaystyle{ \vec{r_1} = 3\hat{i}+2\hat{j}-(0\hat{i}+0\hat{j})\Rightarrow\vec{r_1} = 3\hat{i}+2\hat{j} }[/math]

[math]\displaystyle{ ||\vec{r_1}|| = \sqrt{3^2 + 2^2} =\sqrt{13} }[/math]

[math]\displaystyle{ \vec{r_2} = 3\hat{i}+2\hat{j}-(4\hat{i}+0\hat{j})\Rightarrow\vec{r_2} = -1\hat{i}+2\hat{j} }[/math]

[math]\displaystyle{ ||\vec{r_2}|| = \sqrt{-1^2 + 2^2} =\sqrt{5} }[/math]

Using these in the equation for an electric field from a point charge, you get:

[math]\displaystyle{ \vec{E_1} = \frac{1}{4 \pi \epsilon_0}\frac{Q_1}{||r_1||^2}\hat{r_1}=\frac{1}{4 \pi \epsilon_0}\frac{e}{13}\lt \frac{3}{\sqrt{13}}\hat{i}+\frac{2}{\sqrt{13}}\hat{j}\gt = \lt 9.21E-11\hat{i}+6.14E-11\hat{j}\gt }[/math]N/C

[math]\displaystyle{ \vec{E_2} = \frac{1}{4 \pi \epsilon_0}\frac{Q_2}{||r_2||^2}\hat{r_2}=\frac{1}{4 \pi \epsilon_0}\frac{e}{5}\lt \frac{-1}{\sqrt{5}}\hat{i}+\frac{2}{\sqrt{5}}\hat{j}\gt = \lt -1.29E-10\hat{i}+2.58E-10\hat{j}\gt }[/math]N/C

Then, simply add the two electric fields together:

[math]\displaystyle{ \vec{E}=\vec{E_1}+\vec{E_2} = \lt -3.69E-11\hat{i}+3.19E-10\hat{j}\gt }[/math]

Difficult - Five Point Charges and Three Dimensions

If all point charges have a charge of e, what the the net electric field present at point L?

Click for Solution

This problem is similar to the previous example but the now includes the z axis and more points. Since there are 5 points, we'll only focus on one, but work through the whole problem. Again, first each vector and magnitude:

[math]\displaystyle{ \vec{d_5} = 0\hat{i}+0\hat{j}+0\hat{k}-(2\hat{i}-1\hat{j}-1\hat{k})-\Rightarrow\vec{d_5} = -2\hat{i}+1\hat{j}+1\hat{k} }[/math]

[math]\displaystyle{ ||\vec{d_5}|| = \sqrt{(-2)^2 + 1^2 + 1^2} = 2 }[/math]

Do the same for each of the other point charges and plug them into the electric field formula:

[math]\displaystyle{ \vec{E_5} = \frac{1}{4 \pi \epsilon_0}\frac{Q_5}{||d_5||^2}\hat{d_5}=\frac{1}{4 \pi \epsilon_0}\frac{e}{4}\lt \frac{-2}{2}\hat{i}+\frac{1}{2}\hat{j}+\frac{1}{2}\hat{k}\gt = \lt -3.6E-10\hat{i}+1.8E-10\hat{j}+1.8E-10\hat{k}\gt }[/math]N/C

Doing the same steps for the other electric fields and add them all together:

[math]\displaystyle{ \vec{E_1} = \lt 1.44E-9\hat{i}+0\hat{j}+0\hat{k}\gt }[/math]N/C

[math]\displaystyle{ \vec{E_2} = \lt 0\hat{i}-1.44E-9\hat{j}+0\hat{k}\gt }[/math]N/C

[math]\displaystyle{ \vec{E_3} = \lt -1.29E-10\hat{i}+0\hat{j}+2.58E-10\hat{k}\gt }[/math]N/C

[math]\displaystyle{ \vec{E_4} = \lt 0\hat{i}+0\hat{j}-1.44E-9\hat{k}\gt }[/math]N/C

[math]\displaystyle{ \vec{E} = \vec{E_1}+\vec{E_2}+\vec{E_3}+\vec{E_4}+\vec{E_5}=\lt 9.51E-10\hat{i}-1.26E-9\hat{j}+1.00E-9\hat{k}\gt }[/math]N/C

History

Daniel Bernoulli

The superposition principle was supposedly first stated by Daniel Bernoulli, a famous scientist known for his work in fluid mechanics, statistics, and the Bernoulli Principle. In 1753, he stated that, "The general motion of a vibrating system is given by a superposition of its proper vibrations." This idea was at first rejected by some other popular scientists until it became widely accepted due to the work of Joseph Fourier, a famous scientist known for his work on the Fourier Series, which is used in heat transfer and vibrations, as well as his discovery of the Greenhouse Effect.

See also

• Electric Field
  • Point Charge
  • Electric Dipole
• Electric Force
• Magnetic Field
• Magnetic Force

Further reading

Books, Articles or other print media on this topic

http://www.acoustics.salford.ac.uk/feschools/waves/super.php

References

[1] [2] [3] [4]