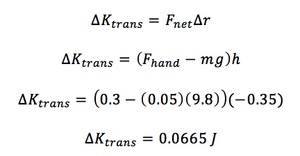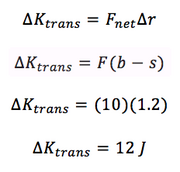Point Particle Systems

Claimed by Diana Sweeney

The Main Idea

The point particle system is a way of measuring energy change. It greatly simplifies the system of interest down to a single point, oftentimes doing this by looking at the center of mass of a system. This can also greatly simplify a problem, as in a multi particle system it can be difficult to determine what exactly the surroundings are. A point particle system puts the system at one specific place, then everything else is in the surroundings. Thus, the only energy change focused on is the change in kinetic energy, particularly translational kinetic energy. Translational kinetic energy is the energy that comes from an object moving from one location to another. The extended system, or real system, looks at energy changes within a system as well. Using both of these systems together can help pinpoint specific energy transfers.

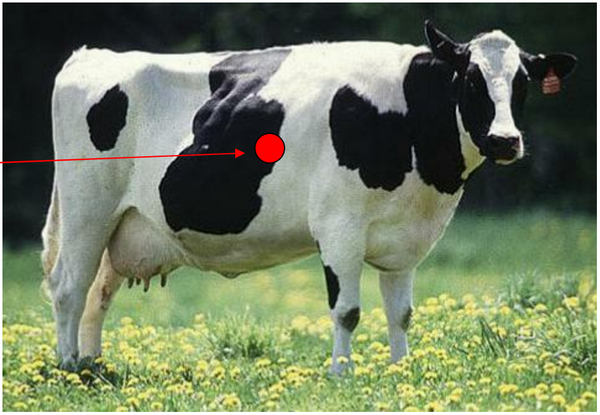Center of Mass of a Cow as a Point

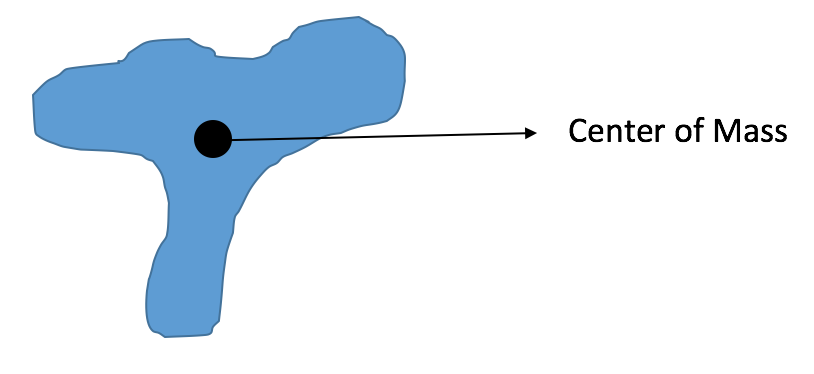
A Mathematical Model

Translational kinetic energy is equal to 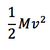, where M is the total mass of the system and v is the velocity of the center of mass.

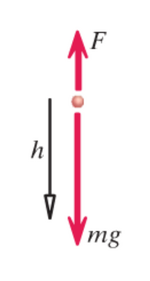
The change in translational kinetic energy is equal to , where F is the net force acting on the object and delta r is the change in position of the object center of mass.

In a point particle system, where delta K is change in translational kinetic energy. This is why the change in translational energy can be written as the net force times the change in distance of the center of mass. Remember, there is no change in internal energy.

Another explanation of this is that in the point particle system, total change in energy is equal to the total change in kinetic energy, because there is no change in internal energy. Because of the energy principle, , where delta E is change in total energy and W is work, the change in translational kinetic energy is thus also equal to work, which is equal to as well, given by the energy principle.

Examples

Jumper Model

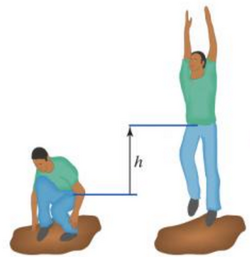
A person jumps straight up in the air from a crouching position. Their center of mass moves h, or 2 m. Their total mass, m is equal to 60 kg. Find the velocity of the center of mass of the jumper. When the jumper jumps, the normal force of the ground is equal to 2x the force of gravity.

To make this problem simpler, use the center of mass of the person to collapse the whole system to one point.

Imagine the jumper's center of mass as a point, and it moves up 2 m.

Remember, , and . We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore,

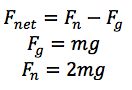
Steps:

Notice that the initial translational kinetic energy is 0, as the person is initially at rest. When worked out, the v = 6.26 m/s.

The final translational kinetic energy can be used for further calculations if one was to calculate the total change in energy of the real system. These calculations would allow you to find the change in various forms of internal energy, such as heat energy or chemical energy.

---

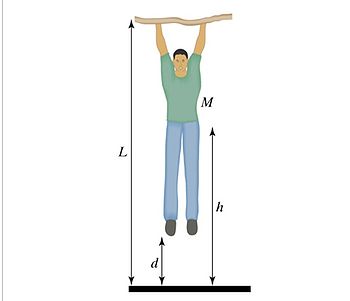
Another example that the point particle system can be applied to is someone hanging motion-less and then jumping down into a crouch position.

Looking at the system as a point particle system, you can look at the initial and final states of the man in order to find the change in energy. We are going to again use a formula for work,

In order to find the speed just before your feet touch the ground, you can set an equation as the following:

The equation for the point particle system ∆E= ∆K=Work can be applied in order to find different variables asked for in a problem.

Remember that if the man does not move, then the work done by the man will be 0 joules, because there is no displacement.

Yo-Yo Example

You pull up on a string the distance d, 0.2 m, with a force, F, 0.3 N. The yo-yo falls a distance h, 0.35 m. The mass of the yo-yo, m, is 0.05 kg. What is the change in translational kinetic energy?

For this example, the Fnet is equal to the force of your hand and the gravitational force of the earth. Delta r is equal to the movement of the yo-yo down, h.

Steps:

This information could be used to solve for the extended system, which would include the work done by your hand and the earth, as well as rotational kinetic energy.

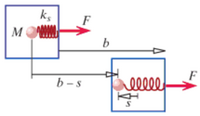
Spring in a Box Example

Suppose a thin box contains a ball of clay with the mass M, 2 kg, connected to a relaxed spring, with a stiffness ks, 1.2. The masses of the box and the spring are negligible. It is initally at rest, and then a constant force of F, or 10 N. The box moves a distance b, 1.5 m, and the spring stretches a distance s, 0.3 m, so that the clay sticks to the box. What is the translational kinetic energy of the box?

For the point particle system, the center of mass is the clay because the other masses are negligible. Therefore, delta r is equal to b-s, or 1.2 m. The only force acting on is F in the +x direction.

Steps:

This information could then be used for the extended system. In this example, the extended system would also include the work done by the force F, the potential energy of the spring,as well as any other internal energies.

Connectedness

1. How is this topic connected to something that you are interested in?

I think it is interesting how physicists have simplified the process of finding changes of energy in a system in order to make approximations and calculate more complicated changes in energy. For me, it really helped me to understand exactly what translational kinetic energy is and how it applies to the entire system.

1. How is it connected to your major?

My major is industrial engineering, and although I do not think this topic applies directly to my major, it applies to simplifying and making a more efficient and easy way to calculate the changes of energy in a system. Finding the most efficient way to do something is one of the main goals of industrial engineering, and so in that way, I really enjoy this method of finding changes in energy.

See also

Further reading

For more help, a helpful page is: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real

A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y

External links

See also Real Systems for further information on using Point Particle Systems to solve for the Real Systems.

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.

Yo-yo Clipart: https://www.clipartbest.com