Conductivity: Difference between revisions
No edit summary |
|||
| Line 151: | Line 151: | ||
[http://hyperphysics.phy-astr.gsu.edu/hbase/electric/resis.html HyperPhysics Explanations] | [http://hyperphysics.phy-astr.gsu.edu/hbase/electric/resis.html HyperPhysics Explanations] | ||
[https://en.wikipedia.org/wiki/Portal:Physics|Physics Portal] | |||
===External links=== | ===External links=== | ||
Revision as of 17:48, 29 November 2017
Claimed by Patrick Todd (Spring 2017) Claimed by Anthony Chawki (Fall 2017)
Definition
Conductivity is the degree to which a specified material conducts electricity, calculated as the ratio of the current density in the material to the electric field that causes the flow of current. (It is the reciprocal of the resistivity.)
In other words, Conductivity is the measure of the ease at which an electric charge or heat can pass through a material. Electrical conductivity tells us how well a material will allow electricity to travel through it. Thermal conductivity tells us the ease upon which thermal energy (heat for most purposes) can move through a material.
Symbols
Electrical Conductivity is measured in siemens per meter and is often represented using the Greek letters σ (lowercase sigma), κ (kappa), or γ (lowercase gamma).
SI Units
Conductivity's SI units is the siemens per metre, [math]\displaystyle{ A^{2} s^{3} m^{−3} kg^{−1} }[/math](named after Werner von Siemens) or, more simply, [math]\displaystyle{ S m^{−1} }[/math].
Classification of Materials by Conductivity
Conductors, Semiconductors, and Insulators are the main three classifications of a material when talking about its electrical conductivity. Conductors are materials with high conductivity. Semiconductors have an in between level of conductivity, while insulators have low conductivity. Meaning if you want to pass a lot of electricity to something use a conductor, if you want to pass some electricity but also lower the original amount use a semiconductor, and if you want to cut the flow of electricity use an insulator. Provided below is a list of materials that fit into each category.
Conductors: Gold, Iron, Silver, Copper, Aluminum, Tin
Semiconductors: Silicon, Germanium
Insulators: Glass, Porcelain, Rubber, Cloth, Paper, Air




Conductivity By Material Type
Metals
Conductivity in metals decreases when temperature is increased. When the temperature increases, the resistance of the metal also increases linearly. As the temperature of a metal is reduced, the temperature dependence of resistivity follows a power law function of temperature.
The structure of metal is made up of a lattice of atoms. The outer shell of electrons that surround the parent atoms can come free and travel throughout the lattice, also known as an positive ionic lattice. A simpler definition of this phenomenon is the "sea" of electrons. This "sea" of electrons can move throughout the metal structure and conduct an electrical current. The electric field created by the electric potential cause the electrons to move to the positive terminal. The electrons are packed so densely that the electromagnetic field can travel at the speed of light with each electron having a small drift velocity.
The resistance in metals are created by temperature, the cross sectional area, the length, and the speed of vibration of the crystal lattice. The more resistance that is present the less conductive the metal is. The temperature causes irregularities in the lattice. If the cross sectional area is bigger then there is more electrons per unit length are available to carry current. Therefore, the smaller the cross sectional area the more resistance in the wire. The longer the wire the more likely scattering events take place. The more scattering events the higher the resistance in the wire. Impurities in the metal increase resistance too. The different ions in the metal create irregularities, which in turn create a vibration in the metal.
Semiconductors
Semiconductors are materials that have a conductivity in-between that of an insulator and a conductor. Their electrical resistance are much higher than ordinary conductors but still much lower than most insulators. Interestingly enough, their resistance decreases as their temperature increases, which is behavior opposite to that of a metal (insulator).
Temperature Dependence
Conductivity of a material is determined by two factors: the concentration of free carriers available to conduct current and their mobility (or freedom to move). In a semiconductor, both mobility and carrier concentration are temperature dependent. As temperature increases, the electrical resistivity of metals increases. This is a reason why when computers heat up, they tend to slow down. Some materials exhibit superconductivity at extremely low temperatures. Below a certain temperature, resistivity vanishes, such as Pb (Lead) at 7.20 K.
Plasma
Plasma is a very good electrical conductor. Its electric potential is a special potential called plasma or space potential. It exists in the space between charged particles. If an electrode was put inside the plasma the potential would drop a considerable amount compared to the plasma potential because of a phenomenon called Debye sheath. The high conductivity results in relatively small electric fields.
Superconductors

Lowering the temperature of a metallic conductor will decrease the electrical resistance. The metal can be cooled gradually until the resistance is almost zero. Once the temperature drops past the critical temperature the resistance drops to zero. The zero resistance can allow the metal to have electrical current flow in a loop indefinitely without a power source.
Applications of a Superconductor
- Magnetic Resonance Imaging (MRI) and Nuclear Magnetic Resonance (NMR)
- Particle Accelerators and Magnetic Fusion Devices
- Electric Motors and Generators
- Supermagnets
- Digital Devices
Band Theory
Equations
Conductivity Relationship to Resistivity
[math]\displaystyle{ σ=1/ρ }[/math]
σ= Conductivity
ρ= Electric Resistivity
Maxwell's Equation for Electric Conductivity
[math]\displaystyle{ J=σE }[/math]
J= Electric Current Density
E= Electric Field
σ= Conductivity
Electric current density can be thought of as the electric current per cross sectional area of a specific material. Therefore this formula relates to each material differently. Every material has a specific conductivity associated with it, and this conductivity can help describe the electric field in each material. For example, materials such as copper and silver have extremely high electric conductivity and therefore in order to not have an almost infinite electric current density we can approximate the electric field inside the metals to be zero. This equation is essentially the proof for all metals having a zero electric field on the inside. The relationship between these three variables is known as Ohm's Law.
Poulliet's Law of Resistivity
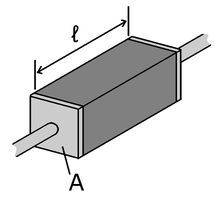
[math]\displaystyle{ R=ρℓ/A }[/math]
R = Electric Resistance
ρ = Electric Resistivity
ℓ = Length
A = Cross-Sectional Area
Poulliet's Law states that a given material's resistance will increase in length, while it will decrease with an increase in Area. The SI unit for this law is Ohm*meter. The electrical resistivity is different for every substance.
Conductivity in Real Life
Conductors are used to carry electricity, as well as electrical signals in circuits. Complementary metal–oxide–semiconductors, or CMOS for short, are the foundational building block of gate based logic circuits, that make up the majority of all modern electronics. CMOS circuits are composed of a combination of p-type and n-type semiconductors. These semiconductors will change their conductivity, based on the applied voltage, allowing for logic of 0's and 1's, or low voltage and high voltage, to be transferred through logical circuits. This allows us to apply boolean logic to circuits, such as AND and OR logic, or even create an amalgamation of AND's and OR's to create electronics, such as multiplexors, switches, latches, registers, decoders, encoders, etc.
Fun Examples
Salt Water Conductivity Experiment
Mathematical Problems
Simple
Find the Conductivity of a material with an electrical field of [math]\displaystyle{ 5*10^{12} (E = 5*10^{12}) }[/math] and a current density of [math]\displaystyle{ 5*10^2 (J = 5*10^2) }[/math].
| Answer |
|---|
| [math]\displaystyle{ =10^{10} }[/math] |
Medium
Find the Resistivity of a wire with the resistance of [math]\displaystyle{ 0.69Ω*m (R=0.69Ω*m) }[/math], length of [math]\displaystyle{ 10m (ℓ=10m) }[/math], and cross-sectional area of [math]\displaystyle{ 100m^{2} (A=100m^{2}) }[/math].
| Answer |
|---|
| 690 = 10ρ |
| ρ = 69 |
History
Stephen Gray, Father of Conduction
Born 1666 in Canterbury, England. Died 1736 in London, England.
Gray was an innovative thinker who performed many a experiment including work with the transmission of electricity. One day while performing one of his experiments, unbeknownst to him he discovered the difference between insulators and conductors. He was working with transmitting electricity and he changed the transmission wire from silk to brass wire when he noticed that electricity passes completely different in brass than it does in silk. After said discovery, Gray spend the next 3 years with the help of friends and family doing more research in similar topics, and with this research some might say solidified his name as the father of conduction.
Claude Pouillet, Pouillet's Law
Born February 16, 1720 in Cusance, France. Died June 14, 1868 in Paris, France.
Claude was one of the earliest scientists to examine the Sun's influence on Earth's atmosphere, beyond simple radiation. After approximating the solar constant to be 1228 [math]\displaystyle{ W/m^{2} }[/math], which turned out to be extremely close to the now recognized constant of 1367 [math]\displaystyle{ W/m^{2} }[/math]. This success earned him a chair in the Physics department at the École Normale Supérieure. From there he went on to design and create early, operational versions of sine and tangent galvanometers which measure current (more commonly known as an ammeter).