Parallel Circuits: Difference between revisions
No edit summary |
No edit summary |
||
| Line 22: | Line 22: | ||
A schematic is the easiest way to visualize a parallel circuit, and circuits in general. | A schematic is the easiest way to visualize a parallel circuit, and circuits in general. | ||
[[ | [[Image:pc3.png]] | ||
The circuit above contains a battery and three resistors. Notice R1, R2, and R3 occupy different branches of the circuit. They are connected by only two nodes, one at the top of the circuit and one at the bottom, even though it may seem like there are four nodes in the schematic. | The circuit above contains a battery and three resistors. Notice R1, R2, and R3 occupy different branches of the circuit. They are connected by only two nodes, one at the top of the circuit and one at the bottom, even though it may seem like there are four nodes in the schematic. | ||
| Line 38: | Line 38: | ||
'''Calculate the total resistance of this parallel circuit.''' | '''Calculate the total resistance of this parallel circuit.''' | ||
[[Image:pc3.png]] | |||
[[ | |||
| Line 47: | Line 46: | ||
:::<math>\frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}</math> | :::<math>\frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}</math> | ||
In this case, we simply need to substitute the values of <math>R_1</math>, <math>R_2</math>, and <math>R_3</math> into the formula, and solve for <math>R_{total}</math>. | In this case, we simply need to substitute the values of <math>R_1</math>, <math>R_2</math>, and <math>R_3</math> into the formula, and solve for <math>R_{total}</math>. | ||
| Line 57: | Line 57: | ||
===Middling=== | ===Middling=== | ||
'''Calculate the current | '''Calculate the total current of the following circuit.''' | ||
[[Image:pc4.png]] | |||
===Solution=== | ===Solution=== | ||
Start by finding the total resistance of the circuit. | |||
:::<math>\frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}</math> | |||
:::<math>\frac{1}{R}_{total}=\frac{1}{75Ω}+\frac{1}{150Ω}+\frac{1}{25Ω}+\frac{1}{100Ω}</math> | |||
:::<math>{R}_{total}=14.286Ω</math> | |||
From here, we can use Ohm's Law to find the total current <math>I_{total}</math> | |||
:::<math>I=\frac{V}{R}</math> | |||
:::<math>I_{total}=\frac{V}{R_{total}}</math> | |||
:::<math>I_{total}=\frac{9V}{14.286Ω}</math> | |||
:::<math>I_{total}=0.63A</math> | |||
This problem can be solved in one step by combining Ohm's Law with what we know about the resistance of a parallel circuit (see [[A Mathematical Model]] above) | |||
===Difficult=== | ===Difficult=== | ||
'''Calculate the current running through <math>R_2 </math>.''' | '''Calculate the current running through <math>R_2 </math>.''' | ||
Revision as of 18:51, 29 November 2017
Claimed by Alex Oshin (Fall 2017)
The Main Idea

Components of a circuit can be connected in two main ways, in series or in parallel. This page focuses on components connected in parallel, which means that the components are connected such that the same voltage is applied to each component. A parallel circuit is a circuit that is connected entirely in parallel. Each component in a parallel circuit occupies its own branch, or path in the circuit, and these branches are connected at locations called nodes. Thus a charge passing through the circuit has multiple possible paths that it can take when it reaches a node. This property is the reason why adding an additional resistor in a parallel circuit results in a decreased total resistance of the circuit (since there is an additional path that the charges can follow). Likewise, if a path is removed, or if the circuit is broken in a single path, more charge is forced to flow through the remaining paths, and the total resistance increases.
A Mathematical Model
Ohm's Law is essential for understanding circuits, and in particular, the relationship between current, voltage, and resistance.
- [math]\displaystyle{ I=\frac{V}{R} }[/math]
The voltage is the same for all elements of a parallel circuit.
- [math]\displaystyle{ V_{total}=V_1=V_2=...=V_n }[/math]
The total resistance of a parallel circuit is the reciprocal of the sum of the reciprocals of the individual resistances.
- [math]\displaystyle{ \frac{1}{R_{total}}=\frac{1}{R_1}+\frac{1}{R_2}+...+\frac{1}{R_n} }[/math]
Applying Ohm's Law to these two equations, we can find the total current of the circuit.
- [math]\displaystyle{ I_{total}=V(\frac{1}{R_{1}}+\frac{1}{R_{2}}+...+\frac{1}{R_{n}}) }[/math]
And the current flowing through a component with resistance [math]\displaystyle{ R_{i} }[/math] will be:
- [math]\displaystyle{ I_{i}=\frac{V}{R_{i}} }[/math]
These results are consistent with Kirchhoff's circuit laws, and can be similarly derived.
A Computational Model
A schematic is the easiest way to visualize a parallel circuit, and circuits in general.
The circuit above contains a battery and three resistors. Notice R1, R2, and R3 occupy different branches of the circuit. They are connected by only two nodes, one at the top of the circuit and one at the bottom, even though it may seem like there are four nodes in the schematic.
The following image shows a real-world example.
Each lightbulb acts like a resistor in the previous circuit schematic.
Examples
Simple
Calculate the total resistance of this parallel circuit.
Solution
Start by applying the formula for the resistance of a parallel circuit.
- [math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} }[/math]
In this case, we simply need to substitute the values of [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_2 }[/math], and [math]\displaystyle{ R_3 }[/math] into the formula, and solve for [math]\displaystyle{ R_{total} }[/math].
- [math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{50Ω}+\frac{1}{70Ω}+\frac{1}{100Ω} }[/math]
- [math]\displaystyle{ {R}_{total}=22.581Ω }[/math]
Middling
Calculate the total current of the following circuit.
Solution
Start by finding the total resistance of the circuit.
- [math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4} }[/math]
- [math]\displaystyle{ \frac{1}{R}_{total}=\frac{1}{75Ω}+\frac{1}{150Ω}+\frac{1}{25Ω}+\frac{1}{100Ω} }[/math]
- [math]\displaystyle{ {R}_{total}=14.286Ω }[/math]
From here, we can use Ohm's Law to find the total current [math]\displaystyle{ I_{total} }[/math]
- [math]\displaystyle{ I=\frac{V}{R} }[/math]
- [math]\displaystyle{ I_{total}=\frac{V}{R_{total}} }[/math]
- [math]\displaystyle{ I_{total}=\frac{9V}{14.286Ω} }[/math]
- [math]\displaystyle{ I_{total}=0.63A }[/math]
This problem can be solved in one step by combining Ohm's Law with what we know about the resistance of a parallel circuit (see A Mathematical Model above)
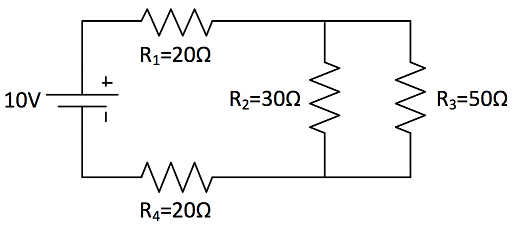
Difficult
Calculate the current running through [math]\displaystyle{ R_2 }[/math].
Solution
First we have to find out the total resistance of this circuit. Since we have both series and parallel component in the circuit, we have to add all the components to find out the total resistance.
- [math]\displaystyle{ R_{Parallel}=\frac{R_2R_3}{R_2+R_3}=18.75 Ω }[/math]
- [math]\displaystyle{ R_{Total}=R_1+R_{Parallel}+R_4=58.75 Ω }[/math]
Now using the Ohm's law we could determine the total current running through the circuit.
- [math]\displaystyle{ V_{Total}=I_{Total}R_{Total} }[/math]
- [math]\displaystyle{ V_{Total}=10V }[/math]
- [math]\displaystyle{ I_{Total}=\frac{V_{Total}}{R_{Total}} }[/math]
- [math]\displaystyle{ I_{Total}=0.17A }[/math]
We can now use the current divider law to calculate the current running through [math]\displaystyle{ R_2 }[/math].
- [math]\displaystyle{ I_2=I_{Total}\frac{R_{Parallel}}{R_2}=0.10625A }[/math]
To check our answer, calculate the current running through [math]\displaystyle{ R_3 }[/math]
- [math]\displaystyle{ I_3=I_{Total}\frac{R_{Parallel}}{R_3}=0.06375A }[/math]
- [math]\displaystyle{ I_{Total}=I_2+I_3=0.17A }[/math]
Since the total current in a parallel circuit equals to the sum of the current running through each branch, we could verify our answers.
Connectedness
Circuit, including parallel, series, RC, RL... , could be applied to many areas. Circuits are used for many the power sources in the world. In every day's life we encounter using electrical events from turning on lights, using a mp3 player, and so on. Majoring in computer engineering, I have to deal with many circuits, and apply it to the real world. I choose this topic to cover more details about the circuit, and since a lot of students had hard time solving the circuit problem in Test 3. I'm interested in this area, because I can really understand what I can't easily visualize it in real life. By studying circuit, I can understand how power or electricity works, and even computer! In detail, I'm interested in the application of a simple circuit to design a computer. How integrated circuits are used to build a hardware and software.
This website provides some very useful video that shows how simple circuits works in the real world.
History
Integrated Circuit was invented by two inventors name Jack Kilby, and Robert Noyce in the mid 1950s. The work was not done in a corporation. They just came up with the same idea in the same time. Jack Kilby was working for Texas Instrument, whereas Robery Noyce was an research engineer who founded for Semiconductor Corporation. To design a complex computer machine, they needed something more small with more data, and information compared to original transistors, resistors, and capacitors. So they designed an integrated circuit that has many functions within a single chip. It was used to deal with complex matters with minimum cost. From the start of 1960s, many company started to use a chip, replacing the original transistors, and resistors. This integrated circuit is known as one of the most important invention in human kind. I wanted to introduce this specific circuit, because this is what I'm really interested in in my area computer engineering. (Designing the core of the computer)
See also
You could refer to other topics where you can build more idea about the circuits.
First, you should know clearly about the series circuit in order to understand the basic circuit design. In real life we could see a parallel circuit combined with the series circuit, as the example shown in before.
When we thoroughly understand the general idea of a circuit, it's very useful to refer to more complicated circuit as RC cirucit.
These pages would provide some basic information that we could refer to help understand the concept of parallel circuit
Further reading
Introduction to Electric Circuits 9th edition James A. Svoboda Richard C. Dorf
Basic Electric Circuit Theory Issaak D. Mayegoyz W.Lawson
Matter & Interactions Vol. II: Electric and Magnetic Interactions, 4th Edition R. Chabay B Sherwood
External links
References
Including the 3 textbook, I have refereed to the following external sources to create a wikipage.