Rotational Kinematics: Difference between revisions
AdityaKunta (talk | contribs) |
AdityaKunta (talk | contribs) |
||
| Line 40: | Line 40: | ||
===A Computational Model=== | ===A Computational Model=== | ||
As shown in this Earth- spacecraft model, [http://www.glowscript.org/#/user/akuntamukkula/folder/Private/program/Lab06/edit], rotation can be modeled through VPython and other computer languages. | |||
from __future__ import division | |||
from visual import * | |||
from visual.graph import * #Invoke graphing routines | |||
scene.y = 400 #Move orbit window below graph | |||
scene.width =1024 | |||
scene.height = 760 | |||
#CONSTANTS | |||
G = 6.7e-11 | |||
mEarth = 6e24 | |||
mMoon = 0 | |||
mcraft = 15000 | |||
deltat = 5000 | |||
pscale = 0.5 | |||
fscale = 30000 | |||
dpscale = .5 | |||
#OBJECTS AND INITIAL VALUES | |||
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan) | |||
Moon = sphere(pos = vector(4e8,0,0), radius = 1.75e6, color = color.white) | |||
scene.range=11*Earth.radius | |||
parr = arrow(color=color.green) | |||
farr = arrow(color = color.cyan) | |||
dparr = arrow(color = color.red) | |||
Fnet_tangent_arrow = arrow(color = color.yellow) | |||
Fnet_perp_arrow = arrow(color = color.magenta) | |||
# Choose an exaggeratedly large radius for the | |||
# space craft so that you can see it! | |||
craft = sphere(pos=vector(-71680000,-3008000,0),radius = Earth.radius/3, color=color.yellow) | |||
vcraft = vector(0,sqrt((G * mEarth)/(mag(craft.pos - Earth.pos))),0) | |||
pcraft = mcraft*vcraft | |||
vMoon = vector(0,sqrt((G * mEarth)/(mag(Moon.pos - Earth.pos))),0) | |||
trail1 = curve(color=craft.color) ## craft trail: starts with no points | |||
trail2 = curve(color=Moon.color) | |||
t = 0 | |||
scene.autoscale = 0 ## do not allow camera to zoom in or out | |||
momentum_Moon = mMoon * vMoon | |||
#CALCULATIONS | |||
print("p=",pcraft) | |||
while t < 200000: #time of model: | |||
rate(10) ## slow down motion to make animation look nicer | |||
## you must add statements for the iterative update of | |||
## gravitational force, momentum, and position | |||
R1 = craft.pos - Earth.pos | |||
R2 = craft.pos - Moon.pos | |||
Rmag1 = mag(R1) | |||
Rmag2 = mag(R2) | |||
Rhat1 = norm(R1) | |||
Rhat2 = norm(R2) | |||
Fmag1 = (G*(mEarth)*(mcraft))/(Rmag1**2) | |||
Fmag2 = (G*(mMoon)*(mcraft))/(Rmag2**2) | |||
Fnet1 = -Fmag1 * Rhat1 | |||
Fnet2 = -Fmag2 * Rhat2 | |||
Fnet = Fnet1 + Fnet2 | |||
vcraft = vcraft + (Fnet*deltat)/mcraft | |||
p_initial = pcraft | |||
pcraft = pcraft + Fnet*deltat | |||
p_final = pcraft | |||
craft.pos = craft.pos + vcraft*deltat | |||
parr.pos = craft.pos | |||
farr.pos = craft.pos | |||
parr.axis = pcraft * pscale | |||
farr.axis = Fnet * fscale | |||
pcraft_i = pcraft + vector(0,0,0) | |||
deltap = pcraft - pcraft_i | |||
dparr.pos = craft.pos | |||
dparr.axis = Fnet * fscale | |||
Fnet_tangent = ((mag(p_final) - mag(p_initial))/deltat) * norm(pcraft) | |||
Fnet_tangent_arrow.pos = craft.pos | |||
Fnet_tangent_arrow.axis = Fnet_tangent * 90000 | |||
Fnet_perp = Fnet - Fnet_tangent | |||
Fnet_perp_arrow.pos = craft.pos | |||
Fnet_perp_arrow.axis = Fnet_perp * 10000 | |||
scene.center = craft.pos | |||
scene.range = craft.radius * 60 | |||
## check to see if the spacecraft has crashed on the Earth. | |||
## if so, get out of the calculation loop | |||
if Rmag1 < Earth.radius: | |||
break | |||
if Rmag2 < Moon.radius: | |||
break | |||
trail1.append(pos=craft.pos) ## this adds the new position of the spacecraft to the trail | |||
trail2.append(pos = Moon.pos) | |||
t = t+deltat | |||
print("Fnet=",Fnet) | |||
print('Calculations finished after ',t,'seconds') | |||
print("craft.pos=",craft.pos) | |||
print("vcraft=",vcraft) | |||
print("F_perp=",Fnet_perp) | |||
==Examples== | ==Examples== | ||
Revision as of 23:45, 29 November 2017
Claimed by Aditya Kuntamukkula 2017
The Main Idea
Rotational motion is defined as an object moving around an axis in contrast to translational motion which involves the object moving in a straight trajectory.
A Mathematical Model
Rotation can be characterized by its angular velocity and angular acceleration. The equations are listed below.
Angular velocity:
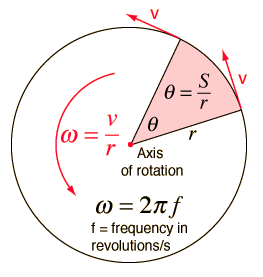
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{v}}{\boldsymbol{r}} }[/math] ,
where [math]\displaystyle{ {\boldsymbol{v}} }[/math] is the velocity of the object and [math]\displaystyle{ {\boldsymbol{r}} }[/math] is the radius of the circle of motion. It can also be represented as the change in angle over the distance traveled in the formula shown below:
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{d\theta}}{\boldsymbol{dt}} }[/math] , where [math]\displaystyle{ {\boldsymbol{d\theta}} }[/math] is the change in angle and [math]\displaystyle{ {\boldsymbol{dt}} }[/math] is the change in time.
Angular acceleration is equal to alpha:
- [math]\displaystyle{ \boldsymbol{{\alpha}} = \frac{\boldsymbol{a_t}}{\boldsymbol{r}} }[/math] ,
where [math]\displaystyle{ {\boldsymbol{a_t}} }[/math] is the tangential acceleration of the object and [math]\displaystyle{ {\boldsymbol{r}} }[/math] is the radius of the circle of motion.
Rotational Kinetic Energy:
An object with a center of mass at rest can still have rotational kinetic energy. For example, if a disk is suspended in the air and spun, it has no translational kinetic energy. The position of the disk does not change. However, since it is spinning (rotating), it still has kinetic energy. To account for this, we can relate angular velocity with the moment of inertia of the object to find a value for the rotational kinetic energy.
Rotational Kinetic Energy:
- [math]\displaystyle{ {KE}_{rot} = \frac{{1}}{{2}}{I}_{cm}{ω^2} }[/math]
Relation to Work and Energy Principle:
The energy principle states:
- [math]\displaystyle{ {E}_{f} = {E}_{i} + W }[/math]
We can apply the energy principle to rotational kinetic energy as well to find changes in kinetic energy and work done on the system.
A Computational Model
As shown in this Earth- spacecraft model, [1], rotation can be modeled through VPython and other computer languages.
from __future__ import division from visual import * from visual.graph import * #Invoke graphing routines scene.y = 400 #Move orbit window below graph
scene.width =1024 scene.height = 760
- CONSTANTS
G = 6.7e-11 mEarth = 6e24 mMoon = 0 mcraft = 15000 deltat = 5000 pscale = 0.5 fscale = 30000 dpscale = .5
- OBJECTS AND INITIAL VALUES
Earth = sphere(pos=vector(0,0,0), radius=6.4e6, color=color.cyan) Moon = sphere(pos = vector(4e8,0,0), radius = 1.75e6, color = color.white) scene.range=11*Earth.radius parr = arrow(color=color.green) farr = arrow(color = color.cyan) dparr = arrow(color = color.red) Fnet_tangent_arrow = arrow(color = color.yellow) Fnet_perp_arrow = arrow(color = color.magenta)
- Choose an exaggeratedly large radius for the
- space craft so that you can see it!
craft = sphere(pos=vector(-71680000,-3008000,0),radius = Earth.radius/3, color=color.yellow) vcraft = vector(0,sqrt((G * mEarth)/(mag(craft.pos - Earth.pos))),0) pcraft = mcraft*vcraft vMoon = vector(0,sqrt((G * mEarth)/(mag(Moon.pos - Earth.pos))),0) trail1 = curve(color=craft.color) ## craft trail: starts with no points trail2 = curve(color=Moon.color) t = 0 scene.autoscale = 0 ## do not allow camera to zoom in or out momentum_Moon = mMoon * vMoon
- CALCULATIONS
print("p=",pcraft) while t < 200000: #time of model:
rate(10) ## slow down motion to make animation look nicer ## you must add statements for the iterative update of ## gravitational force, momentum, and position R1 = craft.pos - Earth.pos R2 = craft.pos - Moon.pos Rmag1 = mag(R1) Rmag2 = mag(R2) Rhat1 = norm(R1) Rhat2 = norm(R2) Fmag1 = (G*(mEarth)*(mcraft))/(Rmag1**2) Fmag2 = (G*(mMoon)*(mcraft))/(Rmag2**2) Fnet1 = -Fmag1 * Rhat1 Fnet2 = -Fmag2 * Rhat2 Fnet = Fnet1 + Fnet2 vcraft = vcraft + (Fnet*deltat)/mcraft p_initial = pcraft pcraft = pcraft + Fnet*deltat p_final = pcraft craft.pos = craft.pos + vcraft*deltat parr.pos = craft.pos farr.pos = craft.pos parr.axis = pcraft * pscale farr.axis = Fnet * fscale pcraft_i = pcraft + vector(0,0,0) deltap = pcraft - pcraft_i dparr.pos = craft.pos dparr.axis = Fnet * fscale
Fnet_tangent = ((mag(p_final) - mag(p_initial))/deltat) * norm(pcraft) Fnet_tangent_arrow.pos = craft.pos Fnet_tangent_arrow.axis = Fnet_tangent * 90000
Fnet_perp = Fnet - Fnet_tangent Fnet_perp_arrow.pos = craft.pos Fnet_perp_arrow.axis = Fnet_perp * 10000
scene.center = craft.pos scene.range = craft.radius * 60
## check to see if the spacecraft has crashed on the Earth. ## if so, get out of the calculation loop
if Rmag1 < Earth.radius:
break
if Rmag2 < Moon.radius:
break
trail1.append(pos=craft.pos) ## this adds the new position of the spacecraft to the trail trail2.append(pos = Moon.pos) t = t+deltat
print("Fnet=",Fnet) print('Calculations finished after ',t,'seconds') print("craft.pos=",craft.pos) print("vcraft=",vcraft) print("F_perp=",Fnet_perp)
Examples
Simple
A simple example and application of the concept of rotation is the earth's rotation on it's axis. It rotates once every 24 hours. What is the angular velocity?
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{d\theta}}{\boldsymbol{dt}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\delta\theta}}{\boldsymbol{\delta t}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{2\pi}}{\boldsymbol{24}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{12}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{12}}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}*\frac{\boldsymbol{1}}{\boldsymbol{3600}}\frac{\boldsymbol{hr}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{\pi}}{\boldsymbol{43200}}\frac{\boldsymbol{rad}}{\boldsymbol{s}} }[/math]
Angular velocity can also be represented as change in angle (theta) over change in time. In this case, the earth rotates 2pi radians in 24 hours which reduces to pi/12 rad/hr and that is the equivalent of pi/43200 rad/s.
Medium
A cylinder with a 2.5 ft radius is rotating at 120 rpm. Find the angular velocity in rad/sec. Find the linear velocity of a point on its rim in mph.
- [math]\displaystyle{ \boldsymbol{{w}} = {\boldsymbol{120}}\frac{\boldsymbol{rev}}{\boldsymbol{min}}*\frac{\boldsymbol{2\pi}}{\boldsymbol{1}}\frac{\boldsymbol{rad}}{\boldsymbol{rev}}*\frac{\boldsymbol{1}}{\boldsymbol{60}}\frac{\boldsymbol{min}}{\boldsymbol{s}} = {\boldsymbol{4\pi}}\frac{\boldsymbol{rad}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{w}}{\boldsymbol{r}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{4\pi}}\frac{\boldsymbol{rad}}{\boldsymbol{s}}*{\boldsymbol{2.5}}\frac{\boldsymbol{ft}}{\boldsymbol{rad}} = {\boldsymbol{10\pi}}\frac{\boldsymbol{ft}}{\boldsymbol{s}} }[/math]
- [math]\displaystyle{ \boldsymbol{{v}} = {\boldsymbol{10\pi}}\frac{\boldsymbol{ft}}{\boldsymbol{s}}*\frac{\boldsymbol{3600}}{\boldsymbol{1}}\frac{\boldsymbol{s}}{\boldsymbol{hr}}*\frac{\boldsymbol{1}}{\boldsymbol{5280}}\frac{\boldsymbol{miles}}{\boldsymbol{ft}} =\frac{\boldsymbol{75\pi}}{\boldsymbol{11}}\frac{\boldsymbol{miles}}{\boldsymbol{hr}} }[/math]
To find the solution of this problem, rpm (revolutions per minute) should be converted to radians/second. Following this, the linear velocity can be calculated by using the v=wr formula shown above. The angular velocity is 4pi radians per second and the linear velocity is 75pi/11 or 21.42 mph.
Difficult
A tire with a 9 inch radius is rotating at 30 mph. Find the angular velocity at a point on its rim. Also express the result in revolutions per minute.
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{v}}{\boldsymbol{r}} }[/math]
- [math]\displaystyle{ \boldsymbol{{r}} = {\boldsymbol{9}}{\boldsymbol{in}}*\frac{\boldsymbol{1}}{\boldsymbol{12}}\frac{\boldsymbol{ft}}{\boldsymbol{in}}*\frac{\boldsymbol{1}}{\boldsymbol{5280}}\frac{\boldsymbol{miles}}{\boldsymbol{ft}} = \frac{\boldsymbol{1}}{\boldsymbol{7040}}{\boldsymbol{miles}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \frac{\boldsymbol{30}}{\frac{\boldsymbol{1}}{\boldsymbol{7040}}}\frac{\frac{\boldsymbol{miles}}{\boldsymbol{hr}}}{\frac{\boldsymbol{rad}}{\boldsymbol{miles}}} = \boldsymbol{{211200}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}} }[/math]
- [math]\displaystyle{ \boldsymbol{{w}} = \boldsymbol{{211200}\frac{\boldsymbol{rad}}{\boldsymbol{hr}}}*\frac{\boldsymbol{1}}{\boldsymbol{2\pi}}\frac{\boldsymbol{rev}}{\boldsymbol{rad}}*\frac{\boldsymbol{1}}{\boldsymbol{60}}\frac{\boldsymbol{hr}}{\boldsymbol{min}} = \frac{\boldsymbol{1760}}{\boldsymbol{\pi}}\frac{\boldsymbol{rev}}{\boldsymbol{min}} }[/math]
Connectedness
Rotation is an extremely important aspect of dynamics (the study of moving objects) which plays a big role in biomechanics. Rotation relates to several important body parts such as the shoulder where there are two axis of rotation, the medial-lateral axis and the anterior-posterior axis. A study of the movement of the shoulder helps to treat medical conditions that may affect this area. Dynamics is also very important in many other disciples, including mechanical engineering and aerospace engineering.
See also
To learn more about Rotation in a more complete context, please refer to Torque or Rigid-Body Objects or Angular Momentum.
Further reading
Books, Articles or other print media on this topic
External links
Some other resources to further understand rotation are the following:
http://www.mathwarehouse.com/transformations/rotations-in-math.php
http://demonstrations.wolfram.com/Understanding3DRotation/
References
[1] Biomechanics, Basic. “It Is Important When Learning about (n.d.): n. pag. Web.
[2] "Angular Velocity and Angular Acceleration." Van Nostrand's Scientific Encyclopedia (2005): n. pag. Web