SI Units

This page is about SI Units. This page is created by Jinyoung Lee. Improved by Ryan Yeung. Claimed by Deepti Veludhandi 2017.

Claimed by Ian Bolger (Spring 2018), Improved by Ian Bolger (Spring 2018)

The Main Idea

SI unit stands for the 'International System of Units'. It is the modern form of the metric system, and is the most widely used system of measurement. It is used among almost all of the larger countries, with the major exception being the United States. It is used whenever scientific observations or measurements are made. It is made up of 7 standard units derived from constants of nature. It justifies twenty-two named units, and includes many more unnamed coherent derived units. The system also establishes a set of twenty prefixes to the unit names and unit symbols that may be used when specifying multiples and fractions of the units. This internationally recognized system of units is adopted and used in measurement in a diverse set of fields. The system is still evolving though. As precision and technology improve, the system changes based on international decisions and agreement. The last unit to be added was in 1999. More units and derivations are foreseen as time goes on.

A Mathematical Model

There are some mathematical operations required to translate a non-SI unit to SI unit. These are generally simple operations such as addition, subtraction, division, and multiplication. For example [math]\displaystyle{ {\frac{lb}{2.2}} = kg }[/math] Since 1 kg(SI unit) is equal to 2.2 lb, to change lb to SI unit, or kg, lb has to be divided by 2.2.

Another example can be length. [math]\displaystyle{ {\frac{inch}{0.394}} = cm }[/math] Same method used to change lb to kg. Since 1cm is equal to 0.394inch, inch has to be divided by 0.394 to become SI unit, cm.

These transformations can be done throughout all of the recorded units in the world. In order to preform these simply find the accepted transformation values, and preform a simple division or multiplication operation.

Computational Model

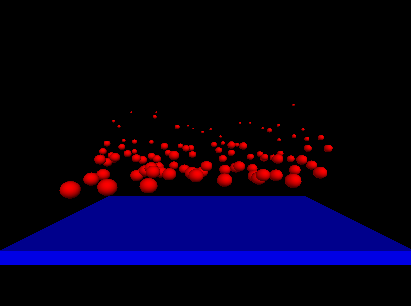
Think of SI Units as an underlying base foundation consisting of numerous derivations to encompass numerous other units to apply to an immense amount of situations. Here is a VPython simulation intricately depicting this mental image of a base with hundreds of other derivations on top.

This computational model perfectly depicts the overarching concept of SI Units and the international system used to create a wide set of units used in calculations across numerous different curriculum and facets.

Base SI units

This image above shows the base SI units. These units include length, mass, time, electric current, temperature, substance amount, and light intensity. There also exist a variety of other units that are not as commonplace as these other 7. The base SI Units are the metre (m), kilogram (kg), second (s), ampere (A), kelvin (K), mole (mol), candela (cd). These are the building blocks of the system unto which the derived units come from. The derived units are formed by powers, products, and quotients of the base units. Combinations of base and derived units sum to even further derived units.

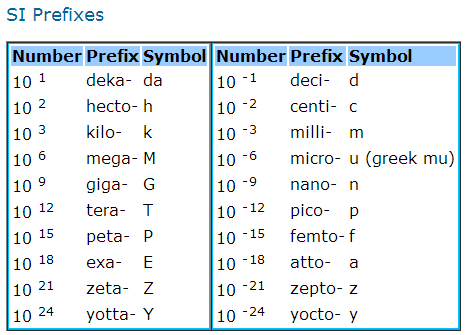
Prefixes

Mass, length or any numbers in physics can be very small or very large. Electrons can be a great example. The mass of electron is 0.0000000000000000000000910938356g or 9.10938356 E-31. In SI, prefixes are available to adjust the size of a unit so as to keep the number of those units reasonable. It is kind of difficult to read that number in word. However with the prefix it can be. Image below shows the list of prefixes.

These prefixes are incredibly useful for clarity purposes. The prefixes listed are incredibly useful for a speaker or writer in order to help ease their use.

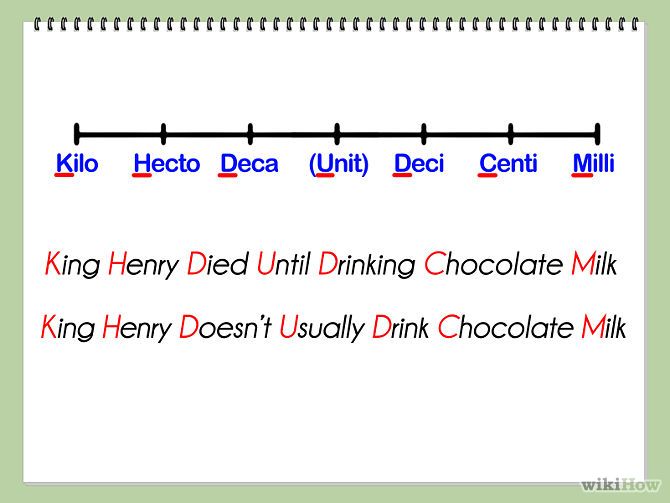
Here is a video that helps to explain the prefixes and an easy way to remember:

Easy Way to Memorize Metric Prefixes

Derived SI units

This image above shows the relationships between many units used in physics based on base SI units. As we can see, most of the units in physics is related to the SI units. It is because there are many quantities that cannot be expressed by a single base SI unit. For example, when talking about the density, it is volume/mass. Mass has it's own SI unit which is a gram. However volume doesn't. Volume is expressed with derived SI unit, meters cubed. As a result, unit for density is [math]\displaystyle{ \mathrm{m}^3/\mathrm{g} }[/math] . Those units are called derived SI units. Units can be combined to create new unit. Some frequently-used combinations have their units named. Here are some examples:

• Watt (W), the unit of power.
  • [math]\displaystyle{ \mathrm{W} = \mathrm{J}/\mathrm{s} \ }[/math]

• Pascal (Pa), the unit of pressure.
  • [math]\displaystyle{ \mathrm{Pa} = \mathrm{N}/\mathrm{m}^2 \ }[/math]

• Hertz (Hz), the unit of frequency.
  • [math]\displaystyle{ \mathrm{Hz} = 1/\mathrm{s} = \mathrm{s}^{-1} \ }[/math]

• Newton (N), the unit of force.
  • [math]\displaystyle{ \mathrm{N} = \mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2 }[/math]

• Joule (J), the unit of energy.
  • [math]\displaystyle{ \mathrm{J} = \mathrm{N} \cdot \mathrm{m} = \mathrm{kg} \cdot \mathrm{m}^2/\mathrm{s}^2 }[/math]

• Coulomb (C), the unit of electric charge.
  • [math]\displaystyle{ \mathrm{C} = \mathrm{A} \cdot \mathrm{s} }[/math]

• Volt (V), the unit of electric potential or voltage.
  • [math]\displaystyle{ \mathrm{V} = \mathrm{J}/\mathrm{C} = \mathrm{W}/\mathrm{A} \ }[/math]

The list is incredibly useful for measuring quantities that do not have a standard SI unit already in place. These calculations are used frequently to find further derived SI Units in complex equations.

Examples of Calculations Using SI Units

Connectedness

This topic can be applied to every aspect of science. When solving the problem, or even when doing research, every equation and theory is based on SI units. It is a promise between scientists that they will use these certain units to reduce errors or misunderstanding. Therefore, it is very important to know the concept of SI units. This topic is connected to not only physics but also every other scientific subject. In addition, it might not be familiar in the United States, but in most other countries, they use SI units in ordinary life. SI units create a form of standardization throughout the scientific community. This standardization stems from their connection to fundamental constants. These constants are dependent on naturally occurring laws on Earth. As a result, since these units are connected to these constants that are unchanging no matter what location on Earth they're being observed at, this system of measurement is able to achieve a high level of standardization. This establishes a sense of unity and allows scientists to be on the same page no matter what nationality they are. It's through the use of these units by the community of scientists as a whole that error can be reduced to a minimum and calculations and findings can be standardized across the globe. SI units also allow scientists to reproduce experiments and record their results in the same form. This allows for more credibility among findings as well. SI units are also very useful for the use of dimensional analysis. Dimensional analysis is the mathematical problem solving method that essentially means that any number expression can be multiplied by another and its inherent value won't be changed. This vital problem solving idea is possible due to the fact that SI units can be converted to non SI units with incredible ease. SI units create an incredible amount of standardization throughout the scientific community and have been essential for the production of viable and credible scientific results.

Due to recent events in the scientific community and the new levels of accuracy achieved from the use of modern and scientifically advanced equipment, there have been several discoveries that can redefine how we understand fundamental constants. Since SI units are closely intertwined with fundamental constants, these discoveries have great relevance. Most of these discoveries are in the field of quantum physics which is a new field in comparison to other scientific subjects. The technology age has given scientists cutting-edge equipment allowing them to reach results that are more specific and accurate than ever before. For example, this equipment can allow them to calculate a more accurate mass of an electron, which is an important constant and affects the values of base units in the SI unit system. When discoveries like these directly affect our understanding of fundamental constants, they can have an effect on the SI unit system. However, some discoveries, but not all, might only change the value of a constant by a minuscule amount, so the SI units will barely change their values and will most likely not directly affect the way most students solve problems since they will tend to round in problems.

History

The Metric System was created around the time of the French Revolution and the subsequent deposition of two platinum standards representing the meter and the kilogram, on 22 June 1799, in the Archives de la Republic in Paris can be seen as the first step in the development of the present International System of Units. Each of the base units has root within the physical world. For example the unit of metre is derived from dimensions of the Earth, the kilogram was derived the volume of of one liter of water. These 2 units are the baseline for the remainder of the SI system. The new metric system was originally abandoned by France. In 1837, the metric system was readopted by France, and slowly then became adopted by the scientific community. After this a man named James Clerk Maxwell presented the idea of a number of base units, time, mass, and length. This 3 base units could then be used to derive a series of other measurements throughout the scientific world. However it was quickly discovered that these units cannot describe non-mechanical properties. Most importantly they couldn't properly describe the electrical properties of the world. A man named Giovanni Giorgi, an Italian physicist and electrical engineer, proposed a fourth base unit should be added to the original 3 in order to properly describe the electrical systems of the world. This unit was later decided, in 1935, to be the ampere thus allowing the world to aptly describe electrical systems as well. As the years passed these units began to become more and more commonplace among the world, with many other countries beginning to use the SI system as their main form of measurement. The SI system quickly became the accepted scientific measuring system as well. The use of this system has helped to advance and drive scientific advancement throughout the years.

Furthermore, the SI unit system was established in 1960 by the 11th General Conference on Weights and Measures. The CGPM is the international authority that ensures wide spread of the SI system, and it modifies the SI system as necessary to reflect the latest advances in science and technology. The General Conference receives the report of the International Committee for Weights and Measures on work accomplished. It discusses and examines the arrangements required to improve the International System of Units (SI). It also then endorses the results of new fundamental determinations and various scientific resolutions and applies them to an international scope. It further decides all major issues concerning the development of the organization as a whole.

Further reading

SI Units for Clinical Measurement 1st Edition by Donald S. Young

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

Base units of the SI, fundamental constants and modern quantum physics by Christian J Bordé

References and External Links

http://physics.nist.gov/ National institute of standards and Technology.

http://wps.prenhall.com/wps/media/objects/165/169061/blb9ch0104.html Pearson educational site.

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

Tutorial & Drill Problems for General Chemistry (and Intro) By Walter S. Hamilton, Ph.D.

Base units of the SI, fundamental constants and modern quantum physics By Christian J Bordé, Published 15 September 2005

https://www.youtube.com/embed/h04x3Vr2GGE