Potential Difference in a non-Uniform Field

Dalton Lewis Fall 2018

Main Idea

Fields

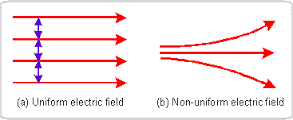
Uniform Field: If the magnitude and direction of an electric field at each and every point in a region is the same, the field in that region is uniform. More specifically, if the electric field vector doesn't vary with position. Non-Uniform Field: If the magnitude and direction of an electric field is different at some point in the region, the field in that region is considered non-uniform.

Electric Field Models: When looking at the graphs below, the Uniform Field has parallel and equal magnitude arrows throughout the region whereas the Non-Uniform Field will have points that go other directions at some point.

Potential Difference

Potential difference is the change in electric potential between a final and initial location. The work done on the charge during this movement will alter its potential energy and because of this change in potential energy, there is a difference in electric potential between these locations.

When considering Potential Difference calculated in non-Uniform Fields, the regions should be split into smaller sections of Uniform Fields. For example, the path from the initial location to the final location passes through two regions of uniform, but different fields. In this case, you would split this into two separate calculations for each region and then combine to determine the total potential difference

Mathematical Model

[math]\displaystyle{ \Delta V }[/math] = [-([math]\displaystyle{ E1_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E1_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E1_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math])] + [-([math]\displaystyle{ E2_{x} }[/math]●[math]\displaystyle{ \Delta x }[/math] + [math]\displaystyle{ E2_{y} }[/math]●[math]\displaystyle{ \Delta y }[/math] + [math]\displaystyle{ E2_{z} }[/math]●[math]\displaystyle{ \Delta z }[/math]] + ... = -[math]\displaystyle{ \Sigma \vec{E} }[/math]●[math]\displaystyle{ \Delta \vec{l} }[/math]

Examples

Calculating Potential Difference from A to B- in a non-Uniform Field

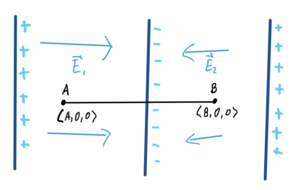
For this problem, you will need to split the path into two separate parts.

Create a point in between the boundaries of the two Electric Fields, and use this point to calculate the individual potential differences. -Calculate from A to the center -Calculate from the center to B The final step is adding the potential differences for both to get A to B

See also

External links

https://www.youtube.com/watch?v=j2k6LDafXHI

https://www.youtube.com/watch?v=LG2t1_acgik

https://www.youtube.com/watch?v=qki3pTacXBE

https://www.youtube.com/watch?v=vj2zLThvf-c