Friction

This page describes several types of friction and explains how they affect systems.

The Main Idea

Friction is a force that resists movement between surfaces in contact. It is caused by the interactions between the molecules that make up objects. There are three types of friction: Static Friction, which resists motion between surfaces that are not moving with respect to each other; Kinetic Friction, which resists motion between surfaces that are moving with respect to each other; and fluid friction, which resists the motion of bodies moving through gases and liquids. When objects or substances touch, their surfaces of contact are not perfectly smooth on the molecular scale. The irregularities on these surfaces are ultimately responsible for all types of friction. All types of friction depend on the materials comprising the surfaces of the objects and substances involved, as well as on the normal force they exert on each other (that is, the force with which they are pressed together).

1. Static Friction
When two objects touch each other and there is no sliding between their surfaces of contact, they exert static friction forces on each other. The static friction force acting on each object opposes any force that would cause it to slide relative to the other object. For example, consider a heavy dresser at rest on the floor. If a child pushes against the side of the dresser in an attempt to slide it, that exerts a force on the dresser, but the ground would exert on it an equal and opposite static friction force that balances the force of the child. The static friction force can take on whatever direction and magnitude necessary to balance an external net force that threatens to cause sliding motion between two surfaces. However, the static friction force is limited by the maximum magnitude it can exert. If the external force becomes strong enough, the static friction force can be overcome and the surfaces can begin to slide. For example, now consider an adult pushing against the same heavy dresser. The adult can exert a stronger force than the child, and if it exceeds the maximum possible static friction force, the dresser can be set into motion and slid across the floor. At this point the friction force between the dresser and the floor becomes kinetic. Static friction is a result of the interlocking of rough surfaces. The protrusions on one surface settle into the grooves on the other when they are pressed together, and overcoming the interlocking requires a force strong enough to either break the protrusions or slide them past each other.
2. Kinetic Friction
When two objects touch each other and there is sliding between their surfaces of contact, they exert a kinetic friction force on each other. The kinetic friction force acting on each object has a constant magnitude and acts in a direction opposite to its direction of motion relative to the other object. If the kinetic friction force is the only force acting on each object, they will eventually come to rest relative to each other, at which point the friction force between them becomes static. For example, consider a crate sliding across the floor. It will slow down and eventually come to rest due to the kinetic friction force between it and the floor, unless another force acts on it, such as the pushing of a person that wants to keep the crate moving. Kinetic friction force lowers the kinetic energy of a system, converting it to Thermal Energy. In other words, sliding between surfaces causes the surfaces to heat up. Usually in mechanical physics, this thermal energy is no longer considered part of the system and is considered lost because it usually dissipates into the environment without ever being converted back into mechanical energy. Kinetic friction is the result of abrasion between the protrusions of rough surfaces. The protrusions hit each other, sometimes causing them to break and always causing the molecules comprising them to wiggle. This increases the kinetic energy of the molecules at the sliding surfaces and reduces the kinetic energy of the macroscopic objects. This molecular energy is thermal energy.
3. Fluid friction
When an object moves through a liquid or gas, the fluid exerts a force on the object in the direction opposite to its motion relative to the fluid. Air Resistance is one common example of fluid friction that can affect the motion of projectiles and other objects in the earth's atmosphere. In many problems, you are asked to assume that the effects of air resistance are negligible because it is often not as strong as other forces and can significantly complicate math. However, the force exerted on an object by air resistance can be significant depending on the mass and geometry of the object, and it is beneficial to understand fluid friction for other fluids, such as water, as well.

Temperatures of interacting surfaces rise because of such interactions. Generally, friction makes it harder to move objects. There are two main types of friction that are covered in Physics 2211: Static Friction and Kinetic Friction. Static friction can be described as the friction acting on resting objects. Kinetic friction is the friction acting on objects in motion.

Frictional forces depend on a few factors: the normal force and the coefficient of friction.

In simple terms, the normal force [math]\displaystyle{ {F}_{N} }[/math] or [math]\displaystyle{ {N} }[/math] is the equivalent force between objects. For example, when an object of mass M is placed on a table, there is a gravitational force Mg on the table. If the table can support the object without collapsing, the table exerts an equivalent force Mg on the object. According to the momentum principle, since there is no change in momentum, the net force must be 0. This is also apparent since there is no movement if the table can support the object.

[math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}\Delta{t} = 0 }[/math]

OR

[math]\displaystyle{ {F}_{g} = {M}{g} }[/math]

[math]\displaystyle{ {N} = {M}{g} }[/math]

[math]\displaystyle{ {F}_{net} = {F}_{g} - {N} = {0} }[/math]

The coefficient of friction is usually specific to each object or material. The coefficient of static friction is denoted by [math]\displaystyle{ {μ}_{s} }[/math] and the coefficient of kinetic friction is denoted by [math]\displaystyle{ {μ}_{k} }[/math]

Static Friction:

[math]\displaystyle{ {F}_{s} \le {μ}_{s}{N} }[/math]

Static friction is the frictional force that must be overcome to begin moving an object at rest. The static friction can be no more than the normal force multiplied by the coefficient of static friction. Therefore, the maximum static friction an object can have is [math]\displaystyle{ {μ}_{s}{N} }[/math].

Kinetic Friction:

[math]\displaystyle{ {F}_{k} = {μ}_{k}{N} }[/math]

Kinetic friction is the frictional force that exists between objects already at motion. It acts to oppose the movement of an object. Kinetic friction can be observed, for example, when a soccer ball is kicked across a field. The friction between the ball and the field will eventually bring the ball to a stop.

Interestingly, friction is also required for rolling motion. Without friction, objects would not be able to roll. This is true because friction results in torque acting on the object, causing the rolling motion. An example of this can be seen in cars that are stuck in a ditch or similar situations. If there is not enough friction between the car's wheels and the ground, the car's wheels will simply spin in place, and the car will not move.

A Mathematical Model

As stated above:

Static Friction:

[math]\displaystyle{ {F}_{s} \le {μ}_{s}{N} }[/math]

Kinetic Friction:

[math]\displaystyle{ {F}_{k} = {μ}_{k}{N} }[/math]

When attempting to solve problems relating to friction, one possible method of approach is to consider the net force acting on an object. If there is a force [math]\displaystyle{ {F} }[/math] pushing an object to the right, and a frictional force [math]\displaystyle{ {F}_{f} }[/math] opposing the movement, then the net force is [math]\displaystyle{ {F}_{net} = {F} - {F}_{f} }[/math].

Another possible approach is by using the momentum principle [math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} }[/math]. The momentum principle can help solve problems where you need to account for time, net force, or change in momentum.

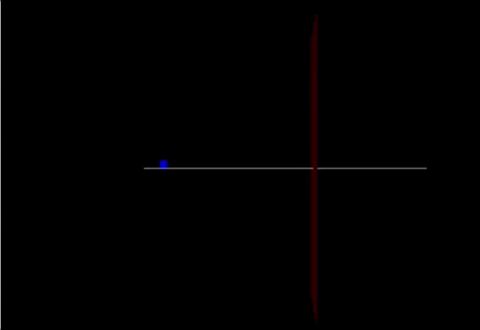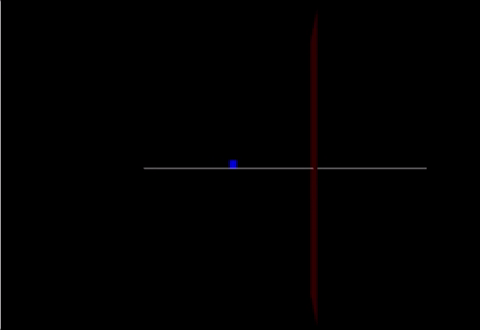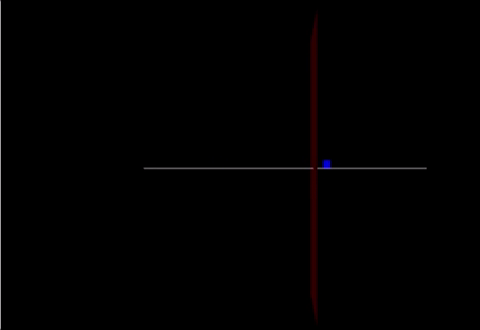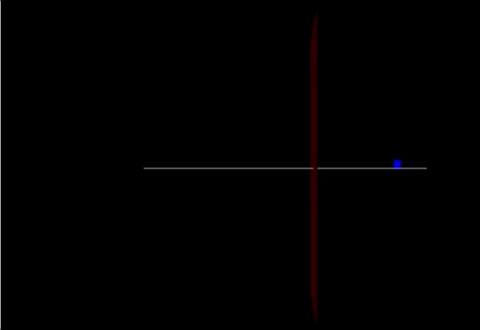
A Computational Model

Link: https://trinket.io/glowscript/76028c1809

Code:

def friction():
   from __future__ import division
   from visual import *
   from visual.graph import *

   mcart = 100
   mew = vector(2.9,0,0)

   track =  box(pos=vector(0,-0.05,0), size=vector(20.0,0.05,0.10), color=color.white)
   cart =  box(pos=vector(-10,0.25,0), size=vector(.5,0.6,0.03), color=color.blue)
   marker = box(pos = vector(2,0,0), size = vector(0,20,5), color = color.red)

   cart.v=vector(2.4,0,0)
   cart.p = mcart*cart.v
   F = vector(90,0,0)
   F2 = vector(-200,0,0)
   F3 = (mcart * mew)
   print(F3)

   deltat = 0.01
   t = 0

   while t < 5.02:

       if cart.pos.x < 2:
           cart.v = cart.p / cart.m
           Fnet = F
           cart.p = cart.p + Fnet*deltat
           cart.pos = cart.pos + (cart.p/mcart)*deltat

       else:
           
           cart.v = cart.p / cart.m
           Fnet = F-F3
           cart.p = cart.p + Fnet*deltat
           cart.pos = cart.pos + (cart.p/mcart)*deltat
           
       t = t + deltat
       rate(100)
       
   print(cart.pos)
   
friction()

Conceptualizing Friction

Why Friction Exists

It's important to understand why friction exists. Imagine a brick laying at rest on a table as seen below:

Now, if we take a look at the brick on a molecular level rather than a macroscopic scale, we can see that electron repulsion between the brick's molecules and the ground keeps the brick on the surface of the ground so that the brick doesn't simply "sink" into the ground. Electron repulsion one of the primary reasons why surfaces in contact interact with each other. Because however, there is a force due to gravity on the brick, the electrons in the ground also must exert a force on the brick to establish a net force of zero. This force from the electrons is created from the "spring-like" motion of the electrons on the brick when it begins to sink into the ground. The atoms in the ground will be squished together, and because electron repulsion grows stronger as electrons are closer, the atoms will repel each other and create a "spring-like" force on the brick. Once an equilibrium of forces is established, the molecular scale of the brick will look something like this:

Thus, when the brick is pushed forward, it will have to quite literally make the ground sink to make way for its motion. The force that the atoms in the path ahead exert on the brick is what we know as friction and accounts for the reason why friction is dependent on the normal force.

Understanding Work Done by Friction

As we know, the equation for work is as follows:

[math]\displaystyle{ W = Fd }[/math] (for constant forces and one dimensional motion)

When friction is brought into the equation therefore, we get:

[math]\displaystyle{ W = fd }[/math]

We therefore should theoretically be able to calculate the work done by friction. However, we can observe an anomaly when we take into account the change in internal energy. Imagine a block moving at a constant velocity. Since the velocity is constant, the net force should be zero. If only an applied force and friction acts on the block, then the forces are equal.

[math]\displaystyle{ \Sigma {F} = 0 = {F}_{app} - f }[/math]

[math]\displaystyle{ {F}_{app} = f }[/math]

This means that if we move an object a distance d, then the total energy change of the system is zero since the forces are equal and d is the same variable in both instances:

[math]\displaystyle{ \Delta {E}_{sys} = 0 = {F}_{app} d - fd }[/math]

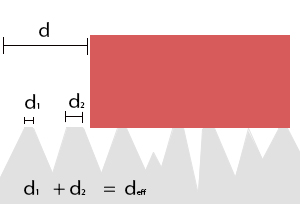
However, in a real world scenario, we observe that the temperature of the block increases as the block moves along the surface. According to our equations however, this cannot be possible since the net energy change is zero. The block moves at constant velocity which means that there is no kinetic energy change and no energy is transferred from outside the system. How is this possible? Looking at the block on a micro scale, it happens that the ground is actually not a perfect smooth surface. Instead, all surfaces have "teeth and gaps" that make it so that the block is not always in contact with the floor.

Applying this observation to our equations, the distance the apply force acts on the block stays the same; however, the distance that the frictonal force is applied on is drastically reduced. Therefore, our new equation for work (assuming constant forces) is:

[math]\displaystyle{ \Delta {E}_{sys} = {F}_{app} d - f{d}_{eff} }[/math] where [math]\displaystyle{ {d}_{eff} \lt d }[/math]

Since kinetic energy remains constant, we can conclude that:

[math]\displaystyle{ \Delta {E}_{sys} = \Delta {E}_{int} }[/math]

Now, our internal energy change is accounted for which shows why our temperature change exists.

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A 100Kg box is placed on a flat table. The box does not move. The coefficient of static friction [math]\displaystyle{ {μ}_{s} = {.25} }[/math] and the coefficient of kinetic friction [math]\displaystyle{ {μ}_{k} = {.15} }[/math]. Find the force of friction [math]\displaystyle{ {F}_{s} }[/math].

Solution:

Since the box does not move, there is only static friction. The normal force is equivalent to the force due to gravity: [math]\displaystyle{ {F}_{N} = {F}_{g} = {100}{g} }[/math]. The static friction can be found by: [math]\displaystyle{ {F}_{s} = {μ}_{s}{F}_{N} }[/math]

[math]\displaystyle{ {F}_{s} = {.25}*{100}*{9.8} = {245.25} }[/math]

Middling

A cart of mass 3Kg moves across a track pushed by a fan which exerts [math]\displaystyle{ {F} = \lt 3,0,1\gt }[/math]N with an initial velocity [math]\displaystyle{ {v}_{i} = \lt 1,0,1\gt \frac{{m}}{{s}} }[/math] . Find the required coefficient of kinetic friction [math]\displaystyle{ {μ}_{k} }[/math] needed to bring the cart to a stop in 10 seconds.

Solution:

Use the momentum principle: [math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} }[/math] and [math]\displaystyle{ {F}_{f} = {μ}_{k}{N} }[/math]

The final velocity must be 0. The initial velocity, initial force, and time are given.

[math]\displaystyle{ 0- \lt 3,0,3\gt = {F}_{net}*{10s} }[/math]

[math]\displaystyle{ {F}_{net} = \lt -0.3,0,-0.3\gt }[/math]

[math]\displaystyle{ {F}_{net} = {F} - {F}_{f} }[/math]

[math]\displaystyle{ \lt -0.3,0,-0.3\gt = \lt 3,0,1\gt - {F}_{f} }[/math]

[math]\displaystyle{ {F}_{f} = \lt 3.3,0,1.3\gt }[/math]

[math]\displaystyle{ {F}_{f} = \lt 3.3,0,1.3\gt = {μ}_{k}{N} }[/math]

[math]\displaystyle{ {N} = {3Kg} * {\lt 0,9.8,0\gt } = \lt 0,29.43,0\gt }[/math]

[math]\displaystyle{ {μ}_{k} = \frac{{F}_{f}}{{N}} = \frac{{\lt 3.3,0,1.3\gt }}{{0,29.43,0}} }[/math]

Difficult

Two blocks are stacked on top of one another on a frictionless surface. Block A is stacked on top of Block B. Block A has a mass of 2 Kg while Block B has a mass of 4 Kg. The coefficient of friction between the blocks is [math]\displaystyle{ {μ}_{s} = .35 }[/math]. Find the maximum amount of force that can be applied to Block A so that the blocks stay together.

Solution:

Momentum Principle:

[math]\displaystyle{ {p}_{f} - {p}_{i} = {F}_{net}{dt} }[/math]

We need to find the force of friction at its maximum to find the maximum amount of force that can be exerted on Block A. [math]\displaystyle{ {F}_{f} = {μ}_{s}{N} }[/math]

Forces on Block A:

[math]\displaystyle{ {F}_{A} - {F}_{f} }[/math]

Forces on Block B:

[math]\displaystyle{ {F}_{f} }[/math]

Since we want the blocks to move together, they must therefore have the same acceleration.

[math]\displaystyle{ {F}_{A} - {F}_{f} = {2 Kg} * {a} }[/math]

[math]\displaystyle{ {F}_{f} = {4 Kg} * {a} }[/math]

[math]\displaystyle{ {F}_{A} - {F}_{f} = {2 Kg} * {a} }[/math]

Since they have the same acceleration, we can use the acceleration to solve for the force applied.

[math]\displaystyle{ {a} = \frac{{F}_{A} - {F}_{f}}{{2 Kg}} }[/math]

[math]\displaystyle{ {a} = \frac{{F}_{f}}{{4}} }[/math]

[math]\displaystyle{ \frac{{F}_{A} - {F}_{f}}{{2 Kg}}= \frac{{F}_{f}}{{4 Kg}} }[/math]

[math]\displaystyle{ {F}_{A}= \frac{{3}}{{2}}{F}_{f} }[/math]

[math]\displaystyle{ {F}_{A}= \frac{{3}}{{2}} * {.35}*{6Kg}*{9.8} = {30.87} }[/math] N

Connectedness

Friction is an important topic to understand because it has many industrial implications. Since friction can cause increases in temperature when objects move, engineers who work with moving objects must understand and account for friction to ensure systems work properly. For example, car engines must have proper oil and lubricants to prevent parts from scraping together and wearing down. Mechanical engineers, aerospace engineers, and civil engineers must deal with friction and its impacts every day!

See also

External links

Internet resources on this topic

Hyper Physics: http://hyperphysics.phy-astr.gsu.edu/hbase/frict.html#fri

PHET Simulation: https://phet.colorado.edu/en/simulation/friction

References

[1] Serway, Raymond A., and John W. Jewett. Physics for Scientists and Engineers. Boston, MA: Cengage Brooks/Cole, 2014. Print.

[2] Sherwood, Bruce A. Matter & Interactions. By Ruth W. Chabay. 4th ed. Vol. 1. N.p.: John Wiley & Sons, 2015. 45-50. Print. Modern Mechanics.