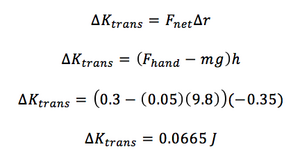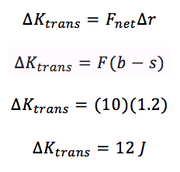Point Particle Systems

This page describes the point particle system model.

The Main Idea

The point particle system model is a model for physical systems in which multi-dimensional bodies of matter are treated as though they exist entirely at a single point in space. Usually, the point chosen for for a body is its center of mass. Objects that are modeled as single points are called particles. A particle system's mass is the same as the system's true mass, but it no longer occupies a volume. Point particle systems are simplified models; they neglect information regarding the mass distribution of a body in order to simplify the calculations necessary mathematical problems. This is in contrast to Real Systems, which are systems modeled so that all information about mass distribution is retained. Certain types of problems can be correctly solved using point particle systems because of certain properties of the center of mass.

A Mathematical Model

When a body is modeled as a point at its center of mass, some of its properties are the same as they would be if the entire mass distribution were taken into account. The following are several important such properties:

1. Inertia
2. Linear Momentum
3. Translational Kinetic Energy
4. Potential Energy due a uniform force field
5. Net Force due to a uniform force field
6. Acceleration due to a net force

Examples

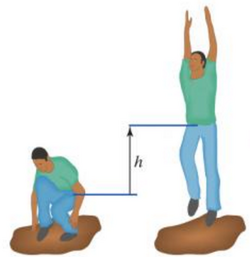
Jumper Model

A person jumps straight up in the air from a crouching position. Their center of mass moves h, or 2 m. Their total mass, m is equal to 60 kg. Find the velocity of the center of mass of the jumper. When the jumper jumps, the normal force of the ground is equal to 2x the force of gravity.

To make this problem simpler, use the center of mass of the person to collapse the whole system to one point.

Imagine the jumper's center of mass as a point, and it moves up 2 m.

Remember, , and . We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore,

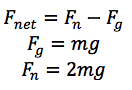
Steps:

Notice that the initial translational kinetic energy is 0, as the person is initially at rest. When worked out, the v = 6.26 m/s.

The final translational kinetic energy can be used for further calculations if one was to calculate the total change in energy of the real system. These calculations would allow you to find the change in various forms of internal energy, such as heat energy or chemical energy.

---

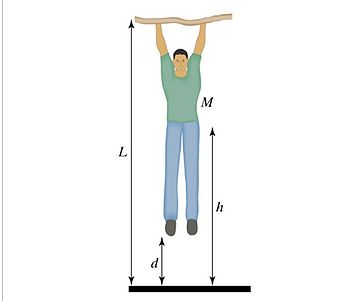
Another example that the point particle system can be applied to is someone hanging motion-less and then jumping down into a crouch position.

Looking at the system as a point particle system, you can look at the initial and final states of the man in order to find the change in energy. We are going to again use a formula for work,

In order to find the speed just before your feet touch the ground, you can set an equation as the following:

The equation for the point particle system ∆E= ∆K=Work can be applied in order to find different variables asked for in a problem.

Remember that if the man does not move, then the work done by the man will be 0 joules, because there is no displacement.

Yo-Yo Example

You pull up on a string the distance d, 0.2 m, with a force, F, 0.3 N. The yo-yo falls a distance h, 0.35 m. The mass of the yo-yo, m, is 0.05 kg. What is the change in translational kinetic energy?

For this example, the Fnet is equal to the force of your hand and the gravitational force of the earth. Delta r is equal to the movement of the yo-yo down, h.

Steps:

This information could be used to solve for the extended system, which would include the work done by your hand and the earth, as well as rotational kinetic energy.

Spring in a Box Example

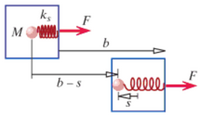
Suppose a thin box contains a ball of clay with the mass M, 2 kg, connected to a relaxed spring, with a stiffness ks, 1.2. The masses of the box and the spring are negligible. It is initally at rest, and then a constant force of F, or 10 N. The box moves a distance b, 1.5 m, and the spring stretches a distance s, 0.3 m, so that the clay sticks to the box. What is the translational kinetic energy of the box?

For the point particle system, the center of mass is the clay because the other masses are negligible. Therefore, delta r is equal to b-s, or 1.2 m. The only force acting on is F in the +x direction.

Steps:

This information could then be used for the extended system. In this example, the extended system would also include the work done by the force F, the potential energy of the spring,as well as any other internal energies.

Connectedness

1. How is this topic connected to something that you are interested in?

I find the entire realm of physics fascinating, and I find it interesting how physicists are constantly coming up with new ways to solve problems and use formulas. The point particle system is a perfect example of that. It can turn a complicated force problem into something easy to approve. I also find it interesting how you can find other forms of energy, such as chemical energy, by using point particle and real systems. Something so small and seemingly unattainable can be found using this method.

1. How is it connected to your major?

I am majoring in Materials Science and Engineering, and there are many ways all different types of physics can be used in MSE. The engineering of materials, specifically being able to calculate the amount and types of energy (and thus the cost) to produce something is absolutely crucial. Point particle systems can make this easier to do, while also adding precision to the calculations.

1. An interesting industrial application

As seen in the above examples, there are many real life applications to point particle systems, such as the energy in a person falling, or in a yoyo. This system can also be applied to industry and manufacturing, with the use of various machines that may require gears, levers, or other objects that rotate. Using point particle and real systems, you can calculate the amount of internal energy happening in a moving machine, and therefore how much energy is lost.

See also

Further reading

For more help, a helpful page is: http://p3server.pa.msu.edu/coursewiki/doku.php?id=183_notes:pp_vs_real

A helpful video lecture: https://www.youtube.com/watch?v=T780lL5FlLg&index=41&list=PL9HgJKLOnKxedh-yIp7FDzUTwZeTeoR-Y

External links

See also Real Systems for further information on using Point Particle Systems to solve for the Real Systems.

References

Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.

Purdue Physics. https://www.physics.purdue.edu/webapps/index.php/course_document/index/phys172/1160/42/5399.

Yo-yo Clipart: https://www.clipartbest.com